B站视频“线性代数的本质”观后感

线性代数对于现代科技的重要性不言而喻，在机器学习领域也是重要的工具。最近，在B站上发现了这样的一个视频：线性代数的本质。这个视频共有十集左右，每集大约10分钟，从线性空间入手，介绍线性变换，并由此介绍矩阵的相关性质，动画做的很棒，翻译得也很好，用了几天时间零散地把几集视频看完，记录一些心得。

从线性空间和线性变换讲起

BIT的教学水平，不同的老师参差不齐。所幸的是，大一教授线性代数一课的吴惠彬老师，是一位既有深厚学问又善于教课的老师。我们所用的教材，正是吴老师主编的。和这个视频不同，教材是以线性方程组入手来介绍矩阵，而后引入到线性空间和线性变换。吴老师还曾经告诫大家，线性空间和线性变换一章较为抽象晦涩，不易理解。当然，很多年过去了，我也在研究生阶段继续修了线性代数的深入课程，如今想来，其实线性变换和矩阵的联系更为紧密一些。但是我们的教材之所以不用线性变换为引子，可能正是由于对于大一新生来说，过去十二年所受的基础教育都是操作一些看得见摸得着的数和几何体，一时难以接受线性空间这种东西吧~而也正是从这门课和高数开始，思考问题的方式和初等数学不一样了。我们更多地考察运动和极限，将具有共性的东西抽象出来，研究它们的等价性质。

而抽象这个问题，在本视频中，通过将问题聚焦在二维（偶有提及三维）平面并辅之以动画的形式避开了（所以这个视频也只能算是有趣的不严肃的科普性质）。视频从线性空间入手，首先介绍了向量和基的概念，而后引入出贯穿视频系列始终的线性变换。什么是线性变换呢？从“数”的角度来看，定义在线性空间上，满足叠加性和齐次性就是线性变换。而本视频则从“形”的角度出发（注意，这也是本视频贯穿始终的指导思想：用“形”来思考），给出了下面两个条件：

• 变换前后原点不动
• 变换前后平行等距线仍然保持平行等距（但是距离值可能会变）。

线性变换与矩阵的关系

视频在阐述线性变换和矩阵关系的时候一带而过，不是很清楚（所以还是要去看严肃的教材啊）。下面是我写的一个补充说明。这也是整个视频系列的基础。

在由一组基向量$\alpha_i, i = 1,2,\dots,n$张成的线性空间$\mathcal{V}$上，任何一个向量$v$都可以表示为这组基的线性组合，也就是

$$v = \sum_{i=1}^{n}k_i\alpha_i$$

则线性变换$\mathcal{T}$对$v$作用之后，有，

$$u = \mathcal{T}(v) = \mathcal{T}(\sum_{i=1}^{n}k_i\alpha_i)$$

根据线性变换的叠加性，有，

$$u = \sum_{i=1}^{n}k_i\mathcal{T}(\alpha_i)$$

设$\alpha_i$经过线性变换$\mathcal{T}$作用后，变换为$\beta_i$，那么，

$$u = \sum_{i=1}^{n}k_i\beta_i$$

也就是说，

$$u = \begin{bmatrix}\mathcal{T}(\alpha_1), \mathcal{T}(\alpha_2), \cdots, \mathcal{T}(\alpha_n)\end{bmatrix} \begin{bmatrix}k_1\\\\ k_2\\\\ \vdots\\\\ k_n\end{bmatrix}$$

上式说明，一个抽象的线性变换可以使用一个具体的矩阵来代表。这个矩阵的列，就是线性变换之后的那组基。

举个例子，旋转变换。如果旋转$\frac{\pi}{4}$，那么原来坐标轴方向的单位向量的$i$和$j$分别转到了$(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$和$(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$。所以描述这个线性变换的矩阵为

$$A = \begin{bmatrix}\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2}\\\\ \frac{\sqrt{2}}{2}& \frac{\sqrt{2}}{2}\end{bmatrix}$$

矩阵$A$的两列分别为变换后的基向量坐标。

矩阵乘法

那么矩阵乘法的意义也就有了，那就是对向量做线性变换。例如上面的矩阵$A$与$x = \begin{bmatrix}-1\\ 0\end{bmatrix}$相乘，就是求取向量$-1i+0j$在旋转变换之后的新坐标。这时候，$-1$和$0$就是上面推导过程中的$k_1$和$k_2$，所以，

$$Ax = -1\begin{bmatrix}\frac{\sqrt{2}}{2}\\\\ \frac{\sqrt{2}}{2}\end{bmatrix} + 0\begin{bmatrix}-\frac{\sqrt{2}}{2}\\\\\frac{\sqrt{2}}{2}\end{bmatrix}$$

而矩阵与矩阵相乘呢？只要把右边的矩阵按列分块即可。其实这是矩阵与多个向量相乘的简写形式。

所以，对于任意向量$x$，$Ax$的结果就是组成矩阵$A$的各列向量的线性组合。这个由矩阵$A$的各列张成的空间叫做矩阵的列空间。

而那些使得方程$Ax=0$成立的$x$，张成的空间为矩阵的核空间。

矩阵的秩的意义就是矩阵列空间的维数。

同时，从这个角度看来，解决多元线性方程组的过程就变成了这样一个问题：即给定代表线性变换的矩阵以及变换后的向量，求解变换前向量。这个转换如下所示：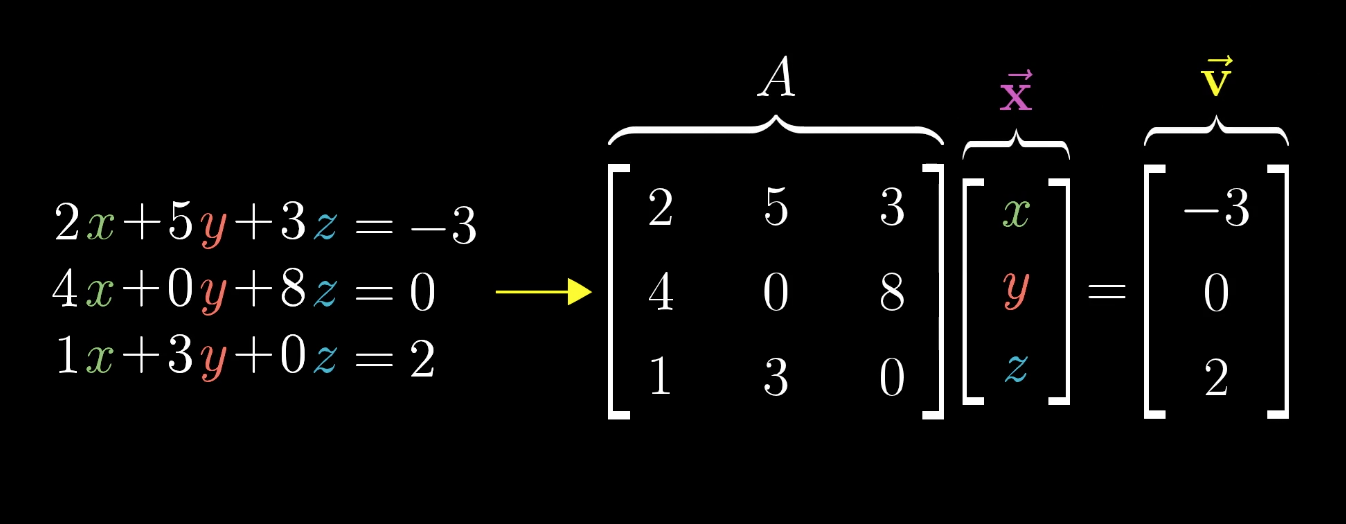

既然矩阵代表了某种线性变换，那么很自然的，可以想到，我们可以求取这个线性变换的逆变换，这个逆变换作用到$v$上，就可以得到原始的向量$x$了（而且这样的向量只有一个）！自然，这个逆变换也是有矩阵与其对应的，这个矩阵就是原矩阵的逆矩阵。那么是不是所有的矩阵都有逆矩阵呢？我们可以通过行列式来分析。

行列式

仍然考虑二维矩阵，我们已经知道它表示了二维平面上的线性变换。而矩阵行列式的意义，就表明了变换前后，单位面积的正方形被放缩的比例。如果变换之后，$i$向量跑到了$j$向量的左手边，那么需要加上负号，表明在这个变换过程中，二维平面其实进过了一次翻转。

我们已经知道，行列式为$0$的矩阵实际对线性空间进行了“降维打击”。以二维平面举例，变换之后变成了一条直线（甚至变成了一个点），也就是说对于任意给定的一个变换后向量，有这样两种情况：

• 当这个向量不在这条直线上的时候，说明没有原始向量与其对应（否则矛盾），此时原方程组无解。
• 当这个向量在这条直线上的时候，说明很多的原始向量（而且必然是无穷多）与其对应，此时原方程组有无穷多组解。

你不能将一条直线“解压缩”为原始平面，所以行列式为$0$的矩阵，不存在逆矩阵。

点积叉积和对偶性

这部分的对偶性这个概念比较玄一些，这里就不讲了。。。对于向量的点积，我们已经知道，

$$\langle v, u \rangle = \sum_{i=1}^{n}v_iu_i$$

从几何的角度看，向量的点积是将向量$u$向向量$v$的方向投影（有正负），投影长度乘上$v$的长度得到的。

按照上面矩阵乘法的思路，$u$可以看做代表一个从2维到1维的线性变换（也就是从$\mathbb{R}^2$到$\mathbb{R}$）。而根据上述矩阵变换和矩阵乘法的对应关系可知，变换后的结果就等于$v$的两个分量分别乘上两个基向量（也就是$u$的两个分量），这样我们就得到了向量点积的数值计算方法。