来呀，快活呀~

CS131-MeanShift

发表于

MeanShift最初由Fukunaga和Hostetler在1975年提出，但是一直到2000左右这篇PAMI的论文Mean Shift: A Robust Approach Toward Feature Space Analysis，将它的原理和收敛性等重新整理阐述，并应用于计算机视觉和图像处理领域之后，才逐渐为人熟知。

MeanShift是一种用来寻找特征空间内模态的方法。所谓模态（Mode），就是指数据集中最经常出现的数据。例如，连续随机变量概率密度函数的模态就是指函数的极大值。从概率的角度看，我们可以认为数据集（或者特征空间）内的数据点都是从某个概率分布中随机抽取出来的。这样，数据点越密集的地方就说明这里越有可能是密度函数的极大值。MeanShift就是一种能够从离散的抽样点中估计密度函数局部极大值的方法。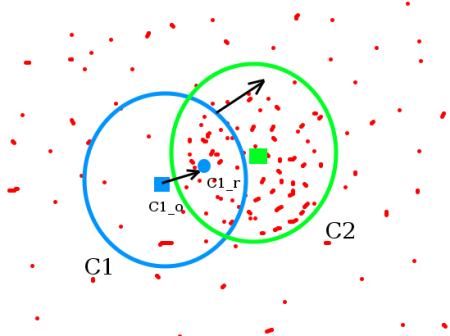
MeanShift

核密度估计

上面提到的PAMI论文篇幅较长，且数学名词较多，我不是很理解。下面的说明过程主要参考了这篇博客和这篇讲义。

注意下面的推导中$x$是一个$d$维的向量。为了书写简单，没有写成向量的加粗形式。首先，先介绍核函数（Kernel Function）的概念。如果某个$\mathbb{R}^n\rightarrow \mathbb{R}$的函数满足以下条件，就能将其作为核函数。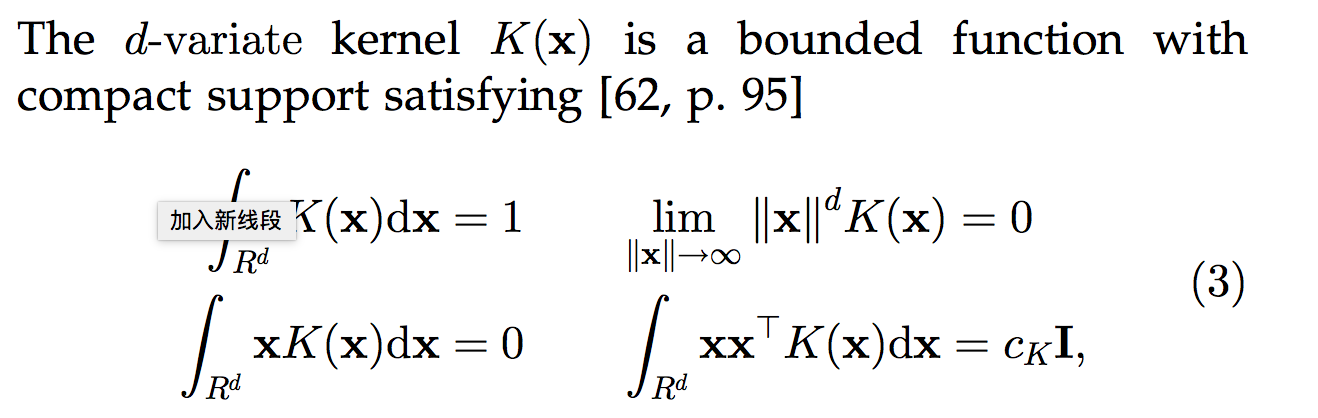
kernel

比如高斯核函数：

核密度估计是一种用来估计随机变量密度函数的非参数化方法。给定核函数$K$，带宽（bandwidth）参数$h$（指观察窗口的大小）。那么密度函数可以使用核函数进行估计，如下面的形式所示。其中，$n$是窗口内的数据点的数量。

如果核函数是放射形状且对称的（例如高斯核函数），那么$K(x)$可以写成如下的形式，其中$c_{k,d}$是为了使得核函数满足积分为$1$的正则系数。

mean shift向量

那么，原来密度函数的极值点就是使得$f(x)$梯度为$0$的点。求取$f(x)$的梯度，可以得到下式。其中$g(s) = -k^\prime(s)$。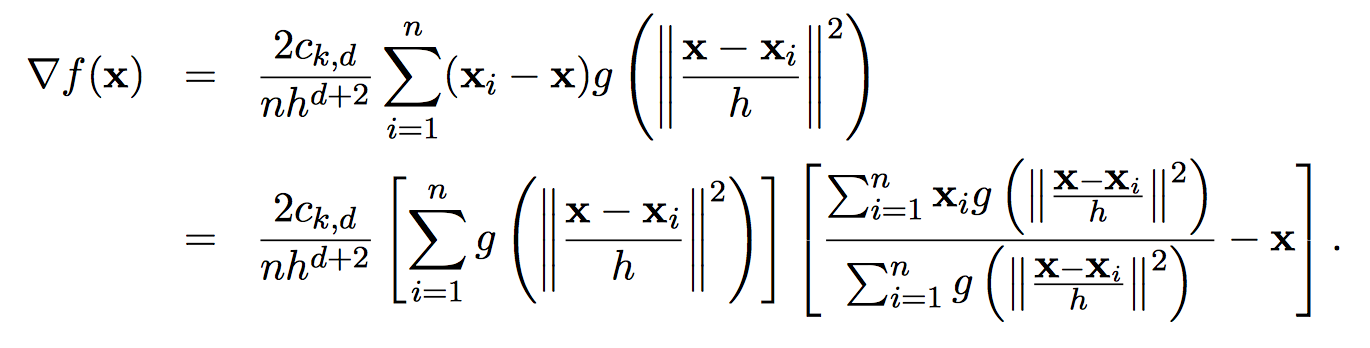
密度函数的梯度

观察后可以发现，乘积第一项连带前面的系数，相当于是使用核函数$G(x) = c_{k,d}g(\Arrowvert x\Arrowvert^2)$得到的点$x$处的密度函数估计值（差了常数倍因子）（所以对于给定的某一点$x = x_0$，这一项是定值），后面一项拿出来，定义为$m_h(x)$，称为mean shift向量。

所以说，$m_h(x)$的指向和$f(x)$的梯度是相同的。另外，从感性的角度出发。$m_h(x)$中的第一项（分式的那一大坨），相当于是在计算$x$周围窗口大小为$h$的这个领域的均值（$g(s)$是加权的系数）。所以$m_h(x)$实际上指示了局部均值和当前点$x$之间的位移。我们想要找到密度函数的局部极大值，不就应该让局部均值向着点密集的方向移动吗？

算法流程

所以，在给定初始位置$x_0$后，我们首先计算此点处的$m_h$，之后，将$x$沿着$m_h$移动即可。下面是一个简单的例子。数据点服从二维高斯分布，均值为$[1, 2]$。其中，红色菱形指示了迭代过程中mean shift的移动。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
%% generate data
mu = [1 2];
Sigma = [1 0; 0 2]; R = chol(Sigma);
N = 250;
data = repmat(mu, N, 1) + randn(N, 2)*R;
figure
hold on
scatter(data(:, 1), data(:, 2), 50, 'filled');
%% meanshift
mu0 = rand(1,2) * 5;
mu = mean_shift(mu0, 10, data);

function out = gaussian_kernel(x, sigma)
% gauss kernel, g(x) = \exp(-x^2/2\sigma^2)
out = exp(-x.*x/(2*sigma*sigma));
end

function mu = mean_shift(mu0, h, data)
% implementation of meanshift algorithm
% mu_{k+1} = meanshift(mu_{k}) + mu_{k} = \frac{\sum_i=1^n xg}{\sum_i=1^n g}
mu = mu0;
sigma = 1;    % parameter for gaussian kernel function
for iter = 1:20    
    fprintf('iter = %d, mu = [%f, %f]\n', iter, mu(1), mu(2));
    scatter(mu(1), mu(2), 50, [1,0,0], 'd', 'filled');
    offset = bsxfun(@minus, mu, data);    % offset = x-x_i
    dis = sum(offset.^2, 2);              % dis = ||x-x_i||^2
    x = data(dis < h, :);                 % neighborhood with bandwidth = h
    g = gaussian_kernel(offset(dis < h), sigma);
    xg = x.*g;
    mu_prev = mu;
    mu = sum(xg, 1) / sum(g, 1);
    if norm(mu_prev - mu, 2) < 1E-2
        break;
    end
    plot([mu_prev(1) mu(1)], [mu_prev(2), mu(2)], 'b-.', 'linewidth', 2);
end
scatter(mu(1), mu(2), 50, [1,0,0], 'd', 'filled');
end

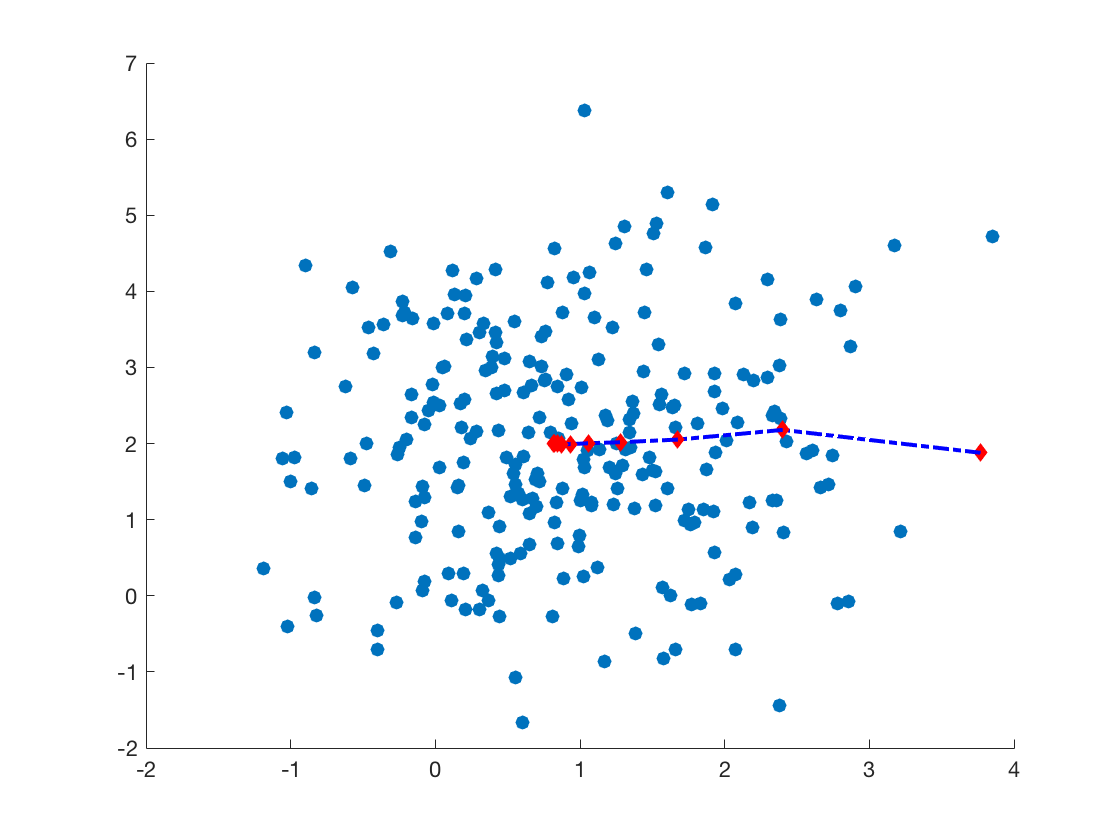
同时，我也试验了其他的kernel函数，如神似logistaic形式，效果也是相似的。

1
2
3
function out = logistic_kernel(x)
out = 1./(exp(x) + exp(-x) + 2);
end