Residuel Net是MSRA HeKaiming组的作品,斩获了ImageNet挑战赛的所有项目的第一,并荣获CVPR的best paper,成为state of the ar的网络结构。这篇文章记录了阅读最初论文“Deep Residual Learning for Image Recongnition”的重点。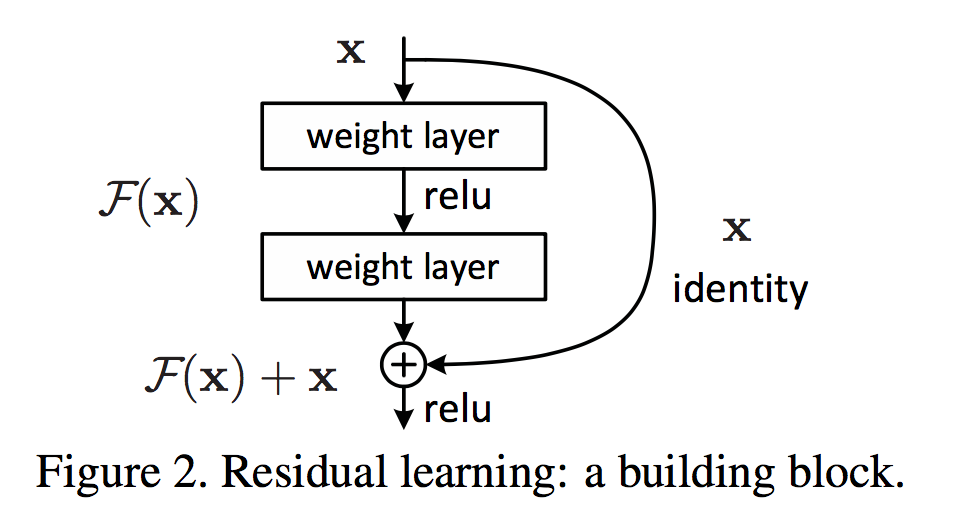
更深的网络 -> 更好的性能
在ImageNet等比赛上,大家已经发现了一个现象,就是更深的网络往往能够获得更好的成绩。从LeNet到AlexNet再到VGG Net和GoogLeNet,网络层次越来越深,然而增加网络深度在实际中遇到了很多的问题。
在序言部分,这篇论文也是首先提出了一个问题:我们只需要不断在现有结构基础上堆叠更多的layer就可以获得更好的网络吗?
Is learning better networks as easy as stacking more layers?
很明显,答案是否定的。一个问题就是梯度的消失(或爆炸)。在bp过程中,过深的网络结构会导致传导到底层的梯度变的很小(或飞升),导致训练失败。这一问题在BN层提出之后得到了一定的解决。
另一个问题是在实验过程中观测到的。通过实验,作者发现,当不断增加网络深度的时候,网络的性能会不再提升。如果再继续添加深度,网络的性能甚至会下降!下面是作者在CIFAR-10上做的实验,使用56层的网络比20层的网络,无论在训练集还是测试集上都落于下风。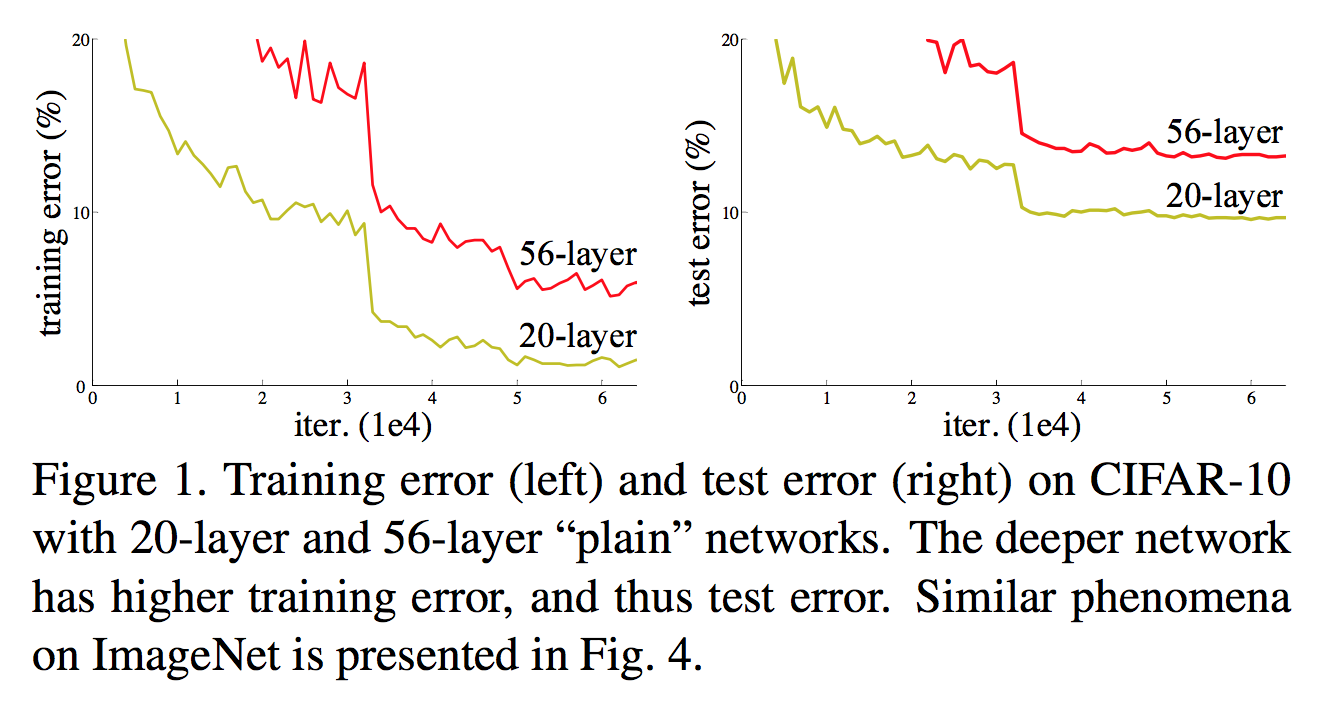
个人觉得,这个现象看上去意料之外,情理之中。并不是说56层的网络的学习能力不如20层,而是训练不同深度的神经网络的难度是不同的。作者联想到(这里的想法很好!),如果我们已经有了一个较浅的网络(shadow net),然后我们在其后面接上若干的等同映射(Identity Mapping),那么新得到的更深的网络应该是和前者有相同的表现的。这个思想实验,巧妙地说明了并不是更深的网络变坏了,而是我们现有的方法不能很好地训练更深的网络。
残差单元
也是受上面这个思想实验中的Identity Mapping的启发,作者设计了一种残差网络结构,以它为基本单元构建更深的网络,以期解决第二个问题。
使用残差单元时,我们不再让网络去直接学映射$\mathcal{H}(x)$,而是学习映射$\mathcal{F}(x) = \mathcal{H}(x) - x$。作者也简单说了为何使用这种残差结构。这种方法给要学的映射加上了一个等同映射作为参考。同时考虑极端情况,如果最优的结构真的是等同映射的话,那么学习到的$\mathcal{F}(x)$为$0$就好了。这个网络的性能起码是不输于那个浅层网络的。
应用这种残差结构就可以很容易地搭建深层网络了。使用这种技术,作者构建了多达$1000$多层的网络,同时在多项比赛中狂揽桂冠,在实践中证明了它的威力。
残差学习
从上面的介绍看出,使用残差结构后,网络不再直接学习最终的映射$\mathcal{H}$,而是这个映射和输入的残差$\mathcal{F}$。这里叫做残差学习(Residual Learning)。
神经网络可以近似任意复杂的函数(作者指出此处存疑,还是作为假设)所以,它不仅可以逼近$\mathcal{H}$,当然也可以逼近残差。这两者虽然都可以通过网络近似,但是训练难度是不同的。
上面图中的残差单元结构可以写成下面的式子,其中的$W_i$就是决定残差映射$\mathcal{F}$的参数,也是训练中要优化的东西。这里为了书写简单,省略了偏置项。
上面的式子要求$\mathcal{F}(x)$与$x$有相同的维度,如果维度不同的话,可以给输入$x$乘上一个权重参数矩阵$W_s$,做一下维度匹配。当然,即使维度相同,我们也可以乘上一个方阵$W_s$,但是这样一来,一是给网络引入了更多的参数(这样,我们的残差结构打脸效果不就打折扣了?),同时在论文中的实验部分也证明了加入这个矩阵对提升性能没用(Identity Mapping已经够用了)。
同时,在设计残差结构的时候,也不必非要像上面的图那样设计两层,完全可以设计更多(比如下面的bottleneck结构,只是别减少得只剩一层了,那样的话$\mathcal{F}$只剩一个线性映射可以学了。。。)。
ImageNet实验和比较
由此,我们可以构建残差网络。这里开始,作者通过一系列实验,来证明残差结构的优越性:更少的参数,更深的层数,更优秀的性能。
这里着重介绍作者在ImageNet上的实验结果。
作者首先对比了18层和34层plain网络和残差网络的表现,进一步验证了序言中的结论。采用普通的结构,更深的网络(34层)表现反而不如较浅的网络,而使用残差结构则没有这个问题。从下图左右的对比可以很清楚地看出这个现象。作者同时指出这一现象不大可能是由于梯度消失造成的。
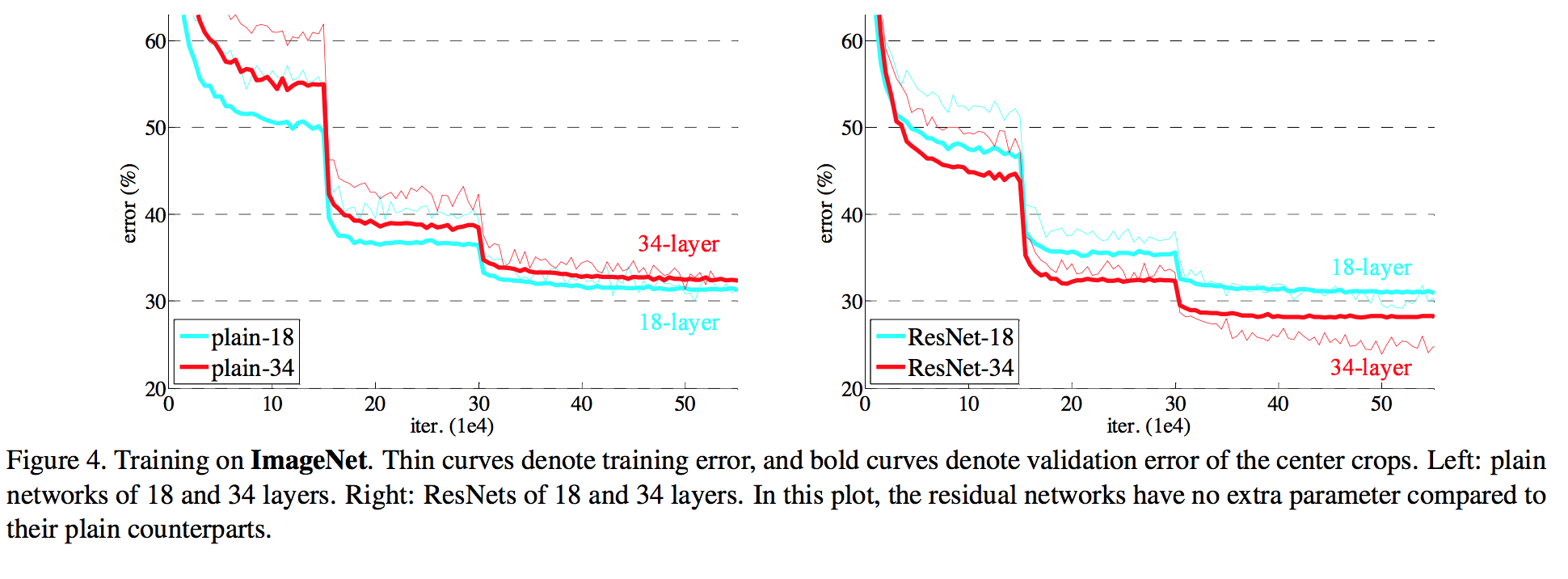
另外一个从实验中观察到的现象指出,对于18层这种较浅的网络,使用残差结构能够加快收敛速度,使得训练更加容易。
同时,对于上面提到的维度不匹配的问题,作者提出了三个解决方案并进行了对比。
- 方案A使用zero-padding的方法
- 方案B使用乘上权重矩阵的方法
- 方案C不止在维度不匹配时乘权重矩阵,而且所有的Identity Mapping都换成这种形式
实验结果表明,模型表现A<B<C。但是性能差距较小。由于C引入了很多额外的参数,所以并不使用这种方法(聚焦主要矛盾)。
Bottleneck结构
为了节省训练时间,作者提出了一种新的变形——Bottleneck结构。见下图右侧。首先将两层结构扩展为三层,最前面和最后面都是$1\times 1$的卷积核,来进行channel的变形。通过前面的$1\times 1$卷积核,将channel降下来。和$3\times 3$卷积核作用后,再用最后的$1\times 1$卷积核升上去。
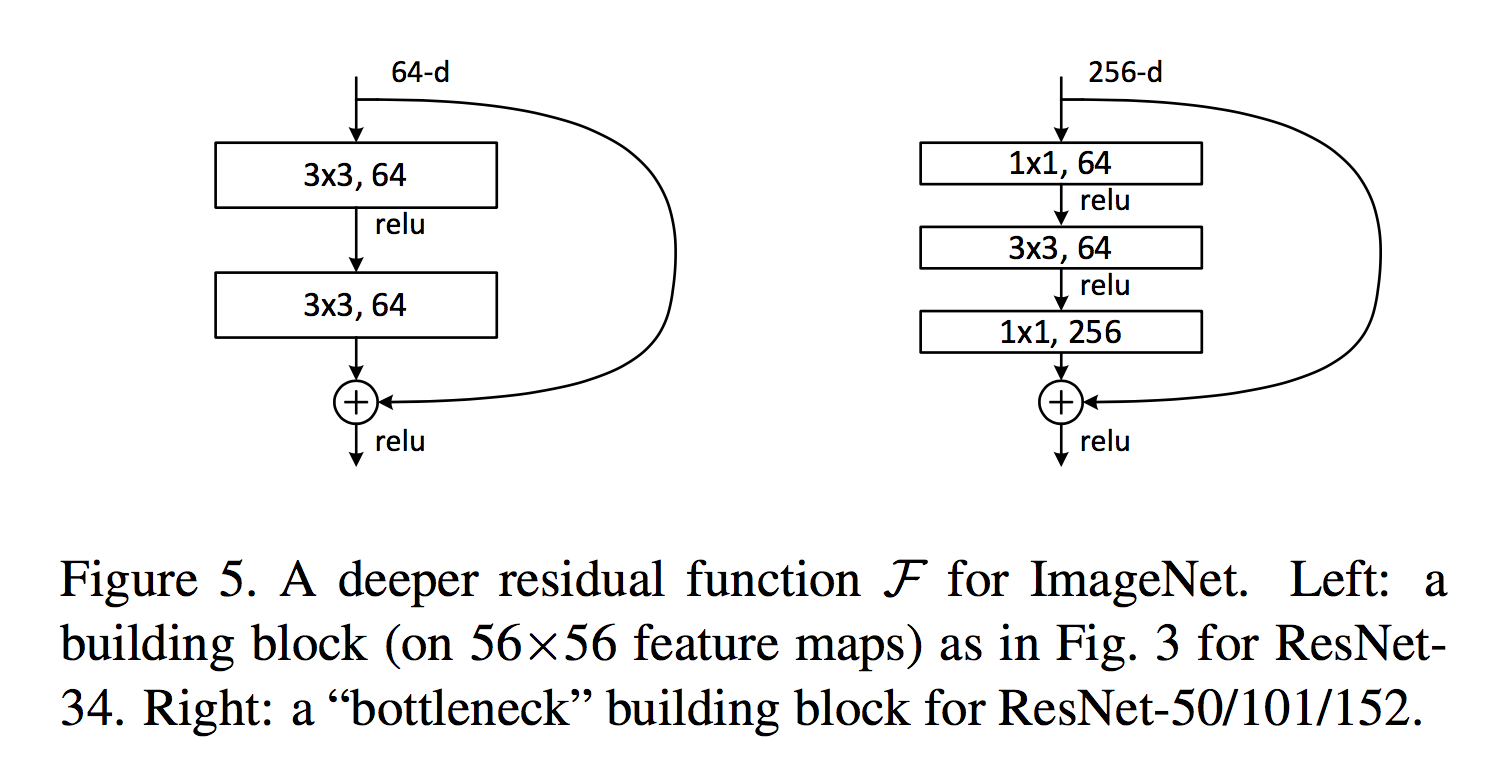
使用这一单元结构,作者构建了50层,101层和152层的深层网络,并最终取得了很好的成绩。
附录
在附录中,作者描述了在Pascal VOC和COCO目标检测和定位任务中使用Residual Net的情况。对于目标检测这个任务,后续可以参见MSRA的R-FCN那篇文章。