这篇文章是He Kaiming继最初的那篇ResidualNet的论文后又发的一篇。这篇论文较为详细地探讨了由第一篇文章所引入的Identity Mapping,结合具体实验,测试了很多不同的组合结构,从实践方面验证了Identity Mapping的重要性。同时,也试图对Identity Mapping如此好的作用做一解释。尤其是本文在上篇文章的基础上,提出了新的残差单元结构,并指出这种新的结构具有更优秀的性能。
从残差到残差
在第一篇文章中,作者创造性地提出了残差网络结构。简洁的网络结构,优异的性能,实在是一篇佳作,得到CVPR best paper实至名归。在这篇文章的开头,作者回顾了残差网络的一般结构,如下所示。其中,$x_l$和$x_{l+1}$表示第$l$个残差单元的输入和输出,$\mathcal{F}$为残差函数。
在上篇文章中,作者将$f(x)$取作ReLU函数,将$h(x)$取作Identity Mapping,即,
在这篇文章中,作者提出了新的网络结构,和原有结构比较如下。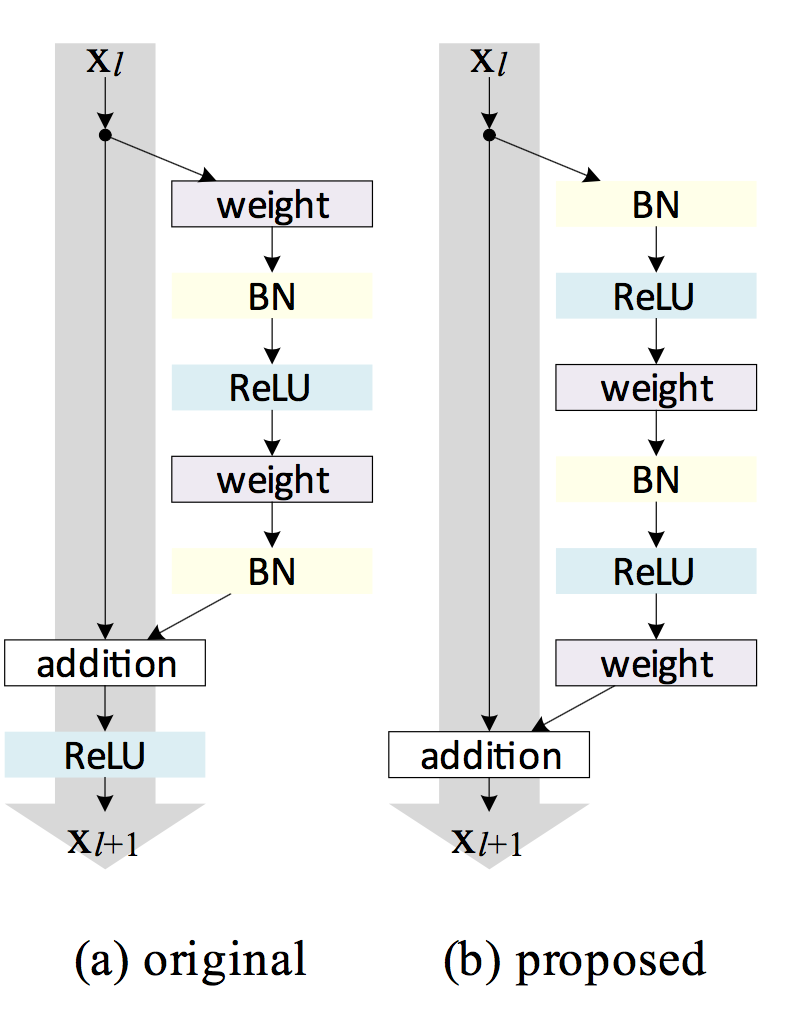
作者提出,将BN层和ReLU看做是后面带参数的卷积层的”前激活”(pre-activation),取代原先的“后激活”(post-activation)。这样就得到了上图右侧的新结构。
从右图可以看到,本单元的输入$x_l$首先经过了BN层和ReLU层的处理,然后才通过卷积层,之后又是BN-ReLU-conv的结构。这些处理过后得到的$y_l$,直接和$x_l$相加,得到该层的输出$x_{l+1}$。
利用这种新的残差单元结构,作者构建了1001层的残差网络,在CIFAR-10/100上进行了测试,验证了新结构能够更容易地训练(收敛速度快),并且拥有更好的泛化能力(测试集合error低)。
Identity Mapping: Why Always me?
作者在后面的文章中对这种新结构进行了理论分析和实验测试,试图解释Identity Mapping为何这么重要。实验部分不再多介绍了,无非就是把作者的实验配置和结果贴出来,好麻烦。。。这里只把作者的理论分析整理如下。如果想要复现坐着的工作,还是要结合论文去好好看一下实验部分。
在使用了这种新结构之后,我们有,
如果我们的网络都是由这种残差网络组成的,递归地去倒到前面较浅的某一层,则:
从上面的式子可以看出,
- 深层单元$L$的特征$x_L$可以被表示为浅层单元的特征$x_l$j加上它们之间各层的残差函数$\mathcal{F}$。
- 我们有,$x_L=x_0+\sum_{i=0}^{L-1}\mathcal{F}(x_i, W_i)$,而普通网络$x_L$和$x_l$的关系比较复杂,$x_L = \prod_{i=0}^{L-1}W_ix_0$。看上去,前者的优化应该更加简单。
计算bp的时候,有,
上式表明,由于残差单元的短路连接(shortcut),$x_l$处的梯度基本不会出现消失的情况(除非后面一项正好等于-1)。
如果不做Identity Mapping,而是乘上一个系数$\lambda$呢?作者发现这会在上面的式子上出现$\lambda^k$的形式,造成梯度以指数规律vanish或者爆炸。同样的,如果乘上一个权重,也会有类似的效应。
所以,Identity Mapping是坠吼的!
花式跑实验
论文的后半部分,作者开始花式做实验,调研了很多不同的结构,具体实验方案和对比结果可以参看原论文。这里不再罗列了。附上自己用PyTorch实现的164层ResNet在CIFAR10上的训练代码:Gist Code: ResNet-164 training experiment on CIFAR10 using PyTorch。
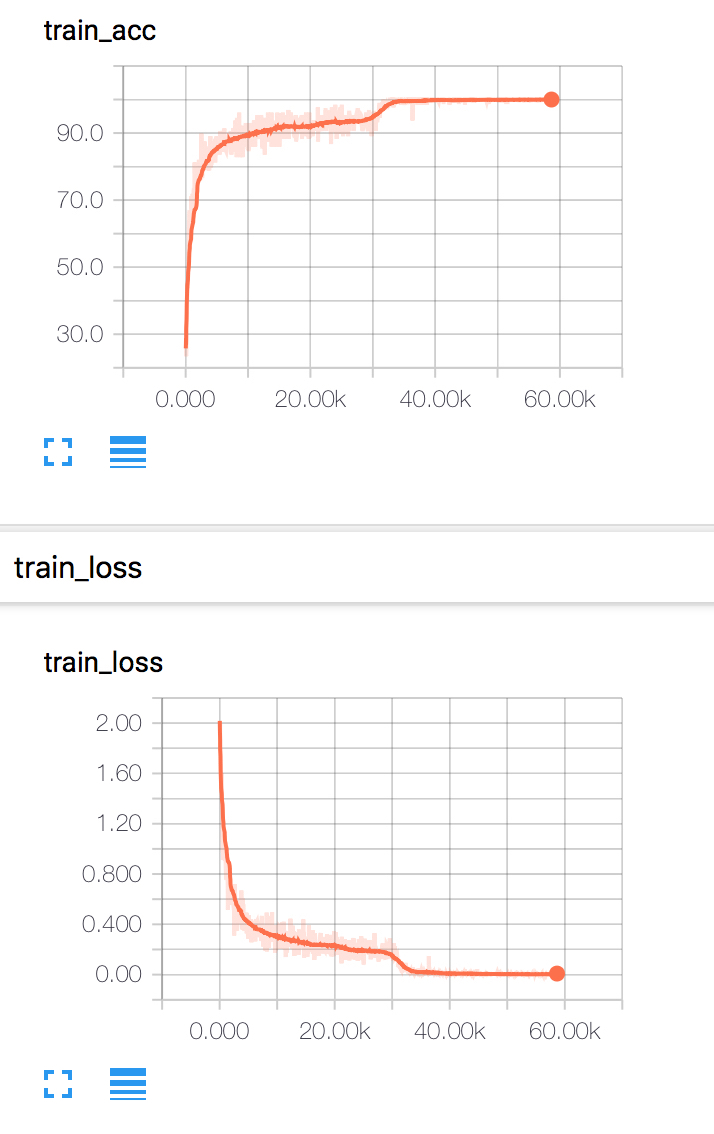
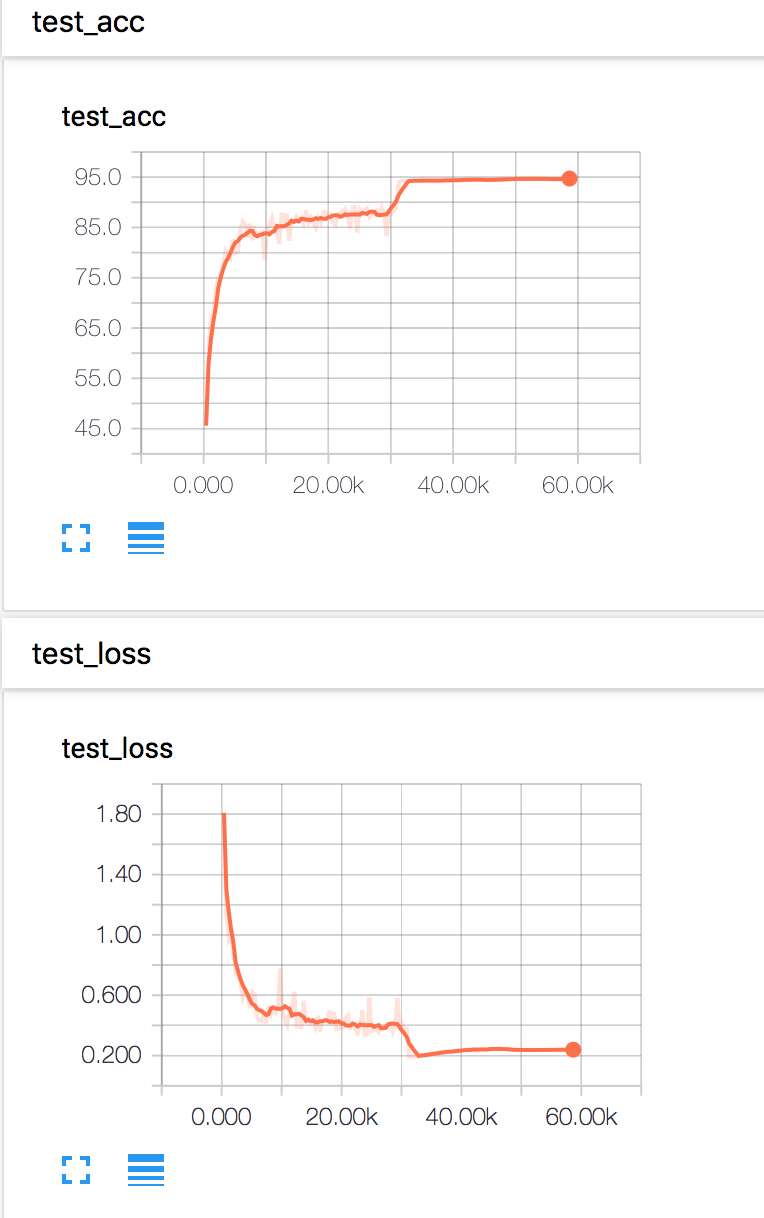
下面的可视化结果由DMLC/tensorboard实现。图上在$30K$次迭代附近有明显的性能提升,对应于学习率的调整,变为原来的$0.1$。