来呀，快活呀~

Caffe中的底层数学计算函数

发表于

Caffe中使用了BLAS库作为底层矩阵运算的实现，这篇文章对mathfunction.hpp 文件中的相关函数做一总结。我们在自己实现layer运算的时候，也要注意是否Caffe中已经支持了类似运算，不要从scratch开始编码，自己累点不算啥，CPU/GPU的运算能力发挥不出来，更别说自己写的代码也许还是错的，那就尴尬了。。。
一卡一栋楼，双卡灭地球，三卡银河系，四卡创世纪

BLAS介绍

以下内容参考BLAS wiki页面整理。这里不涉及BLAS的过多内容，只为介绍Caffe中的相关函数做一过渡。

BLAS的全称是基础线性代数子程序库（Basic Linear Algebra Subprograms），提供了一些低层次的通用线性代数运算的实现函数，如向量的相加，数乘，点积和矩阵相乘等。BLAS的实现根绝硬件平台的不同而不同，常常利用了特定处理器的硬件特点进行加速计算（例如处理器上的向量寄存器和SIMD指令集），提供了C和Fortran语言支持。

不同的厂商根据自己硬件的特点，在BLAS的统一框架下，开发了自己的加速库，比如AMD的ACML（已经不再支持），Intel的MKL，ATLAS和OpenBLAS。其中后面的三个均可以在Caffe中配置使用。

在BLAS中，实现了矩阵与矩阵相乘的函数gemm（GEMM: General Matrix to Matrix Multiplication）和矩阵和向量相乘的函数gemv，这两个数学运算的高效实现，关系到整个DL 框架的运算速度。下面这张图来源于Jia Yangqing的博士论文。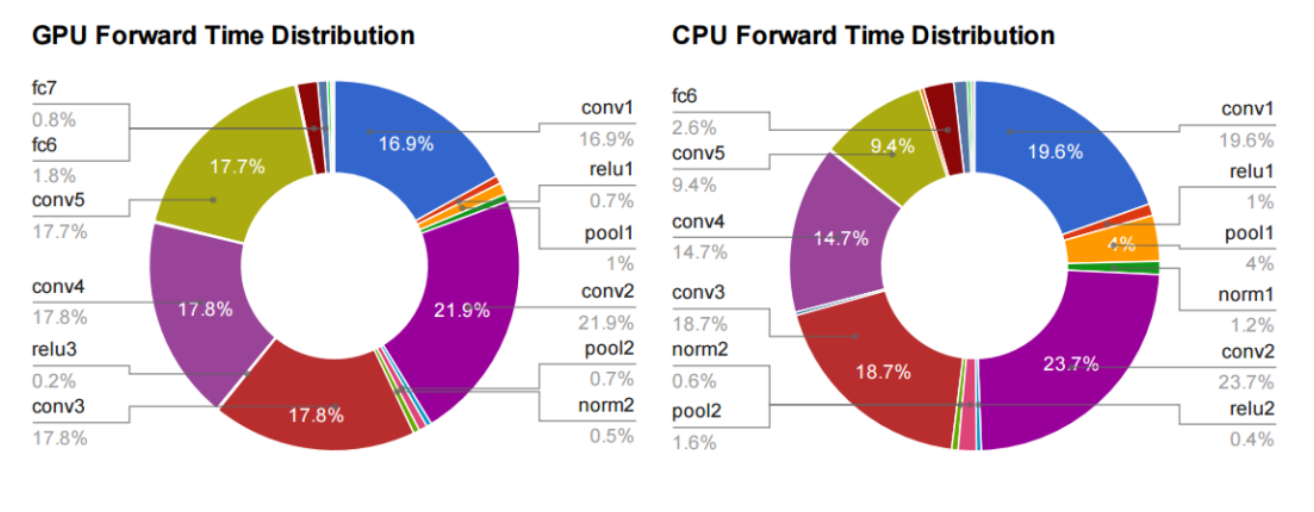
前向计算中的典型时间分布

可以看到，在前向计算过程中，无论是CPU还是GPU，大量时间都花在了卷积层和全连接层上。全连接层不必多说，就是一个输入feature和权重的矩阵乘法。卷积运算也是通过矩阵相乘实现的。因为我们可以把卷积核变成一列，和相应的feature区域做相乘（如下图，这部分可以看一下Caffe中im2col部分的介绍和代码）。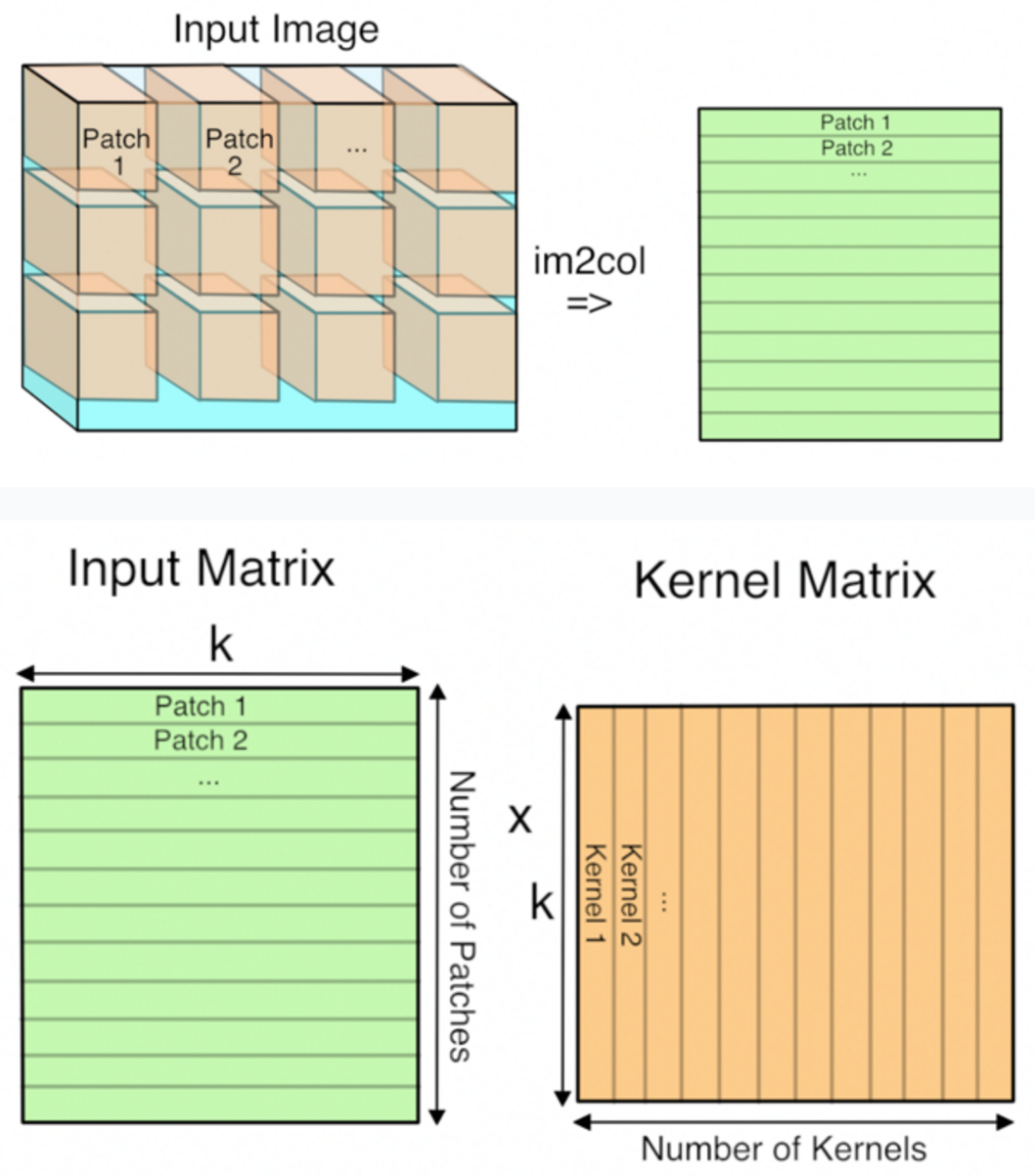
im2col的原理

对于BLAS和GEMM等对DL的作用意义，可以参见这篇文章Why GEMM is at the heart of deep learning的分析。上面的图也都来源于这篇博客。

矩阵运算函数

矩阵运算函数在文件math_functions.hpp中可以找到。其中的函数多是对BLAS相应API的包装。这部分内容主要参考了参考资料[1]中的内容。谢谢原作者的整理。

矩阵与矩阵，矩阵与向量的乘法

函数caffe_cpu_gemm()是对BLAS中矩阵与矩阵相乘函数gemm的包装。与之对应的caffe_cpu_gemv()是对矩阵与向量相乘gemv函数的包装。以前者为例，其实现代码如下：

1
2
3
4
5
6
7
8
9
10
template<>
void caffe_cpu_gemm<float>(const CBLAS_TRANSPOSE TransA,
    const CBLAS_TRANSPOSE TransB, const int M, const int N, const int K,
    const float alpha, const float* A, const float* B, const float beta,
    float* C) {
  int lda = (TransA == CblasNoTrans) ? K : M;
  int ldb = (TransB == CblasNoTrans) ? N : K;
  cblas_sgemm(CblasRowMajor, TransA, TransB, M, N, K, alpha, A, lda, B,
      ldb, beta, C, N);
}

可以看到，这个函数是对单精度浮点数（Single Float）的模板特化，在函数内部调用了BLAS包中的cblas_sgemm()函数。其功能是计算C = alpha * A * B + beta * C。参数的具体含义可以查看BLAS的相关文档。

矩阵/向量的加减

下面的函数都是将X指针所指的数据作为src，将Y指针所指的数据为dst。同时，第一个参数统一是向量的长度。

  • caffe_axpy(N, alpha, x, mutable y)实现向量加法Y = alpha * X + Y。
  • caffe_axpby(N, alpha, x, beta, mutable y)实现向量加法Y = alpha * X + beta * Y

这两个函数的用法可以参见欧氏距离loss函数中的梯度计算：

1
2
3
4
5
6
7
caffe_cpu_axpby(
    bottom[i]->count(),              // count
    alpha,                              // alpha
    diff_.cpu_data(),                   // a
    Dtype(0),                           // beta
    bottom[i]->mutable_cpu_diff());  // b
}

其中，bottom[i]->count()给定了blob的大小，也就是向量的长度。alpha实际是由顶层top_blob传来的loss_weight，也即是*top_blob->cpu_diff()/batch_size。由于是直接将加权后的diff直接赋给bottom_blob的cpu_diff，所以，将beta赋值为0。

内存相关

和C语言中的memset()和memcpy()类似，Caffe内也提供了对内存的拷贝与置位。使用方法也和两者相似：

  • caffe_copy(N, x, mutable y)实现向量拷贝。源地址和目标地址服从上小节的约定。
  • caffe_set(N, alpha, mutable x)实现向量的置位，将向量分量填充为值alpha。

查看其实现可以知道，这里Caffe中直接调用了memset()完成任务。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
template <typename Dtype>
void caffe_set(const int N, const Dtype alpha, Dtype* Y) {
  if (alpha == 0) {
    memset(Y, 0, sizeof(Dtype) * N);  // NOLINT(caffe/alt_fn)
    return;
  }
  for (int i = 0; i < N; ++i) {
    Y[i] = alpha;
  }
}

// 模板的特化
template void caffe_set<int>(const int N, const int alpha, int* Y);
template void caffe_set<float>(const int N, const float alpha, float* Y);
template void caffe_set<double>(const int N, const double alpha, double* Y);

而caffe_copy()中则是直接实现了CPU和GPU的功能。注意到下面代码中调用cudaMemcpy()的时候，使用了参数cudaMemcpyDefault。通过查阅文档，这个变量的含义是cudaMemcpyDefault: Default based unified virtual address space。通过它，我们可以无需知道源地址和目标地址是否在CPU内存或者GPU内存上而分别处理，减少了代码负担。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
template <typename Dtype>
void caffe_copy(const int N, const Dtype* X, Dtype* Y) {
  if (X != Y) {
    if (Caffe::mode() == Caffe::GPU) {
#ifndef CPU_ONLY
      // NOLINT_NEXT_LINE(caffe/alt_fn)
      CUDA_CHECK(cudaMemcpy(Y, X, sizeof(Dtype) * N, cudaMemcpyDefault));
#else
      NO_GPU;
#endif
    } else {
      memcpy(Y, X, sizeof(Dtype) * N);  // NOLINT(caffe/alt_fn)
    }
  }
}

所谓的unified virtual address（UVA）就是下图这个意思（见P2P&UVA）。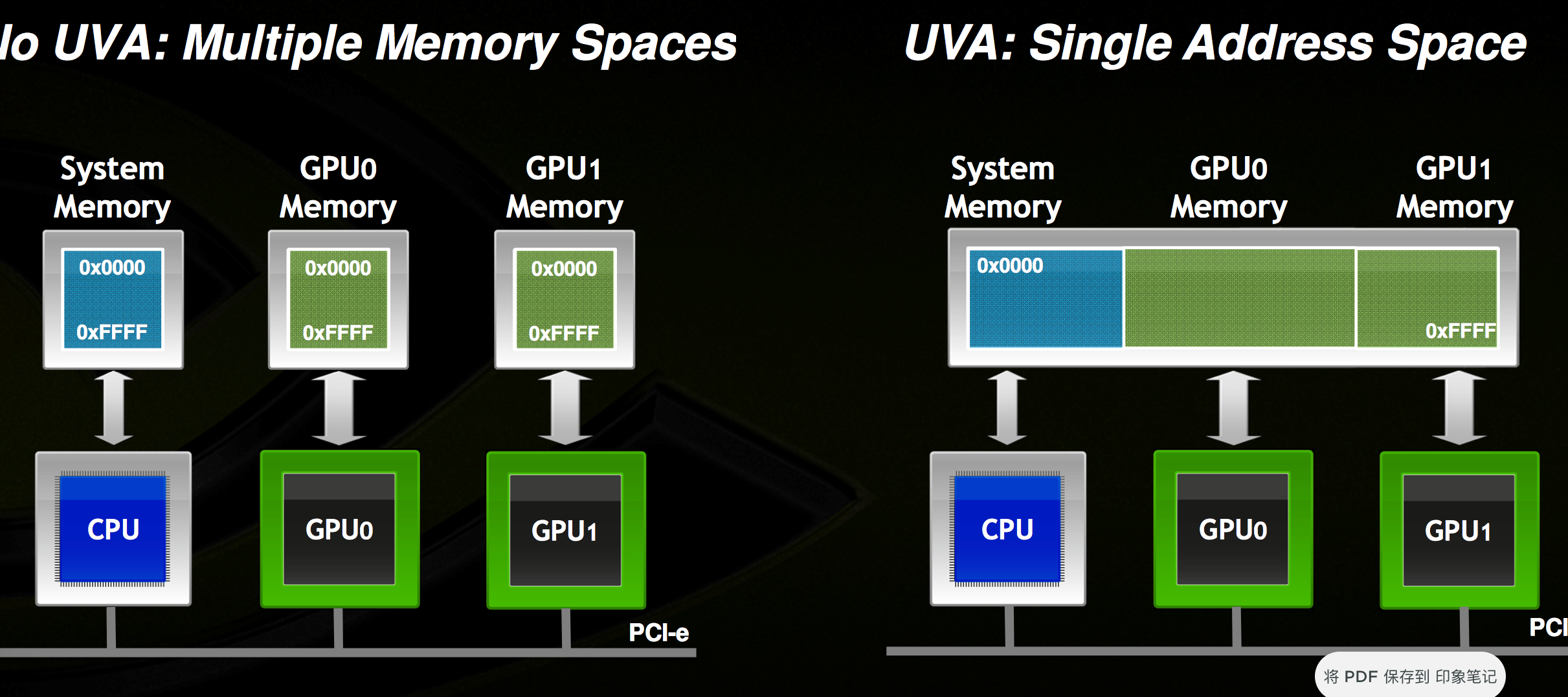
UVA图示

有了这个东西，可以将内存和GPU显存看做一个统一的内存空间。CUDA运行时会根据指针的值自动判断数据的实际位置。这样一来，简化了编程者的工作量，如下所示：
How to use UVA

其使用条件如下：
UVA Requirement

向量逐元素运算

  • caffe_add(N, a, b, y)函数实现Y[i] = a[i] + b[i]。
  • caffe_sub, caffe_div, caffe_mul同理。
  • caffe_exp, caffe_powx, caffe_abs, caffe_sqr, caffe_log相似，这里只将caffe_exp()的实现复制如下：
1
2
3
4
5
// 又是模板特化
template <>
void caffe_exp<float>(const int n, const float* a, float* y) {
  vsExp(n, a, y);   // 返回 y[i] = exp(a[i])
}
  • caffe_scal实现向量的数乘。这个函数常常用在loss_layer中计算反传的梯度，常常要乘上一个标量loss_weight。
  • caffe_add_scalar实现向量每个分量与标量相加。

GPU版本

相应地，和基于BLAS的CPU数学计算函数相似，各GPU版本的函数声明也放在了math_functions.hpp中，而相应的实现代码在math_functions.cu中。

随机数产生器

Caffe中还提供了若干随机数产生器，可以用来做数据（如权重矩阵）的初始化等。

这里，Caffe提供饿了均匀分布（uniform），高斯分布（gaussian），伯努利分布（bernoulli）的实现。这里就不再详述，使用函数caffe_rng_distribution_name即可。

参考资料

【1】seven-first 的博客