来呀，快活呀~

CS131-光流估计

发表于

光流法是通过检测图像像素点的强度随时间的变化进而推断出物体移动速度及方向的方法。由于成像物体与相机之间存在相对运动，导致其成像后的像素强度值不同。通过连续观测运动物体图像序列帧间的像素强度变化，就可以估计物体的运动信息。

是你让我的世界从那刻变成粉红色 划掉。。。
OpticalFlow可视化

光流的计算

光流（Optical Flow），是指图像中像素强度的“表象”运动。这里的表象运动，是指图像中的像素变化并不一定是由于运动造成的，还有可能是由于外界光照的变化引起的。

光流估计就是指利用时间上相邻的两帧图像，得到点的运动。满足以下几点假设：

  • 前后两帧点的位移不大（泰勒展开）
  • 外界光强保持恒定。
  • 空间相关性，每个点的运动和他们的邻居相似（连续函数，泰勒展开）

其中第二条外界光强保持恒定，可以从下面的等式来理解。
光照强度保持恒定图解

在相邻的两帧图像中，点$(x,y)$发生了位移$(u,v)$，那么移动前后两点的亮度应该是相等的。如下：

从这个式子出发，我们将其利用Taylor展开做一阶线性近似。其中$I_x$, $I_y$, $I_t$分别是Image对这几个变量的偏导数。

上面两式联立，可以得到，

上式中，$I_x$, $I_y$可以通过图像沿$x$方向和$y$方向的导数计算，$I_t$可以通过$I(x,y,t)-I(x,y,t-1)$计算。未知数是$(u,v)$， 正是我们想要求解的每个像素在前后相邻两帧的位移。

这里只有一个方程，却有两个未知数（实际是$N$个方程，$2N$个未知数，$N$是图像中待估计的像素点的个数，但是我们通过矩阵表示，将它们写成了如上式所述的紧凑形式），所以是一个不定方程。我们需要找出其它的约束求解方程。

上面就是光流估计的基本思想。下面一节介绍估计光流的一种具体方法：Lucas-Kanade方法

L-K方法

上述式子虽然给出了光流估计的思路，但是还是没有办法解出位移量。L-K方法依据相邻像素之间的位移相似的假设，通过一个观察窗口，将窗口内的像素点的位移看做是相同的，建立了一个超定方程，使用最小二乘法进行求解。下面是观察窗口为$5\times 5$的时候，建立的方程。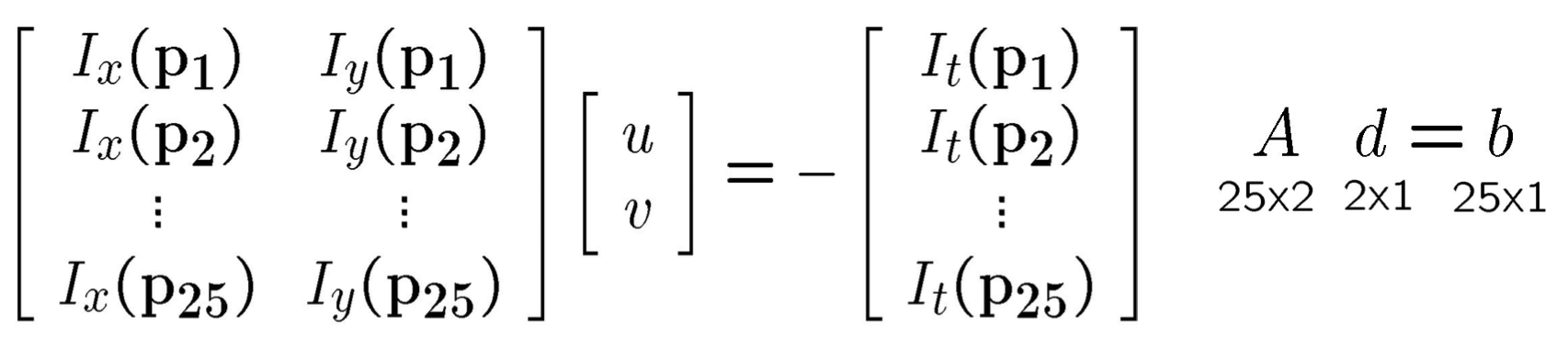
L-K方程

使用最小二乘法求解，可以得到如下的式子，求和号代表是对窗口内的每一个像素点求和。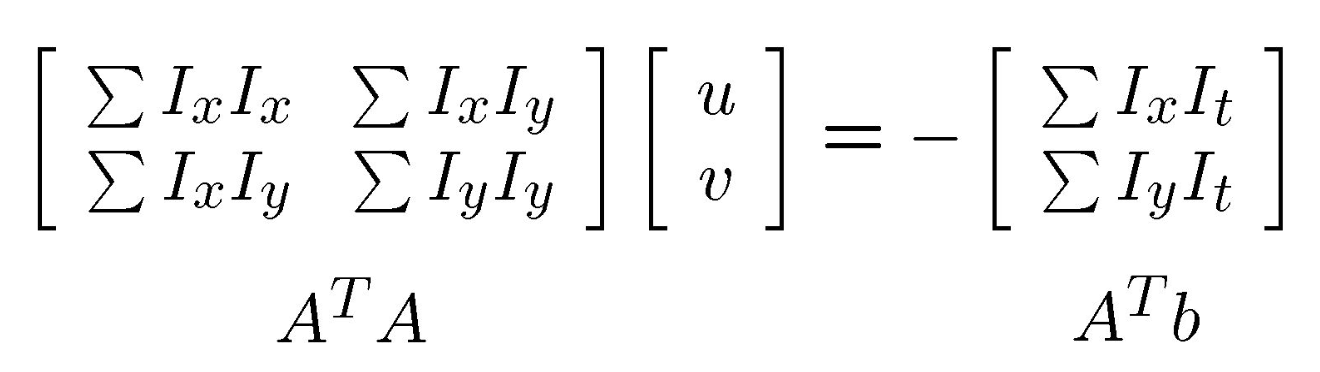
最小二乘法后的式子

上式即是L-K方法求解光流估计问题的方程。通过求解这个方程，就可以得到光流的估计$(u,v)$。但是上式什么时候有解呢？

  • $\mathbf{A}^\dagger \mathbf{A}$是可逆的。
  • $\mathbf{A}^\dagger \mathbf{A}$不应该太小（噪声）。这意味着它的特征值$\lambda_1$, $\lambda_2$不应该太小。
  • $\mathbf{A}^\dagger \mathbf{A}$不应该是病态的（稳定性）。这意味着它的特征值$\lambda_1/\lambda_2$不应该太大。

而我们在Harris角点检测的时候已经讨论过$\mathbf{A}^\dagger \mathbf{A}$这个矩阵的特征值情况了！也许，写成下面的形式更好看出来。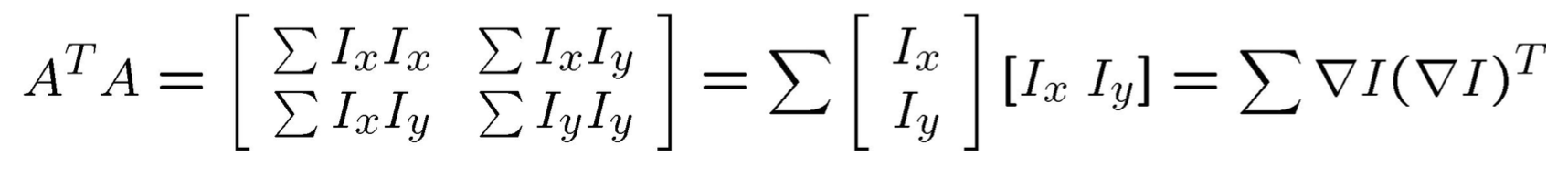
是不是和Harris角点更像了

下面这张图就是当时的讨论结果。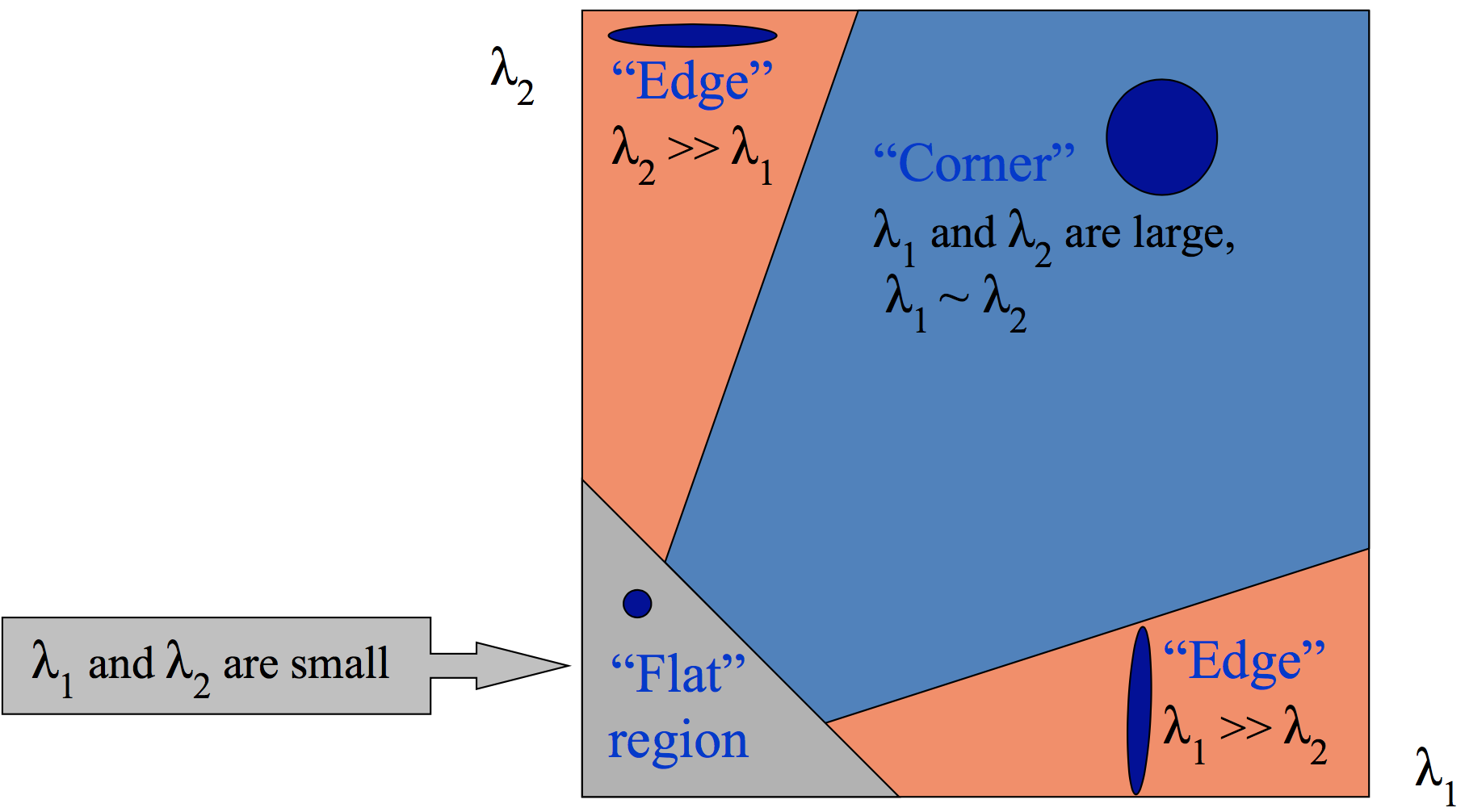
不同点的分类

上面就是使用L-K方法估计光流的一般思路。

金字塔方法

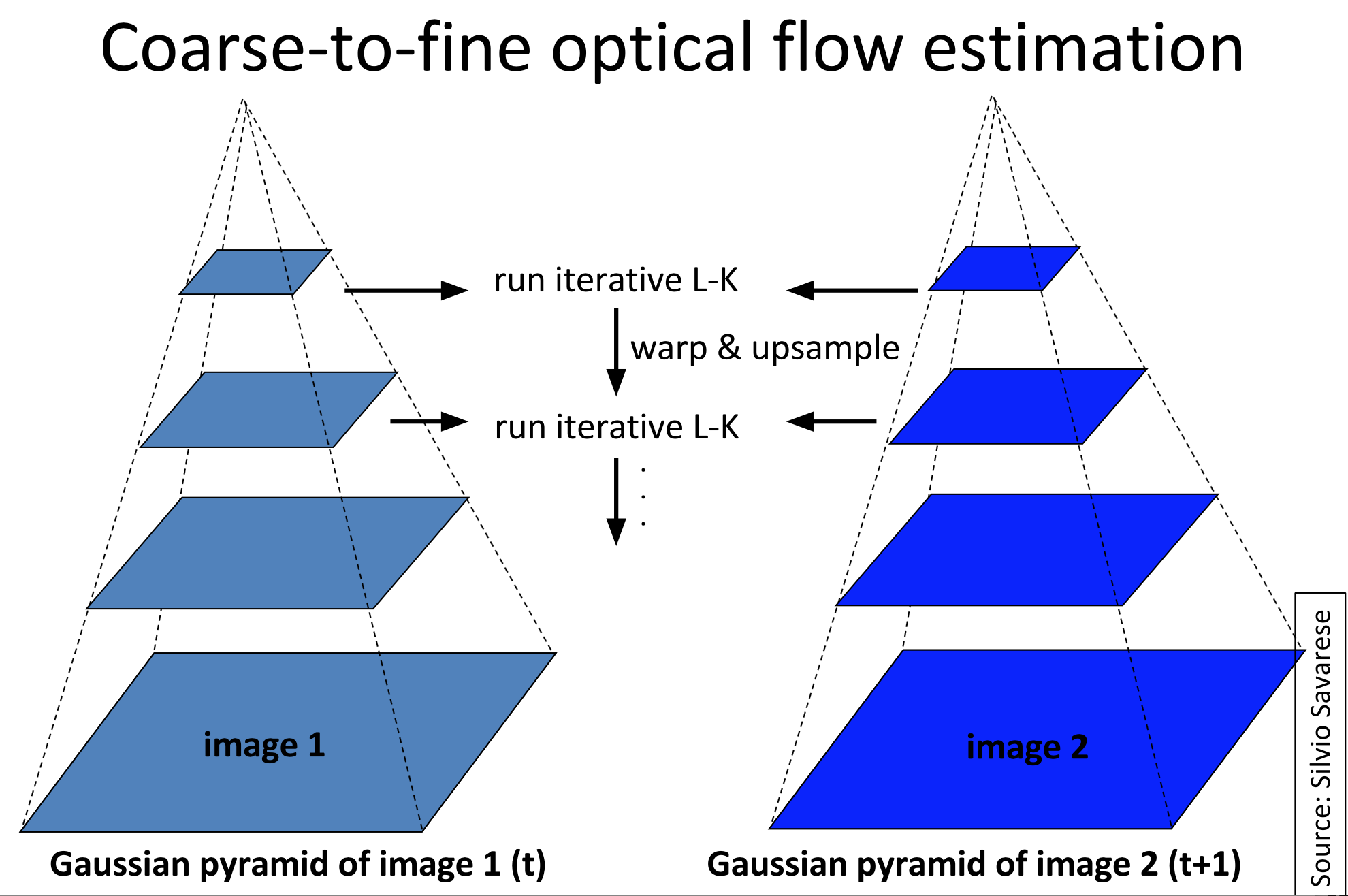
在最开始的假设中，第一条指出点的位移应该是较小的。从上面的分析可以看出，当位移较大时，Taylor展开式一阶近似误差较大。其修正方法就是这里要介绍的金字塔方法。我们通过将图像降采样，就能够使得较大的位移在高层金字塔图像中变小，满足假设条件1.如下所示。

图像金字塔方法

作业：基于光流法的帧间插值

问题描述

假设视频流中的相邻两帧$I_0$和$I_1$，分别标记其时刻为$t=0$和$t=1$。我们希望能够在这两帧之间生成新的插值帧$I_t, 0<t<1$。比如说你手头的视频是24帧的帧率，想在一台刷新频率为60Hz的显示器上播放，那么这项技术可以带来更流畅的观看体验。

简单粗暴法

我们可以简单粗暴地使用线性插值方法，简单的认为插值帧是第一帧和最后一帧的线性组合，也就是说：

这种方法称为”cross-fading”。效果如下。可以看到有较多的模糊抖动。
动图
简单粗暴法效果

基于光流法

使用光流可以知道像素点在图像平面的运动信息，从而在帧间建立点的对应关系。我们记像素点在水平方向和竖直方向的速度分别为$u_t(x,y)$和$v_t(x,y)$。我们可以根据$t=0$和$t=1$的两帧图像解出光流信息，即$u_0(x,y)$和$v_0(x,y)$。那么我们认为光流保持不变，就可以计算插值帧的某一点在$t=0$时候的对应点坐标。接下来，赋值就可以了。如下式所示：

用MATLAB实现如下：

1
2
3
4
5
6
7
for y =1:height
    for x = 1:width
        dy = min(max(round(y+v0(y,x)*t), 1), height);
        dx = min(max(round(x+u0(y,x)*t), 1), width);
        img(dy,dx,:) = img0(y,x,:);
    end
end

这种方法叫做”ForwardWarpping”。效果如下。可以看到，与上一种方法对比，画面有了明显的提升。
动图
逐帧

改进

上面的方法我们假设光流一直保持不变，用$t=1$时刻的光流去代替之间所有时刻的光流。但实际上光流一定是在实时变化的。使用backward warpping改进，使用$t$时刻的光流反推。

然而，我们并不能得到$t$时刻光流$u_t$和$v_t$的准确值，只能近似计算。方法如下：

其中，$x^\prime = x+u_0t$，$y^\prime = y+v_0t$，$\hat{x}\in\lbrace\text{floor}(x^\prime), \text{ceil}(x^\prime)\rbrace$，$\hat{y}\in\lbrace\text{floor}(y^\prime), \text{ceil}(y^\prime)\rbrace$。

这在一定程度上补偿了光流计算的误差。

如果某个点$(\hat{x}, \hat{y})$被多个初始点$(x, y)$对应，那么我们选取使得下面的式子取得最小值的那个点$(x, y)$，也就是选取那个亮度变化最小的点。

如果某个点没有找到相对应的初始点，那么我们使用线性插值方法为其填充光流。

下面是这种方法的效果示意。

动图
逐帧