Hinton 在 Coursera 课程“Neural Network for Machine Learning”新开了一个班次。对课程内容做一总结。课程内容也许已经跟不上最近DL的发展,不过还是有很多的好东西。
Why do we need ML?
从数据中学习,无需手写大量的逻辑代码。ML算法从数据中学习,给出完成任务(如人脸识别)的程序。这里的程序可能有大量的参数组成。得益于硬件的发展和大数据时代的来临,机器学习的应用越来越广泛。如下图所示,MNIST数据集中的手写数字2变化多端,很难人工设计代码逻辑找到判别一个手写数字是不是2的方法。
What are neural network?
为什么要研究神经网络?
- 理解人脑机理的一个途径;
- 受到神经系统启发的并行计算
- 新的学习算法来解决现实问题(本课所关心的)
(这里总结的不是很科学,勉强概括了讲义的内容)
神经元结构如下所示。树突(dendritic tree)和其他神经元相连作为输入,轴突(axon)发散出很多分支和其他神经元相连。轴突和树突之间通过突触(synapse)连接。轴突有足够的电荷产生兴奋。这样完成神经元到神经元的communication。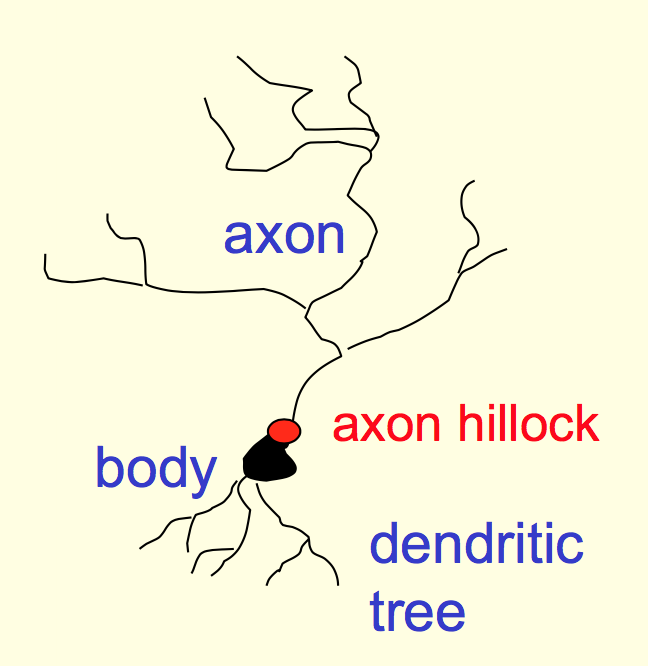
神经元之间互相连接。对不同的神经元输入,有不同的权重。这些权重可以变化,使得神经元之间的连接或变得更加紧密或疏离。人类大脑的神经元多达$10^{11}$个,每一个都有多达$10^4$个连接权重。不同神经元分布式计算,带宽很大。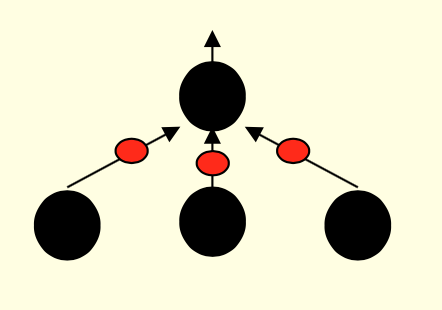
大脑中不同的神经元分工不同(局部损坏造成相应的身体功能受损),但是这些神经元长得都差不多,它们也可以在一定的环境下发育成特定功能的神经元。
而人工神经网络就是根据神经元的兴奋传导机理,人工模拟的神经网络。
Simple models of different neurons
我们简化神经元模型,用数学函数去近似描述它们的功能。这也是科学研究的通用思路,忽略次要矛盾,抓住主要矛盾。之后逐步向上加复杂度,更好地描述实验现象。下面介绍几种神经元的简化模型。
Linear neuron
顾名思义,这种神经元用来进行线性组合的变换,不过要注意加上偏置项。如下所示:
Binary threshold neuron
这种神经元用来将输入信号加权后做二元阈值化,我们可以通过两种方法来描述:
其中,$z$是输入信号的线性组合,$z=\sum_{i}w_ix_i$
或者,
其中,$z$是输入信号的线性组合并加上偏置项,$z = b+\sum_{i}w_ix_i$
Rectified linear neuron
和上面的二值化神经元对比,有:
Sigmoid neuron
这种神经元通过logistic函数将输入shrink到区间$(0, 1)$,如下所示:
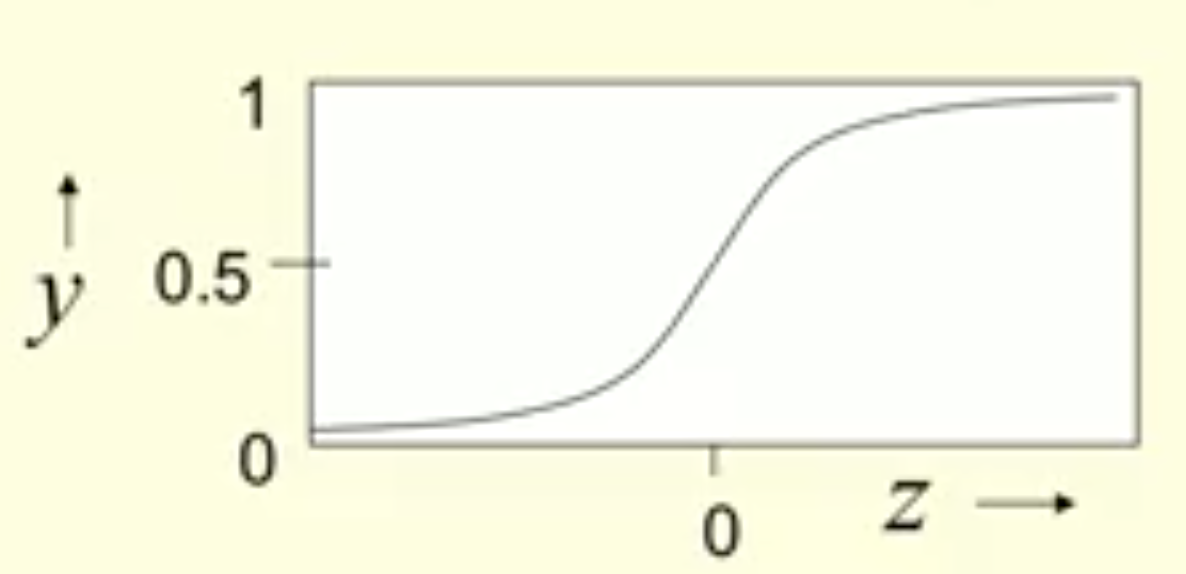
由于Logistic函数将$(-\infty, +\infty)$的值压缩为S型,所以得名Sigmoid。
Stochastic binary neuron
这种函数的输出仍是二值化的,而且是将Logistic函数的输入作为输出$1$的概率。也就是:
对于上面的Rectified linear neuron,也可以做类似的变形,将输出看作是泊松分布的系数。
Three types of learning
即有监督学习,无监督学习和强化学习。
- 有监督学习:给定输入向量,预测输出。
- 无监督学习:学习一个对于输出来说的好的表示(good internal representation of input)。
- 强化学习:学习如何决策达到最大期望奖赏。
有监督学习
有监督学习可以细分为分类和回归问题。有监督学习中,我们需要寻找一个model(由一个函数$f$和决定这个函数的参数$W$决定),将输入$x$应映射为实数(回归问题)或者离散值(分类问题)。
所谓的训练,就是指不断调整参数$W$,使得训练集合中的$x$在当前映射下得到的预测值与真实值之间的差异尽可能小。 在回归问题中,常常使用欧氏距离的平方作为差异的衡量。
强化学习
在强化学习中,算法要给出动作或者动作序列。与有监督学习不同,强化学习中没有真实值,只有不定时(occasional)出现的奖赏。
强化学习的难点如下:
- 奖赏通常是delayed的。以AlphaGo来说,你很难追究中间某一步棋的决策对最后输赢的影响。
- 奖赏通常只是一个标量,提供不了太多的信息。我只能知道这局最后的输赢,但是对于其他信息基本都不知道。
无监督学习
无监督学习以前受到的关注不多,这可能和它的目的不明确有关系。其中一个目的是能够提供输入的更好的表示,以用于强化学习和有监督学习。