这是第二周的课程内容,主要介绍了几种神经网络的分类,详细地介绍了感知机这一最简单的模型。
Different neural network archs
Feed-forward neural network 前馈神经网络
前馈神经网络可能是最常见的网络,主要由输入层,若干隐含层和输出层组成。一般,当隐含层数目超过$1$时,我们可以说网络是deep的。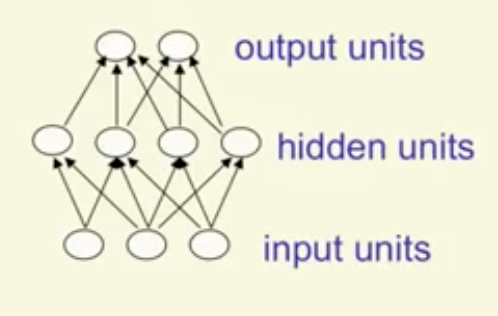
Recurrent network
RNN内部的节点之间存在有向的环,这使得它能够使用内部状态来对动态过程建模。RNN能力强大,但是不易训练。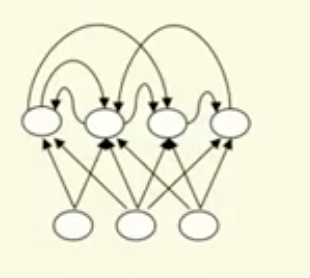
RNN常用来对序列进行建模(modeling squence)。这里有一篇不错的介绍。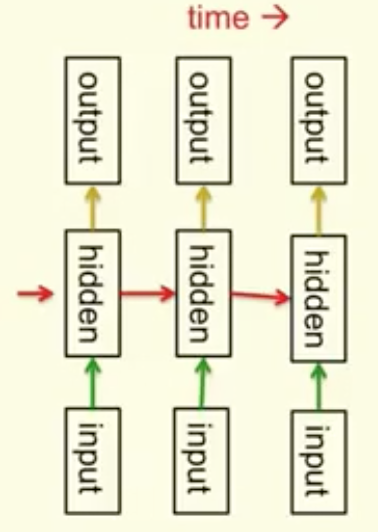
Symmetrically connected network
这种网络结构上很像RNN,但是它的节点之间的连接是对称的,意思是说由此到彼和由彼到此的权重相同。
Percetron
训练
最早的神经网络应用是感知机。使用感知机等统计学习方法进行模式分类的一般思路是:
- 将原始输入向量转化为feature activation。
- 寻找合适的权重对feature进行加权,得到某个标量。
- 如果这个标量大于某一给定的阈值,则分类为正;否则分类为负。
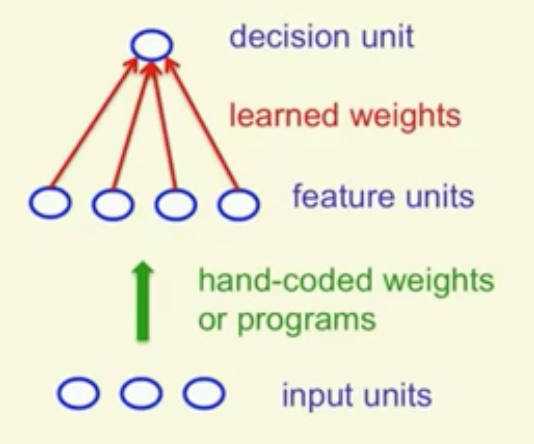
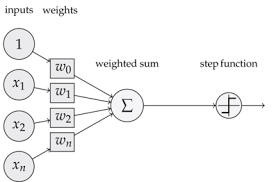
对于决策节点,常常使用Binary threshold neuron,将输入映射为${0,1}$。而这相当于给输入加上一个偏置项,然后和$0$比较。
所以,感知机的数学模型可以描述如下:
训练时,遍历样本集中的样本点,根据真实值与预测值是否相同,有如下的更新方法:
- 若预测值与真实值相同,则不作调整;
- 否则,若错输出为$0$,则将输入的$x$加到权重$w$上去;
- 若错输出为1,则从权重$w$上将输入的$x$减去。
当训练集确实是线性可分的时候,这种方法能够保证找到那样的一组参数,使得样本集完全正确分类。
原理
下面从几何角度分析一下感知机。
权重空间(Weight Space的概念),对于权重向量的每个分量,都有一个维度对应。空间中的某个点就代表一个权重的实例。
让我们忽略偏置项,那么每个训练样本都可以看作是权重空间的分类超平面。这个超平面的方程可以写作$x^\dagger w = 0$,平面的法向量就是输入样本$x$。下图中假设输入样本为正样本,黑线即为超平面。平面上方的权重都是正确的(例如绿色的那个),下方的则都会使得该样本分类错误(红色的那个)。因为黑线上方的那些权重和输入$x$的夹角小于直角,也就是说内积是大于$0$的,自然就会给出正样本的预测。反之同理。
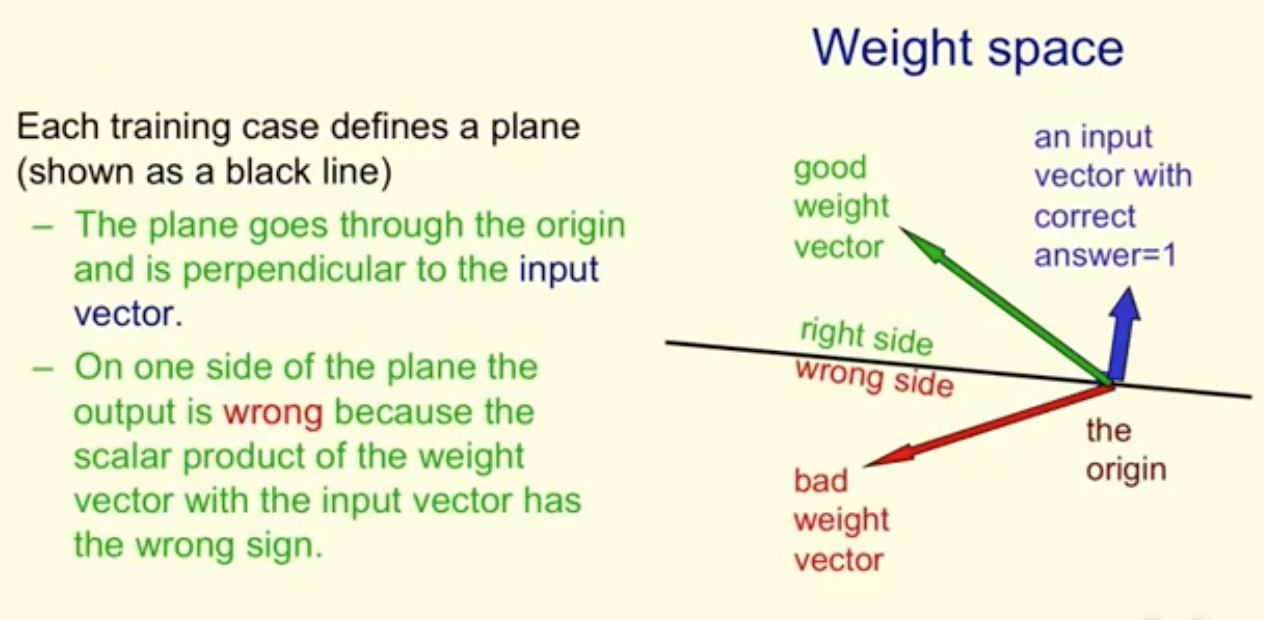
当输入样本为负样本时,分析同理。只不过正确的权重此时应该位于平面下方,与输入向量夹角大于直角。
所以,感知机的参数调整就是要在权重空间内找到某个权重点,使其在所有的训练样本构成的这么多超平面都位于正确的位置。
下面用刚才的这种思考方式证明上述训练方法的正确性。
首先考虑当前的权重和最终要找的那个权重之间的距离平方为$d_a^2+d_b^2$,如图所示。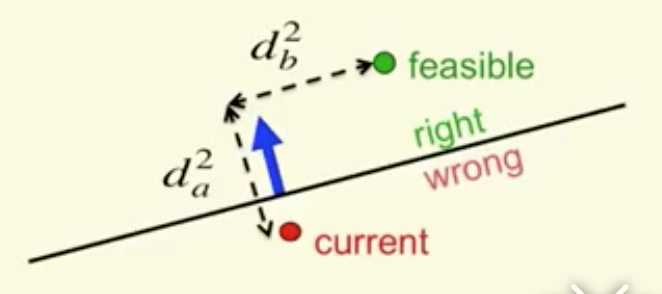
我们希望,对于每个错分的样例,学习算法能够将当前的参数向正确的参数推进。对照上图,似乎我们只要加上蓝色的那个输入向量就可以了。然而如果输入向量长度较长,而我们离正确的权值又比较近了,有可能出现更加远离的情况。
我们取一个margin,认为我们要找的那个权重可行域不仅要满足分类正确,还要保证分类面和可行域的距离大于margin。(这里不是很懂,这样来看可行域的条件更加苛刻了,如果有正确分类面却没有这样的可行域呢?有可能出现吗?感知机这里还是看李航的统计学习更清楚点。。。我还是喜欢解析而不是几何。。。)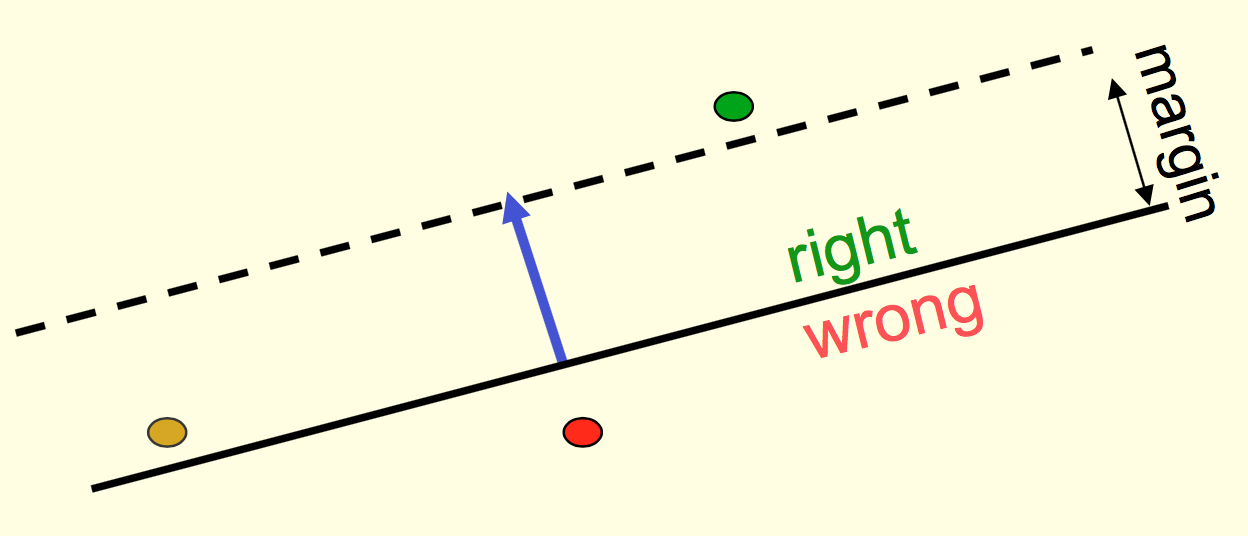
每次做出一次错误分类,权重根据输入向量做更新,向可行域前进至少input vector的长度这么多。这样不停迭代,就能收敛。(前面还提到了这是一个凸优化,也是一脸懵逼。。。)
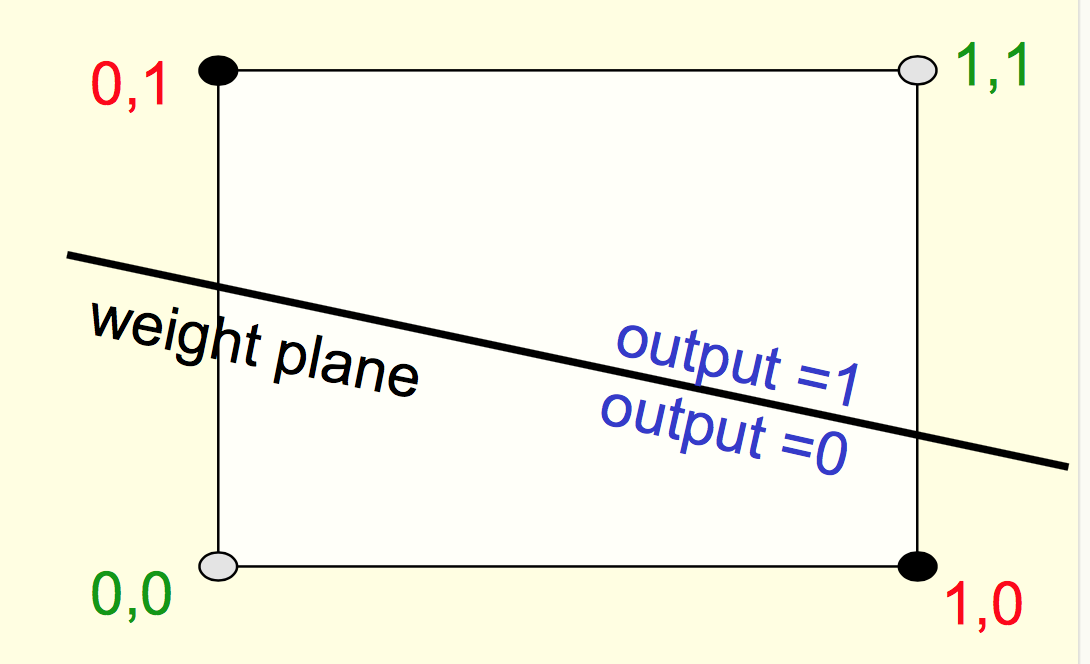
感知机的局限
感知机不能解决线性不可问题,如异或运算。通过做特征变换,选取不同的特征,可能可以解决。