来呀，快活呀~

Silver RL课程 - DP Planning

发表于

上讲中介绍了MDP这一基本概念。之后的lecture以此出发，介绍不同情况下的最优策略求解方法。本节假设我们对MDP过程的所有参数都是已知的，这时候问题较为简单，可以直接得到确定的解。这种问题叫做planning问题，求解方法是动态规划。

动态规划

动态规划是计算机科学中常用的思想方法。对于一个复杂的问题，我们可以将它划分成若干的子问题，然后再将子问题的解答合并为原问题的解。要想用动态规划解决问题，该问题必须满足以下两个条件：

  • 最优子结构。能够分解为若干子问题。
  • 子问题重叠。分解后的子问题存在重叠，我们可以通过记忆化的方法进行缓存和重用。

MDP问题的求解符合上述要求。贝尔曼方程给出了原问题递归的分解（考虑状态$S$时，我们可以考虑从状态$s$出发的下一个状态$s^\prime$，而在考虑状态$s^\prime$的时候，问题和原问题是一样的，只不过问题规模变小了）；而使用值函数我们相当于记录了中间结果。值函数充当了缓存与记事簿的作用。

迭代策略估计

给定一个策略，我们想要知道该策略的期望回报是多少，也就是其对应的值函数$v_\pi(s)$。首先回顾一下上讲中得到的值函数的贝尔曼方程如下（全概率公式）：

我们有如下的迭代估计方法：在每一轮迭代中，对于所有状态$s\in \mathcal{S}$，使用上式利用上轮中的$v(s^\prime)$更新$v_{k+1}(s)$，直到收敛。

给出下面的算例。$4\times 4$的格子中，$0$和$15$是出口。在状态$0$和$15$向自身转移时，奖赏为$0$。其他状态来回转换时，奖赏均为$-1$。如果当前移动使得更新后的位置超过格子的边界，则状态仍然保持原状。求采取随机策略$\pi$，即每个状态下，上下左右四个方向移动的概率均为$0.25$时候各个状态的值函数$v_\pi(s)$。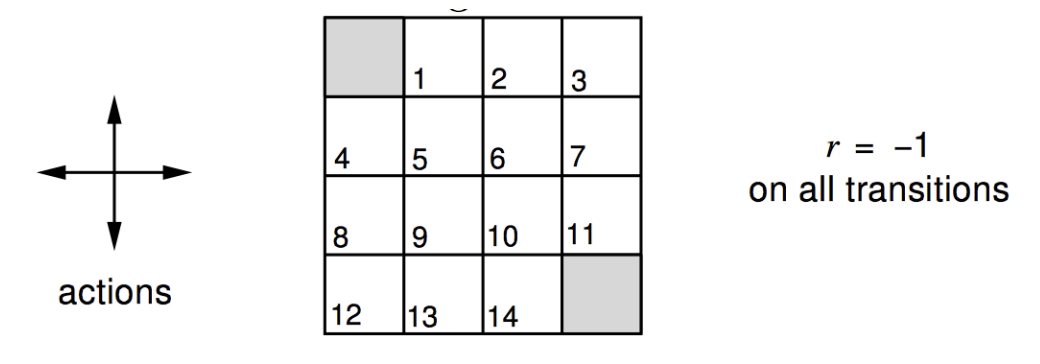
Demo

这里直接将Python实现的计算过程贴在下面，注意在每一轮迭代开始前，暂存当前值函数的副本。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
import numpy as np

v = [0 for _ in xrange(16)]
line1 = range(1, 4)
line4 = range(12, 15)
col1 = [4, 8, 12]
col4 = [3, 7, 11]


# the environment simulator
def get_new_loc(idx, action):
    if idx == 0 or idx == 15:
        ret = idx
        reward = 0
        return ret, reward

    if action == 0:
        # up
        if idx in line1:
            ret = idx
        else:
            ret = idx-4
    elif action == 1:
        # down
        if idx in line4:
            ret = idx
        else:
            ret = idx+4
    elif action == 2:
        # left
        if idx in col1:
            ret = idx
        else:
            ret = idx-1
    elif action == 3:
        # right
        if idx in col4:
            ret = idx
        else:
            ret = idx+1

    reward = -1
    return ret, reward


gamma = 1.

K = [1, 2, 3, 10, 100]
for k in xrange(1, 101):
    # in each iteration, update v(s) via:
    # v(s) = \sum_a \pi(a|s) + \gamma \sum_s^\prime P_{ss^\prime}^a v(s^\prime)
    v_aux = v[:]
    for i in xrange(16):
        v_aux[i] = 0.
        for action in range(4):
            j, r = get_new_loc(i, action)
            v_aux[i] += 0.25*(r+gamma*v[j])
    v = v_aux
    if k in K:
        print 'k = {} '.format(k),
        print ', '.join(map(lambda x: '{:.1f}'.format(x), v))

策略的改进

评估过某个策略的值函数后，我们可以改进该策略，使用的方法为贪心法。具体来说，在某个状态$s$时，我们更新此时的动作为能够使得$Q(s,a)$取得最大，接下来继续执行原策略的那个动作（也就是我们只看一步）。如下所示：

以上小节中给出的算例为例，最终值函数结果为：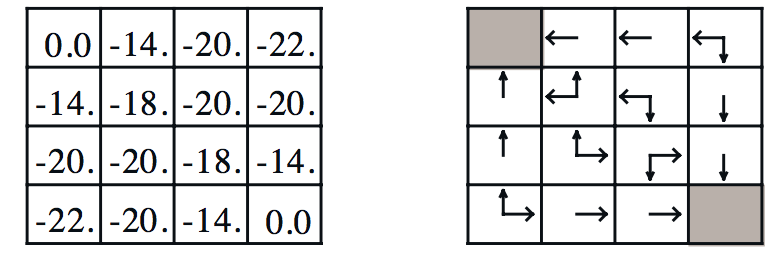
策略估计结果

那么对于位置$1$，由于其左方的状态值函数最大，为$0$。所以，我们认为从位置$1$出发的最优策略应该是向左移动。其他同理。这样，对于任何一个状态，它都可以通过选取$q(s,a)$最大的那个动作达到下一个状态，再递推地走下去（如右侧图中的箭头所示）。

为什么这种贪心方法有效呢？这里直接把证明过程粘贴如下。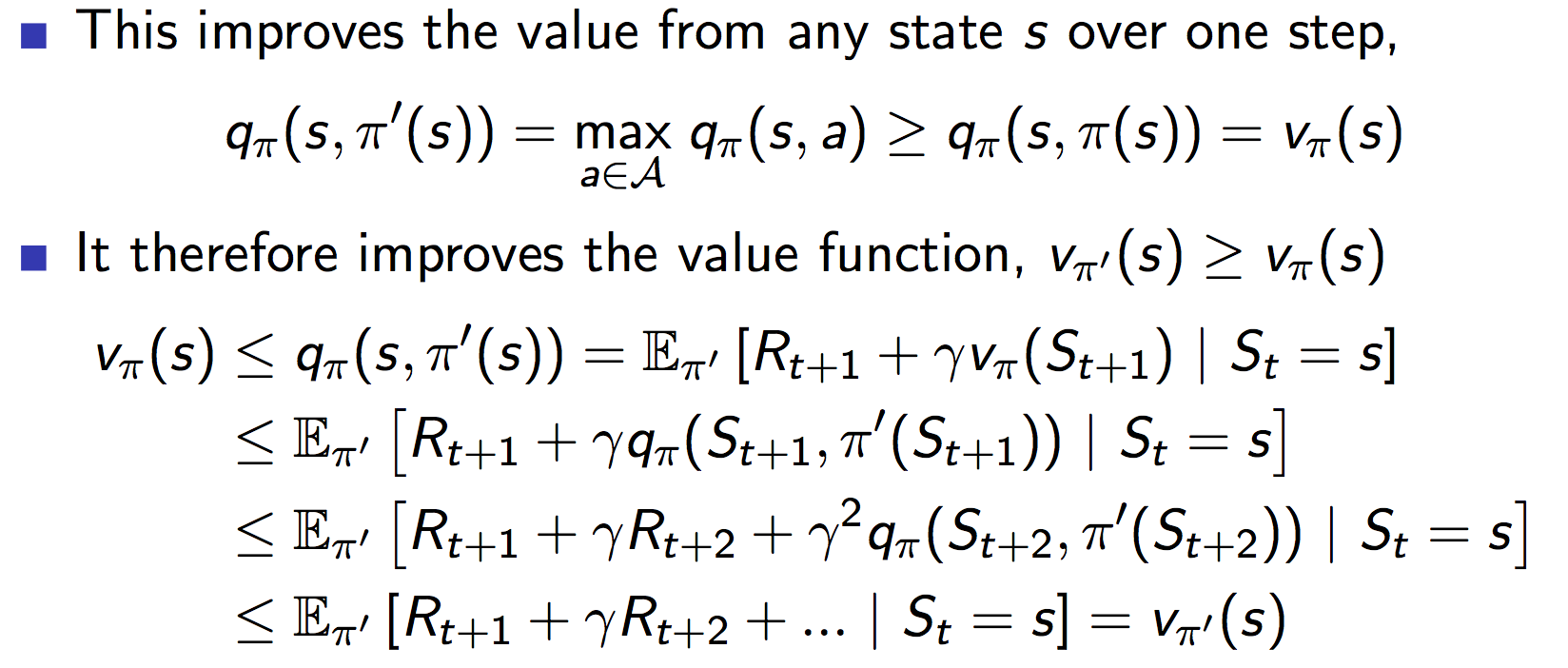
贪心方法work的证明

当上述单步提升不再满足时，上图中的不等号就变成了等号，算法收敛到了最优解。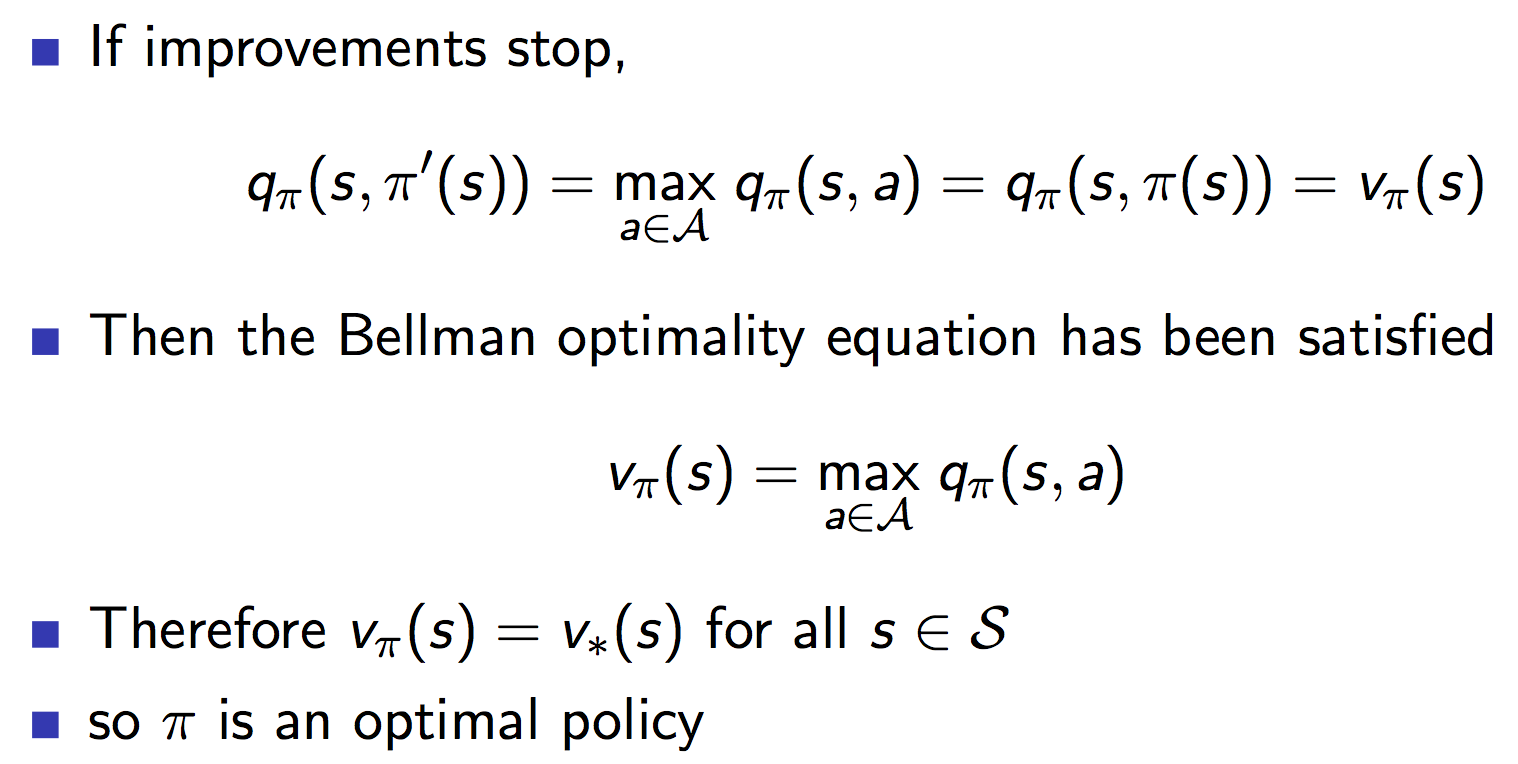
贪心方法的终止

值迭代

首先介绍最优化定理（也可以解释上述贪心方法为什么work，类比图中最短路径的分析）。这条定理是说某个策略对于状态$s$是最优的，当且仅当，对于每个由$s$出发可达的状态$s^\prime$，都有，该策略对$s^\prime$也是最优的。这提示我们，可以通过下面的式子更新$s$处的最优值函数的值。

通过迭代地进行这个步骤，就能够收敛到最优值函数。每次迭代中，都首先计算最后一个状态的值函数，然后逐渐回滚，更新前面的。如下图所示（求取最短路径）：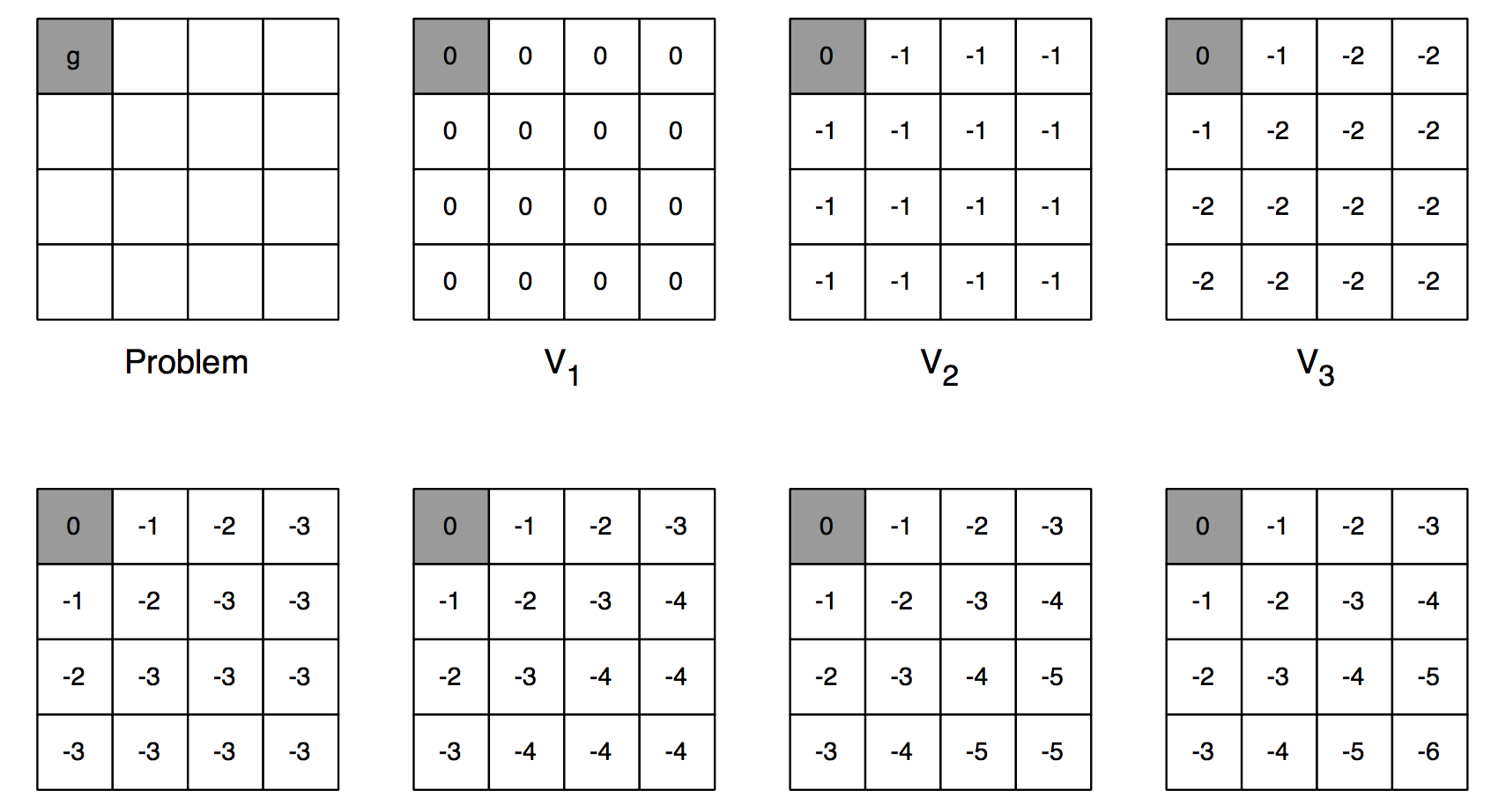
值迭代方法示例

每轮迭代，都从$1$号开始。考虑$1$号，第一轮时候，大家都是$0$。当选取动作为向左移动时候，上式取得最大值。所以$s^\prime=0$。更新之后，其值变为了$-1$（因为把reward加上去了），接下来更新其他。并开始新的迭代轮次，最终收敛。

注意到，这里和上面策略迭代-改进来求取最优策略不同，这里并不存在一个显式的策略。或者说，在策略迭代的时候，我们是要选取某个动作$a$，使得值-动作函数$q(s,a)$取值最大。而在值迭代的过程中，我们只关心下个状态的值函数和在这个转换过程中得到的奖励。

异步DP

上面我们讨论的是同步迭代更新。也就是说，在更新前，我们要先备份各个状态的值函数，更新时是使用状态$s^\prime$的旧值来计算$s$的新值。如下图所示：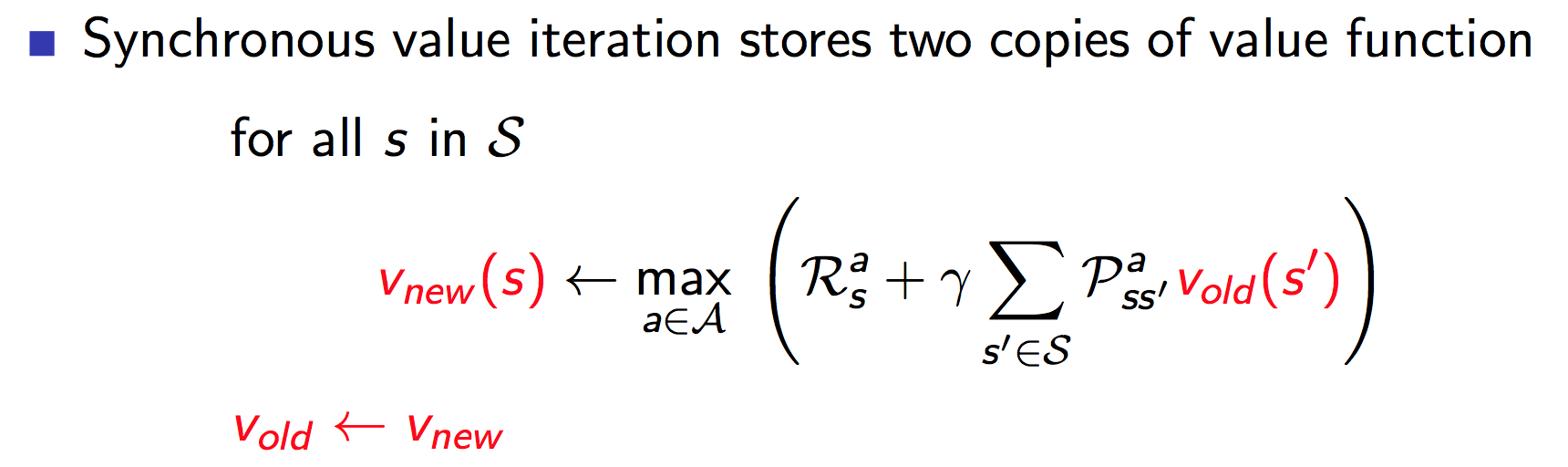
同步更新
上面讨论了同步迭代的三个主要问题：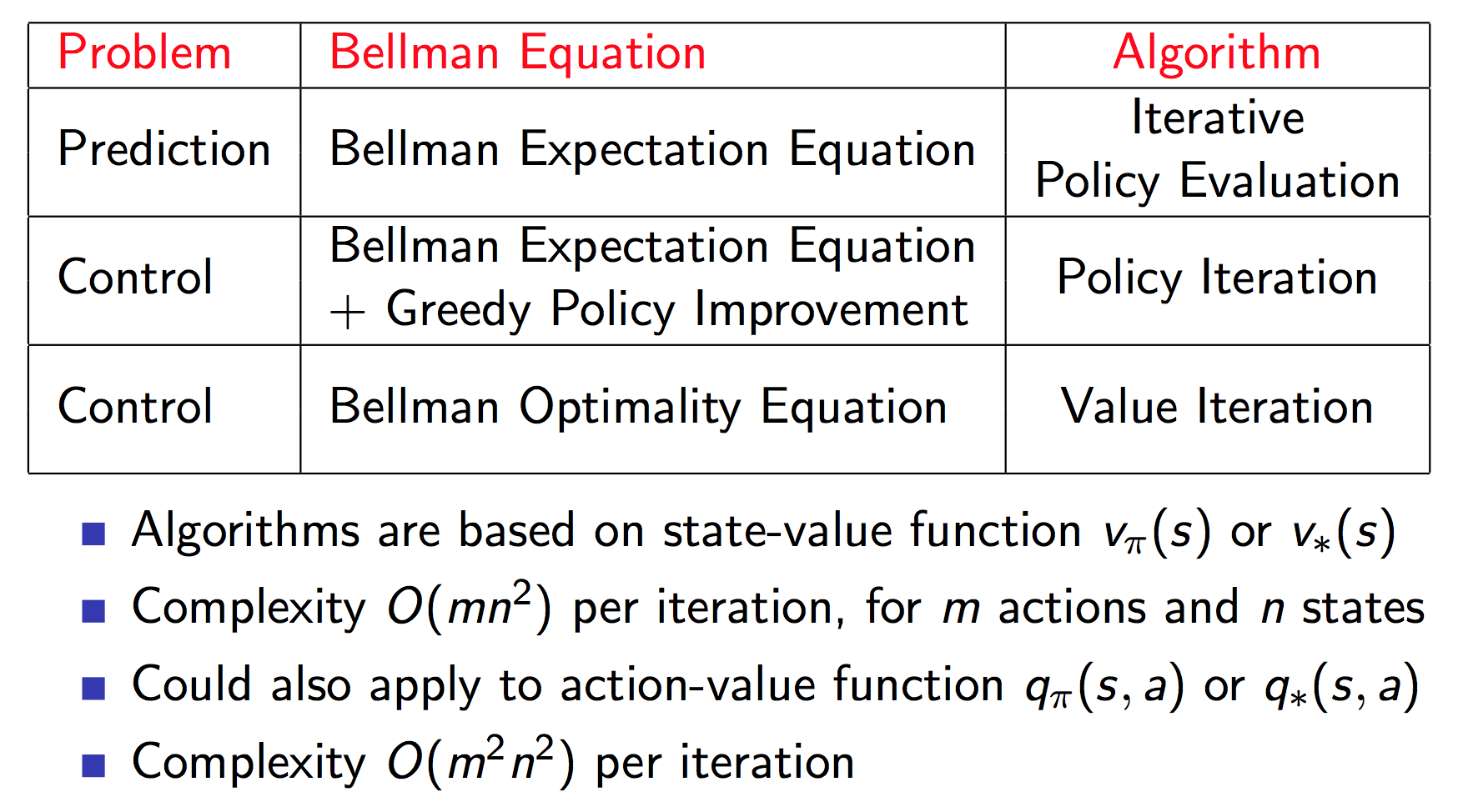
同步更新问题

我们也可以使用异步方法。主要包括以下三种：

就地（in-place） DP

就地DP只存储一份值函数，在更新时，有可能在使用新的状态值函数$v_{\text{new}}(s^\orime)$来更新$v(s)$。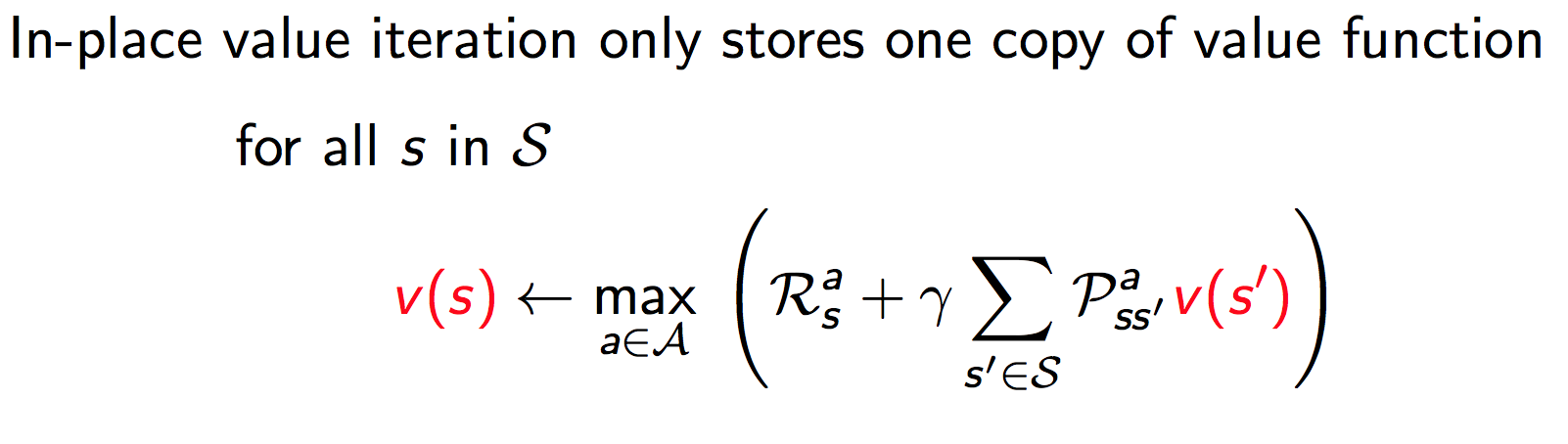
就地更新迭代值函数

带有优先级的状态扫描（Prioritized Sweeping）

根据贝尔曼方程的误差来指示更新先更新哪个状态的值函数，即

实现的具体细节如下：

实时DP

使用智能体与环境交互的经验（experience）来挑选状态。
实时DP