Neural Network for Machine Learning - Lecture 06 神经网络的“调教”方法

第六周的课程主要讲解了用于神经网络训练的梯度下降方法，首先对比了SGD，full batch GD和mini batch SGD方法，然后给出了几个用于神经网络训练的trick，主要包括输入数据预处理（零均值，单位方差以及PCA解耦），学习率的自适应调节以及网络权重的初始化方法（可以参考各大框架中实现的Xavier初始化方法等）。这篇文章主要记录了后续讲解的几种GD变种方法，如何合理利用梯度信息达到更好的训练效果。由于Hinton这门课确实时间已经很久了，所以文章末尾会结合一篇不错的总结性质的博客和对应的论文以及PyTorch中的相关代码，对目前流行的梯度下降方法做个总结。

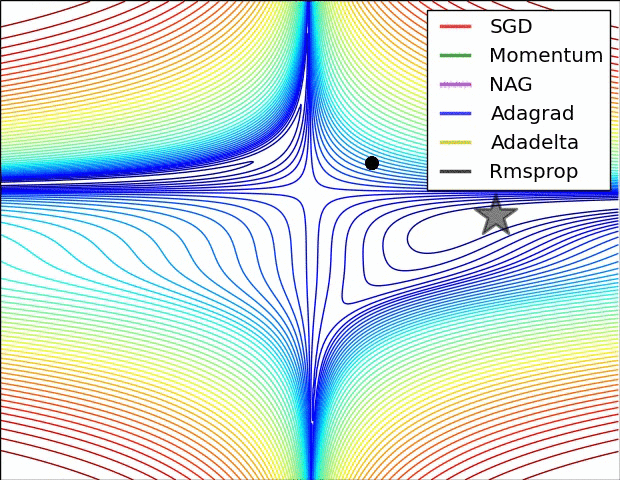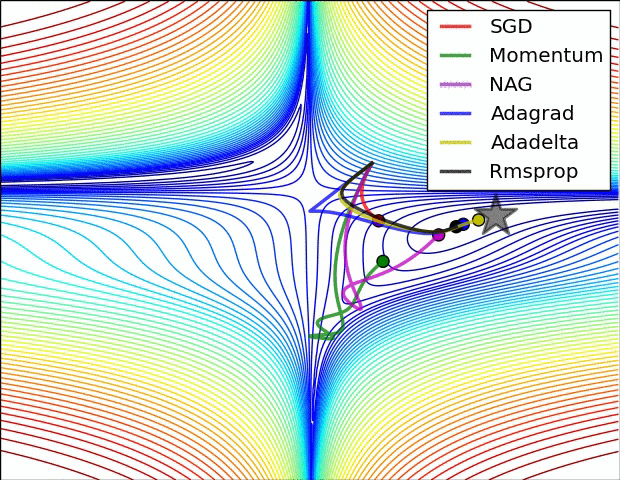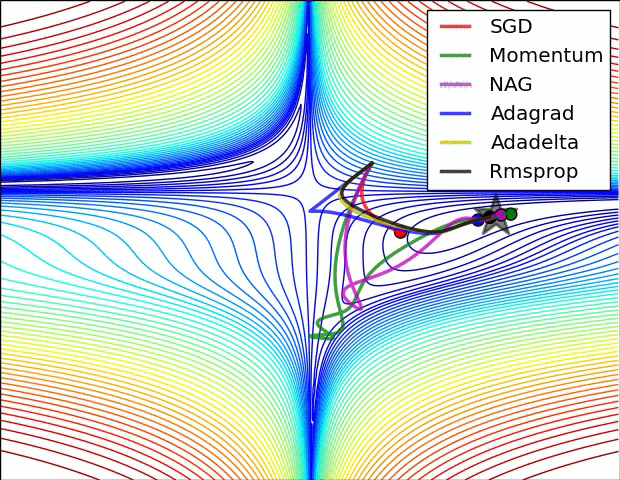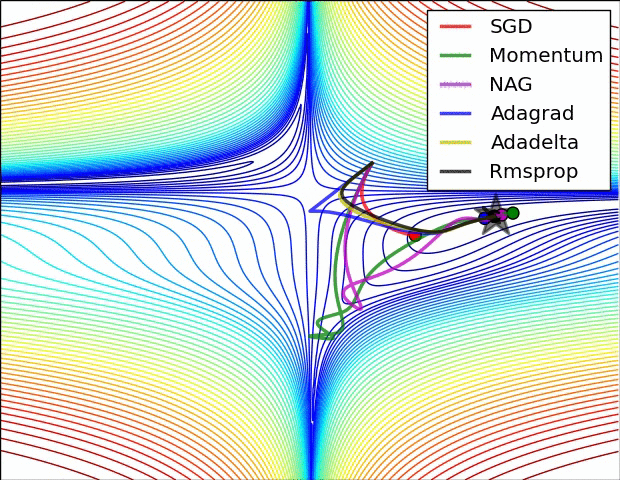
下图即来自上面的这篇博客。

Momentum

我们可以把训练过程想象成在权重空间的一个质点（小球），移动到全局最优点的过程。不同于GD，使用梯度信息直接更新权重的位置，momentum方法是将梯度作为速度量。这样做的好处是，当梯度的方向一直不变时，速度可以加快；当梯度方向变化剧烈时，由于符号改变，所以速度减慢，起到了GD中自适应调节学习率的过程。

具体来说，我们利用新得到的梯度信息，采用滑动平均的方法更新速度。式子中的$\epsilon$为学习率，$\alpha$为momentum系数。

$$\Delta w_t = v_t = \alpha v_{t-1} - \epsilon g_t = \Delta w_t - \epsilon g_t$$

为了说明momentum确实对学习过程有加速作用，假设一个简单的情形，即运动轨迹是一个斜率固定的斜面。那么我们有梯度$g$固定。根据上面的递推公式可以得到通项公式（简单的待定系数法凑出等比数列）：

$$v_t = \alpha(v_{t-1} + \frac{\epsilon g}{1-\alpha}) - \frac{\epsilon g}{1-\alpha}$$

由于$\alpha < 0$，所以当$t = \infty$时，只剩下了后面的常数项，即：

$$v_\infty = -\frac{\epsilon}{1-\alpha}g$$

也就是说，权重更新的幅度变成了原来的$\frac{1}{1-\alpha}$倍。若取$\alpha=0.99$，则加速$100$倍。

Hinton给出的建议是由于训练开头梯度值比较大，所以momentum系数一开始不要过大，例如可以取$0.5$。当梯度值较小，训练过程被困在一个峡谷的时候，可以适当提升。

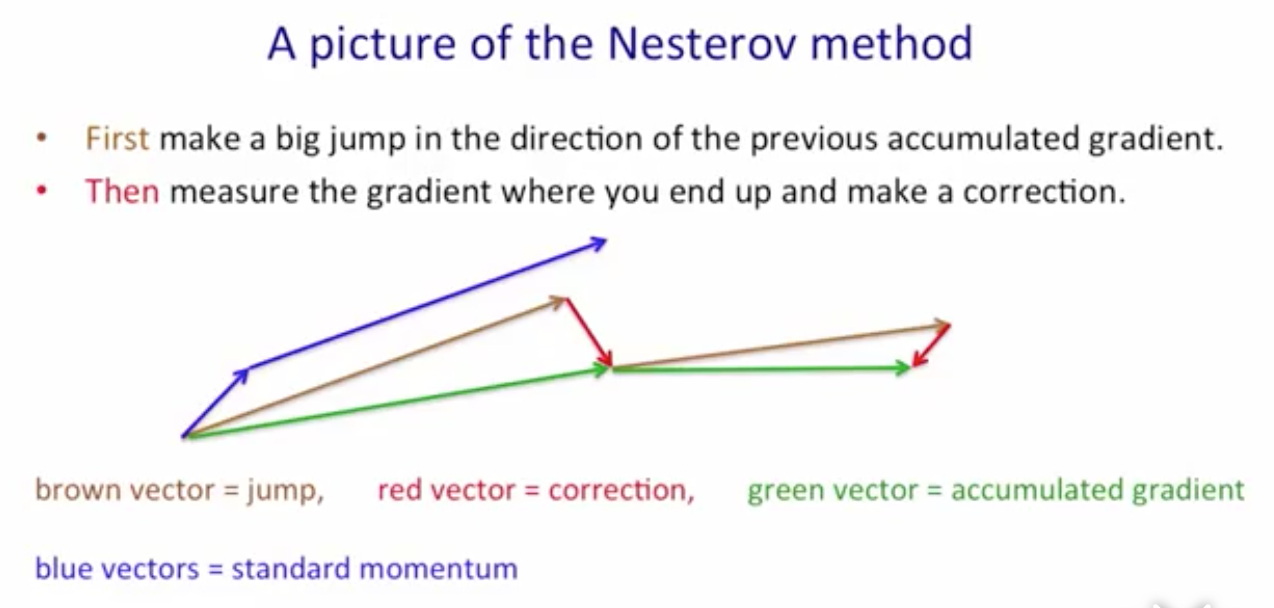
一种改进方法由Nesterov提出。在上面的方法中，我们首先更新了在该处的累积梯度信息，然后向前移动。而Nesterov方法中，我们首先沿着累计梯度信息向前走，然后根据梯度信息进行更正。

Adaptive Learning Rate

这种方法起源于这样的观察：在网络中，不同layer之间的权重更新需要不同的学习率。因为浅层和深层的layer梯度幅值很可能不同。所以，对不同的权重乘上不同的因子是个更加合理的选择。

例如，我们可以根据梯度是否发生符号变化按照下面的方式调节某个权重$w_{ij}$的增益。注意$0.95$和$0.05$的和是$1$。这样可以使得平衡点在$1$附近。

下面是使用这种方法的几个trick，包括限幅，较大的batch size以及和momentum的结合。

RMSProp

rprop利用梯度的符号，如果符号保持不变，则相应增大step size；否则减小。但是只能用于full batch GD。RMSProp就是一种可以结合mini batch SGD和rprop的一种方法。

我们使用滑动平均方法更新梯度的mean square（即RMS中的MS得来）。

$$\text{MeanSquare}(w, t) = 0.9 \text{MeanSquare}(w, t-1) + 0.1g_t^2$$

然后，将梯度除以上面的得到的Mean Square值。

RMSProp还有一些变种，列举如下：

课程总结

• 对于小数据集，使用full batch GD（LBFGS或adaptive learning rate如rprop）。
• 对于较大数据集，使用mini batch SGD。并可以考虑加上momentmum和RMSProp。

如何选择学习率是一个较为依赖经验的任务（网络结构不同，任务不同）。

“Modern” SGD

从本部分开始，我将转向总结摘要中提到的那篇博客中的主要内容。首先，给出当前基于梯度的优化方法的一些问题。可以看到，之后人们提出的改进方法就是想办法解决对应问题的。由于与Hinton课程相比，这些方法提出时间（也许称之为流行时间更合适？做数学的那帮人可能很早就知道这些优化方法了吧？）较短，所以这里仿照Modern C++之称呼，就把它们统一叫做Modern SGD吧。。。

• 学习率通常很难确定。学习率太大？容易扯到蛋（loss直接爆炸）；学习率太小，训练到天荒地老。。。
• 学习率如何在训练中调整。目前常用的方法是退火，要么是固定若干次迭代之后把学习率调小，要么是观察loss到某个阈值后把学习率调小。总之，都是在训练开始前，人工预先定义好的。而这没有考虑到数据集自身的特点。
• 学习率对每个网络参数都一样。这点在上面课程中Hinton已经提到，引出了自适应学习率的方法。
• 高度非凸函数的优化难题。以前人们多是认为网络很容易收敛到局部极小值。后来有人提出，网络之所以难训练，更多是由于遇到了鞍点。也就是某个方向上它是极小值；而另一个方向却是极大值（高数中介绍过的，马鞍面）

Adagrad

Adagrad对不同的参数采用不同的学习率，也是其Ada（Adaptive）的名字得来。我们记时间步$t$时标号为$i$的参数对应的梯度为$g_{i}$，即：

$$g_{i} = \bigtriangledown_{\theta_i} J(\theta)$$

Adagrad使用一个系数来为不同的参数修正学习率，如下：

$$\hat{g_i} = \frac{1}{\sqrt{G_i+\epsilon}}g_i$$

其中，$G_i$是截止到当前时间步$t$时，参数$\theta_i$对应梯度$g_i$的平方和。

我们可以把上面的式子写成矩阵形式。其中，$\odot$表示逐元素的矩阵相乘（element-wise product）。同时，$G_t = g_t \odot g_t$。

$$\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{G_t+\epsilon}}\odot g_t$$

我们再来看PyTorch中的相关实现：

# for each gradient of parameters:
# addcmul(t, alpha, t1, t2): t = t1*t2*alpha + t
# let epsilon = 1E-10
state['sum'].addcmul_(1, grad, grad)   # 计算 G
std = state['sum'].sqrt().add_(1e-10)  # 计算 \sqrt(G)
p.data.addcdiv_(-clr, grad, std)       # 更新

由于Adagrad对不同的梯度给了不同的学习率修正值，所以使用这种方法时，我们可以不用操心学习率，只是给定一个初始值（如$0.01$）就够了。尤其是对稀疏的数据，Adagrad方法能够自适应调节其梯度更新信息，给那些不常出现（非零）的梯度对应更大的学习率。PyTorch中还为稀疏数据特别优化了更新算法。

Adagrad的缺点在于由于$G_t$矩阵是平方和，所以分母会越来越大，造成训练后期学习率会变得很小。下面的Adadelta方法针对这个问题进行了改进。

Adadelta

Adadelta给出的改进方法是不再记录所有的历史时刻的$g$的平方和，而是最近一个有限的观察窗口$w$的累积梯度平方和。在实际使用时，这种方法使用了一个参数$\gamma$（如$0.9$）作为遗忘因子，对$E[g_t^2]$进行统计。

$$E[g_t^2] = \gamma E[g_{t-1}^2] + (1-\gamma)g_t^2$$

由于$\sqrt{E[g_t^2]}$就是$g$的均方根RMS，所以，修正后的梯度如下。注意到，这正是Hinton在课上所讲到的RMSprop的优化方法。

$$\hat{g}_t = \frac{1}{\text{RMS}[g]}g_t$$

作者还观察到，这样更新的话，其实$\theta$和$\Delta \theta$的单位是不一样的（此时$\Delta \theta$是无量纲数）。所以，作者提出再乘上一个$\text{RMS}[\Delta \theta]$来平衡（同时去掉了学习率$\eta$），所以，最终的参数更新如下：

$$\theta_{t+1} = \theta_t - \frac{\text{RMS}[\Delta \theta]}{\text{RMS}[g]}g_t$$

这种方法甚至不再需要学习率。下面是PyTorch中的实现，其中仍然保有学习率lr这一参数设定，默认值为$1.0$。代码注释中，我使用MS来指代$E[x^2]$。即，$\text{RMS}[x] = \sqrt{\text{MS}[x]+\epsilon}$。

# update: MS[g] = MS[g]*\rho + g*g*(1-\rho)
square_avg.mul_(rho).addcmul_(1 - rho, grad, grad)
# current RMS[g] = sqrt(MS[g] + \epsilon)
std = square_avg.add(eps).sqrt_()
# \Delta \theta = RMS[\Delta \theta] / RMS[g]) * g
delta = acc_delta.add(eps).sqrt_().div_(std).mul_(grad)
# update parameter: \theta -= lr * \Delta \theta
p.data.add_(-group['lr'], delta)
# update MS[\Delta \theta] = MS[\Delta \theta] * \rho + \Delta \theta^2 * (1-\rho)
acc_delta.mul_(rho).addcmul_(1 - rho, delta, delta)

Adam

Adaptive momen Estimation（Adam，自适应矩估计），是另一种为不同参数自适应设置不同学习率的方法。Adam方法不止存储过往的梯度平方均值（二阶矩）信息，还存储过往的梯度均值信息（一阶矩）。

$$\begin{aligned}m_t&=\beta_1 m_{t-1}+(1-\beta_1)g_t\\v_t&=\beta_2 v_{t-1}+(1-\beta_2)g_t^2\end{aligned}$$

作者观察到上述估计是有偏的（biase towards $0$），所以给出如下修正：

$$\begin{aligned}\hat{m} &= \frac{m}{1-\beta_1}\\ \hat{v}&=\frac{v}{1-\beta_2}\end{aligned}$$

参数的更新如下：

$$\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v_t} + \epsilon}}\hat{m_t}$$

作者给出$\beta_1 = 0.9$，$\beta_2=0.999$，$\epsilon=10^{-8}$。

为了更好地理解PyTorch中的实现方式，需要对上式进行变形：

$$\Delta \theta = \frac{\sqrt{1-\beta_2}}{1-\beta_1}\eta \frac{m_t}{\sqrt{v_t}}$$

代码中令$\text{step_size} = \frac{\sqrt{1-\beta_2}}{1-\beta_1}\eta$。同时，$\beta$也要以指数规律衰减，即：$\beta_t = \beta_0^t$。

# exp_avg is `m`: expected average of g
exp_avg.mul_(beta1).add_(1 - beta1, grad)
# exp_avg_sq is `v`: expected average of g's square
exp_avg_sq.mul_(beta2).addcmul_(1 - beta2, grad, grad)

# \sqrt{v_t + \epsilon}
denom = exp_avg_sq.sqrt().add_(group['eps'])

# 1 - \beta_1^t
bias_correction1 = 1 - beta1 ** state['step']
# 1 - \beta_2^t
bias_correction2 = 1 - beta2 ** state['step']
# get step_size
step_size = group['lr'] * math.sqrt(bias_correction2) / bias_correction1
# delta = -step_size * m / sqrt(v)
p.data.addcdiv_(-step_size, exp_avg, denom)

AdaMax

上面Adam中，实际上我们是用梯度$g$的$2$范数（$\sqrt{\hat{v_t}}$）去对$g$进行Normalization。那么为什么不用其他形式的范数$p$来试试呢？然而，对于$1$范数和$2$范数，数值是稳定的。对于再大的$p$，数值不稳定。不过，当取无穷范数的时候，又是稳定的了。

由于无穷范数就是求绝对值最大的分量，所以这种方法叫做AdaMax。其对应的$\hat{v_t}$为（这里为了避免混淆，使用$u_t$指代）：

$$u_t = \beta_2^\infty u_{t-1} + (1-\beta_2^\infty) g_t^\infty$$

我们将$u_t$按照时间展开，可以得到（直接摘自论文的图）。其中最后一步递推式的得来：根据$u_t$把$u_{t-1}$的展开形式也写出来，就不难发现最下面的递推形式。

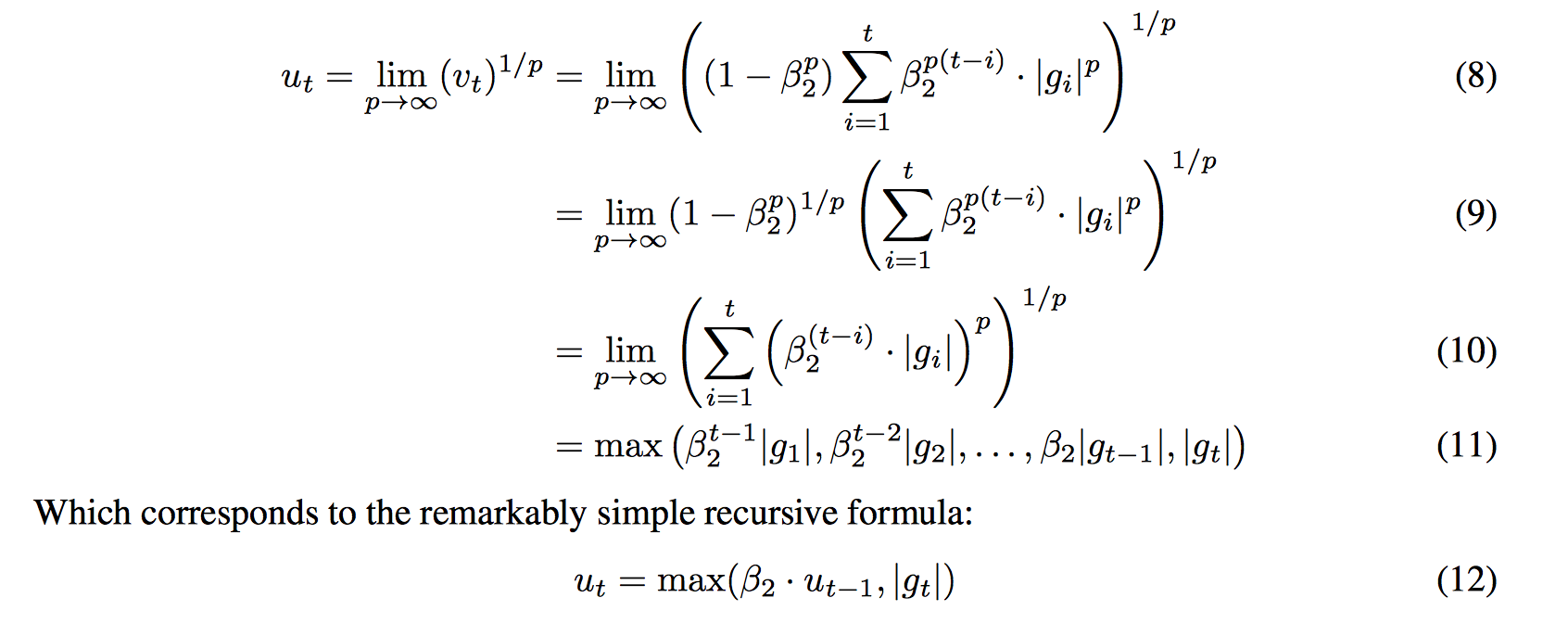
相应的更新权重操作为：

$$\theta_{t+1} = \theta_t -\frac{\eta}{u_t}\hat{m}_t$$

在PyTorch中的实现如下：

# Update biased first moment estimate, which is \hat{m}_t
exp_avg.mul_(beta1).add_(1 - beta1, grad)
# 下面这种用来逐元素求取 max(A, B) 的方法可以学习一个
# Update the exponentially weighted infinity norm.
norm_buf = torch.cat([
    exp_inf.mul_(beta2).unsqueeze(0),
    grad.abs().add_(eps).unsqueeze_(0)
], 0)
## 找到 exp_inf 和 g之间的较大者（只需要在刚刚聚合的这个维度上找即可~）
torch.max(norm_buf, 0, keepdim=False, out=(exp_inf, exp_inf.new().long()))

## beta1 correction
bias_correction = 1 - beta1 ** state['step']
clr = group['lr'] / bias_correction

p.data.addcdiv_(-clr, exp_avg, exp_inf)