来呀，快活呀~

论文 - Learning Structured Sparsity in Deep Neural Networks

发表于

DNN的稀疏化？用L1正则项不就好了？在很多场合，这种方法的确可行。但是当试图使用FPGA/AISC加速DNN的前向计算时，我们希望DNN的参数能有一些结构化的稀疏性质。这样才能减少不必要的cache missing等问题。在这篇文章中，作者提出了一种结构化稀疏的方法，能够在不损失精度的前提下，对深度神经网络进行稀疏化，达到加速的目的。本文作者温伟，目前是杜克大学Chen Yiran组的博士生，做了很多关于结构化稀疏和DNN加速相关的工作。本文发表在NIPS 2016上。本文的代码已经公开：GitHub
SSL的原理示意图

摘要

为了满足DNN的计算速度要求，我们提出了Structure Sparisity Learning (SSL)技术来正则化DNN的“结构”（例如CNN filter的参数，filter的形状，包括channel和网络层深）。它可以带来：

  • 大的DNN —> 紧凑的模型 —> 计算开销节省
  • 硬件友好的结构化稀疏 —> 便于在专用硬件上加速
  • 提供了正则化，提高网络泛化能力 —> 提高了精度

实验结果显示，这种方法可以在CPU/GPU上对AlexNet分别达到平均$5.1$和$3,1$倍的加速。在CIFAR10上训练ResNet，从$20$层减少到$18$层，并提高了精度。

LASSO

SSL是基于Group LASSO的，所以正式介绍文章之前，首先简单介绍LASSO和Group LASSO，
LASSO)(least absolute shrinkage and selection operator)是指统计学习中的特征选择方法。以最小二乘法求解线性模型为例，可以加上L1 norm作为正则化约束，见下式，其中$\beta$是模型的参数。具体推导过程可以参见wiki页面。

而Group LASSO就是将参数分组，进行LASSO操作。

这里只是简单介绍一下LASSO。SSL下面还会详细介绍，不必过多执着于LASSO。

结构化稀疏

DNN通常参数很多，计算量很大。为了减少计算开销，目前的研究包括：稀疏化，connection pruning, low rank approximation等。然而前两种方法只能得到随机的稀疏，无规律的内存读取仍然制约了速度。下面这种图是一个例子。我们使用了L1正则进行稀疏。和原模型相比，精度损失了$2$个点。虽然稀疏度比较高，但是实际加速效果却很差。可以看到，在conv3，conv4和conv5中，有的情况下反而加速比是大于$1$的。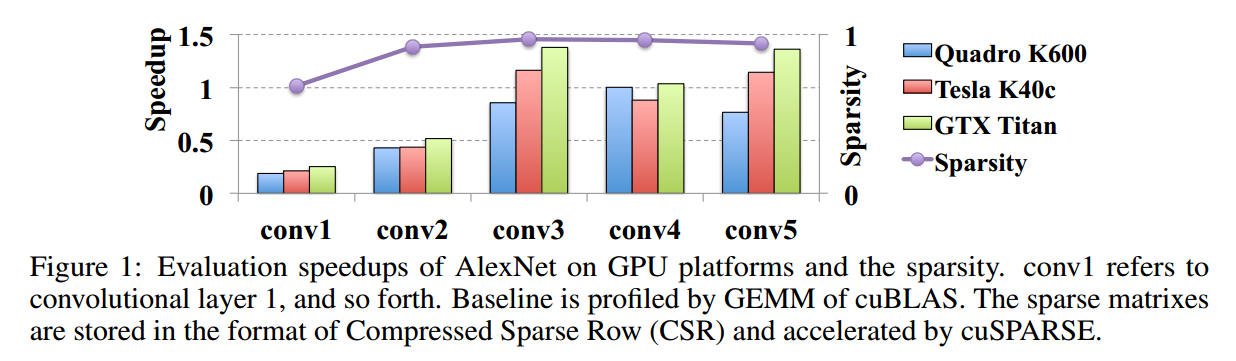
随机稀疏的实际加速效果

low rank approx利用矩阵分解，将预训练好的模型的参数分解为小矩阵的乘积。这种方法需要较多的迭代次数，同时，网络结构是不能更改的。

基于下面实验中观察的事实，我们提出了SSL来直接学习结构化稀疏。

  • 网络中的filter和channel存在冗余
  • filter稀疏化为别的形状能够去除不必要的计算
  • 网络的深度虽然重要，但是并不意味着深层的layer对网络性能一定是好的

假设第$l$个卷积层的参数是一个$4D$的Tensor，$W^{(l)}\in R^{N_l \times C_l \times M_l \times N_l}$，那么SSL方法可以表示为优化下面这个损失函数：

这里，$W$代表DNN中所有权重的集合。$E_D(W)$代表在训练集上的loss。$R$是非结构化的正则项，例如L2 norm。$R_g$是指结构化稀疏的正则项，注意是逐层计算的。对于每一层来说（也就是上述最后一项求和的每一项），group LASSO可以表示为：

其中，$w^{(g)}$是该层权重$W^{(l)}$的一部分，不同的分组可以重叠。$G$是分组的组数。$\Vert \cdot \Vert_g$指的是group LASSO，这里使用的是$\Vert w^{(g)}\Vert_g = \sqrt{\sum_{i=1}^{|w^{(g)}|}(w_i^{(g)})^2}$，也就是$2$范数。

SSL

有了上面的损失函数，SSL就取决于如何对weight进行分组。对不同的分组情况分类讨论如下。图示见博客开头的题图。

惩罚不重要的filter和channel

假设$W^{(l)}_{n_l,:,:,:}$是第$n$个filter，$W^{(l)}_{:, c_l, :,:}$是所有weight的第$c$个channel。可以通过下面的约束来去除相对不重要的filter和channel。注意，如果第$l$层的weight中某个filter变成了$0$，那么输出的feature map中就有一个全$0$，所以filter和channel的结构化稀疏要放到一起。下面是这种形式下的损失函数。为了简单，后面的讨论中都略去了正常的正则化项$R(W)$。

任意形状的filter

所谓任意形状的filter，就是将filter中的一些权重置为$0$。可以使用下面的分组方法：

网络深度

损失函数如下：

不过要注意的是，某个layer被稀疏掉了，会切断信息的流通。所以受ResNet启发，加上了short-cut结构。即使SSL移去了该layer所有的filter，上层的feature map仍然可以传导到后面。

两类特殊的稀疏规则

特意提出下面两种稀疏规则，下面的实验即是基于这两种特殊的稀疏结构。

2D filter sparsity

卷积层中的3D卷积可以看做是2D卷积的组合（做卷积的时候spatial和channel是不相交的）。这种结构化稀疏是将该卷积层中的每个2D的filter，$W^{(l)}_{n_l,c_l,:,:}$，看做一个group，做group LASSO。这相当于是上述filter-wise和channel-wise的组合。

filter-wise和shape-wise的组合加速GEMM

在Caffe中，3D的权重tensor是reshape成了一个行向量，然后$Nl$个filter的行向量堆叠在一起，就成了一个2D的矩阵。这个矩阵的每一列对应的是$W^{(l)}{:,c_l,m_l,k_l}$，称为shape sparsity。两者组合，矩阵的零行和零列可以被抽去，相当于GEMM的矩阵行列数少了，起到了加速的效果。

实验

分别在MNIST，CIFAR10和ImageNet上做了实验，使用公开的模型做baseline，并以此为基础使用SSL训练。

LeNet&MLP@MNIST

分别使用Caffe中实现的LeNet和MLP做实验。

LeNet

限制SSL为filter-wise和channel-wise稀疏化，来惩罚不重要的filter。下表中，LeNet-1是baseline，2和3是使用不同强度得到的稀疏化结果。可以看到，精度基本没有损失($0.1%$)，但是filter和channel数量都有了较大减少，FLOP大大减少，加速效果比较明显。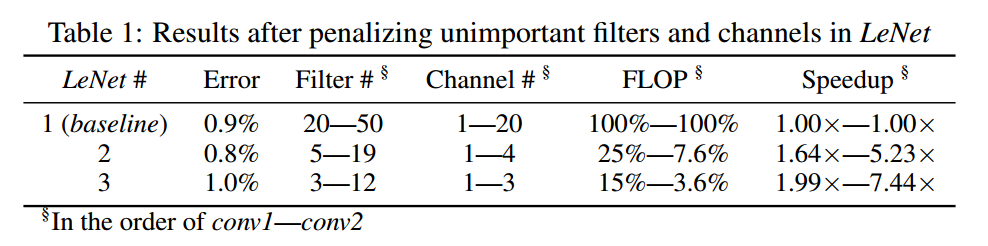
实验结果1

将网络conv1的filter可视化如下。可以看到，对于LeNet2来说，大多数filter都被稀疏掉了。
LeNet的实验结果