CS229 简单的监督学习方法

回过头去复习一下基础的监督学习算法，主要包括最小二乘法和logistic回归。

最小二乘法

最小二乘法是一个线性模型，即：

$$\hat{y} = h_\theta(x) = \sum_{i=1}^{m}\theta_i x_i = \theta^T x$$

定义损失函数为Mean Square Error(MSE)，如下所示。其中，不戴帽子的$y$表示给定的ground truth。

$$J(\theta) = \frac{1}{2}(\hat{y}-y)^2$$

那么，最小二乘就是要找到这样的参数$\theta^*$，使得：

$$\theta^* = \arg\min J(\theta)$$

梯度下降

使用梯度下降方法求解上述优化问题，我们有：

$$\theta_{i+1} = \theta_{i} - \alpha \nabla_\theta J(\theta)$$

求导，有：

$$\begin{aligned}\nabla_\theta J(\theta) &= \frac{1}{2}\nabla_\theta (\theta^T x - y)^2 \\ &= (\theta^T x - y) x\end{aligned}$$

由于这里的损失函数是一个凸函数，所以梯度下降方法能够保证到达全局的极值点。

上面的梯度下降只是对单个样本来做的。实际上，我们可以取整个训练集或者训练集的一部分，计算平均损失函数$J(\theta) = \frac{1}{N}\sum_{i=1}^{N}J_i(\theta)$，做梯度下降，道理是一样的，只不过相差了常数因子$\frac{1}{N}$。

正则方程

除了梯度下降方法之外，上述问题还存在着解析解。我们将所有的样本输入$x^{(i)}$作为行向量，构成矩阵$X \in \mathbb{R}^{N\times d}$。其中，$N$为样本总数，$d$为单个样本的特征个数。那么，对于参数$\theta\in\mathbb{R}^{d\times 1}$来说，$X\theta$的第$i$行就可以给出模型对第$i$个样本的预测结果。我们将ground truth排成一个$N\times 1$的矩阵，那么，损失函数可以写作：

$$J(\theta) = \frac{1}{2N} \Vert X\theta-y \Vert_2^2$$

将$\Vert x\Vert_2^2$写作$x^T x$，同时略去常数项，我们有：

$$\begin{aligned}J &= (X\theta - y)^T (X\theta - y) \\ &= \theta^T X^T X\theta - 2\theta^T x^T y +y^T y\end{aligned}$$

对其求导，有：

$$\nabla_\theta J = X^T X\theta - X^T y$$

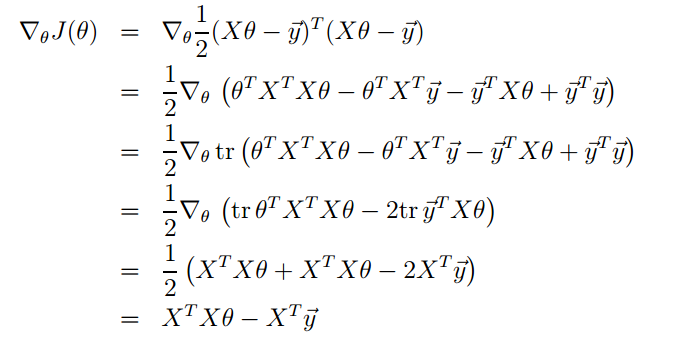
这其中，主要用到的矩阵求导性质如下：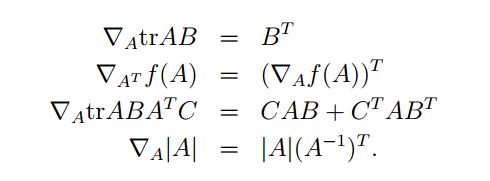

令导数为$0$，求得极值点处：

$$\theta^* = (X^TX)^{-1}X^T y$$

概率解释

这里对上述做法给出一个概率论上的解释。首先我们要引入似然函数（likelihood function）的概念。

似然函数是一个关于模型参数$\theta$的函数，它描述了某个参数$\theta$下，给出输入$x$，得到输出$y$的概率。用具体的公式表示如下：

$$L(\theta) = \prod_{i=1}^{N}P(y^{(i)}|x^{(i)};\theta)$$

假设线性模型的预测结果和ground truth之间的误差服从Gaussian分布，也就是说，

$$y - \theta^T x = \epsilon \sim \mathcal{N}(0, \sigma^2)$$

那么上面的似然函数可以写作：

$$L(\theta) = \prod_{i=1}^{N}\frac{1}{\sqrt{2\pi\sigma}}\exp(\frac{(y^{(i)}-\theta^T x^{(i)})^2}{2\sigma^2})$$

如何估计参数$\theta$呢？我们可以认为，参数$\theta$使得出现样本点$(x^{(i)}, y^{(i)})$的概率变大，所以才能被我们观测到。自然，我们需要使得似然函数$L(\theta)$取得极大值，也就是说：

$$\theta^* = \arg\max L(\theta)$$

通过引入$\log(\cdot)$，可以将连乘变成连加，同时不改变函数的单调性。这样，实际上我们操作的是对数似然函数$\log L(\theta)$。有：

$$\begin{aligned} \mathcal{l} &= \log L(\theta) \\ &= \sum_{i=1}^{N}\log \frac{1}{\sqrt{2\pi\sigma^2}} \exp (\frac{(y^{(i)}-\theta^T x^{(i)})^2}{2\sigma^2})\\ &= N\log\frac{1}{\sqrt{2\pi\sigma^2}} -\frac{1}{\sigma^2}\frac{1}{2}\sum_{i=1}^{N}(y^{(i)}-\theta^T x^{(i)})^2 \end{aligned}$$

略去前面的常数项不管，后面一项正好是最小二乘法的损失函数。要想最大化对数似然函数，也就是要最小化上面的损失函数。

所以，最小二乘法的损失函数可以由数据集的噪声服从Gaussian分布自然地导出。

加权最小二乘法

加权最小二乘法是指对数据集中的数据赋予不同的权重，一个重要的用途是使用权重$w^{(i)} = \exp (-\frac{(x^{(i)}-x)^2}{2\tau^2})$做局部最小二乘。不再多说。

logistic回归

虽然叫回归，但是logistic回归解决的问题是分类问题。

logistic函数

logistic函数$\sigma(x) = \frac{1}{1+e^{-x}}$，又叫sigmoid函数，将输入$(-\infty, +\infty)$压缩到$(0, 1)$之间。它的形状如下：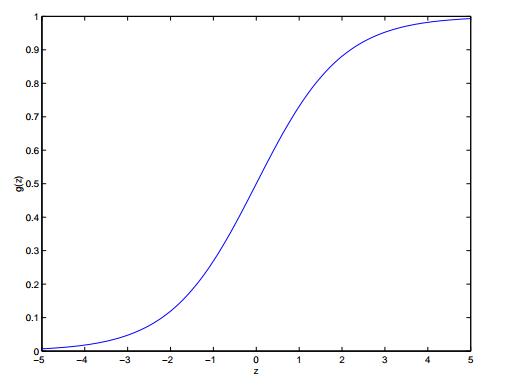

对其求导，发现导数值可以完全不依赖于输入$x$：

$$\frac{d\sigma(x)} {dx} = \sigma(x)(1-\sigma(x))$$

我们将logistic函数的输入取做$x$的feature的线性组合，就得到了假设函数$h_\theta(x) = \sigma(\theta^T x)$。

logistic回归

logistic函数的输出既然是在$(0,1)$上，我们可以将其作为概率。也就是说，我们认为它的输出是样本点属于类别$1$的概率：

$$\begin{aligned}P(y=1|x) &= h_\theta(x) \\ P(y=0|x) &= 1-h_\theta(x) \end{aligned}$$

或者我们写的更紧凑些：

$$P(y|x) = (h_\theta(x))^y (1-h_\theta(x))^{(1-y)}$$

我们仍然使用上述极大似然的估计方法，求取参数$\theta$，为求简练，隐去了上标$(i)$。

$$\begin{aligned}L(\theta) &= \prod_{i=1}^{N}P(y|x;\theta) \\ &=\prod (h_\theta(x))^y (1-h_\theta(x))^{(1-y)} \end{aligned}$$

取对数：

$$\log L(\theta) = \sum_{i=1}^{N}y\log(h(x)) + (1-y)\log(1-h(x))$$

所以，我们的损失函数为$J(\theta) = - [y\log(h(x)) + (1-y)\log(1-h(x))]$。把$h(x)$换成$P$，岂不就是深度学习中常用的交叉损失熵在二分类下的特殊情况？

回到logistic回归，使用梯度下降，我们可以得到更新参数的策略：

$$\theta_{i+1} = \theta_i - \alpha (h_\theta(x) - y)x$$

啊哈！形式和最小二乘法完全一样。只不过要注意，现在的$h_\theta(x)$已经变成了一个非线性函数。

感知机

在上述logistic回归基础上，我们强制将其输出映射到$\lbrace 1, -1\rbrace$。即将$\sigma(x)$换成$g(x)$：

$$g(x) = \begin{cases} 1, \quad\text{if}\quad x \ge 0\\ 0, \quad\text{if}\quad x < 0\end{cases}$$

使用同样的更新方法，我们就得到了感知机模型（perceptron machine）。