简要介绍一下优化方法中的牛顿方法(Newton’s Method)。下面的动图demo来源于Wiki页面。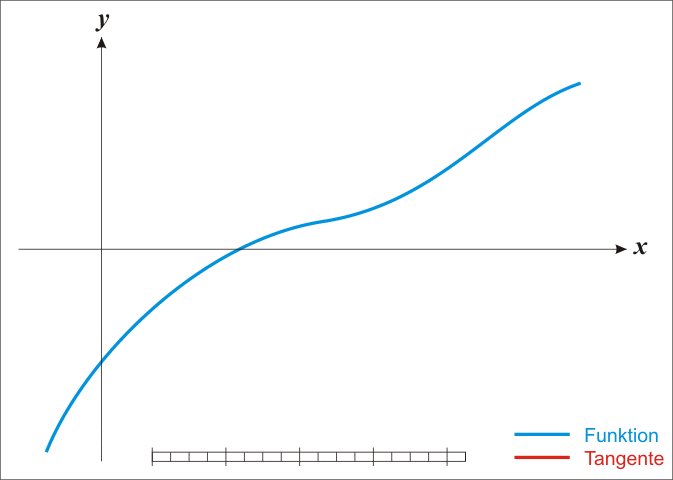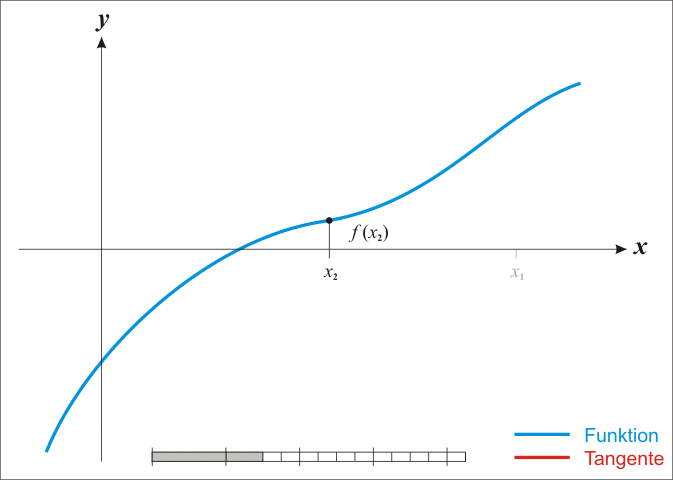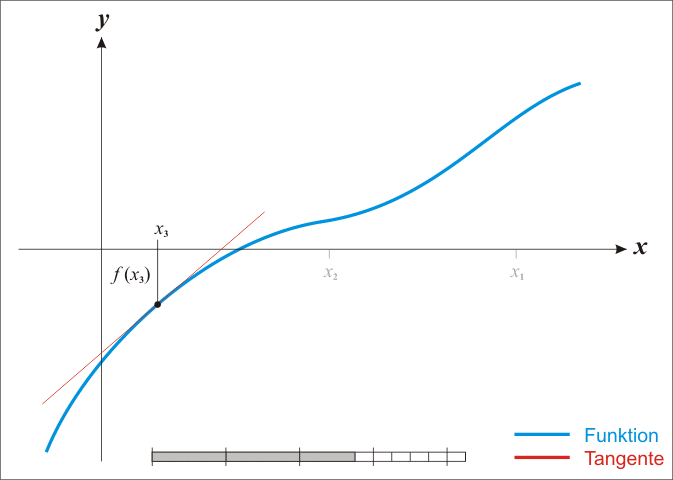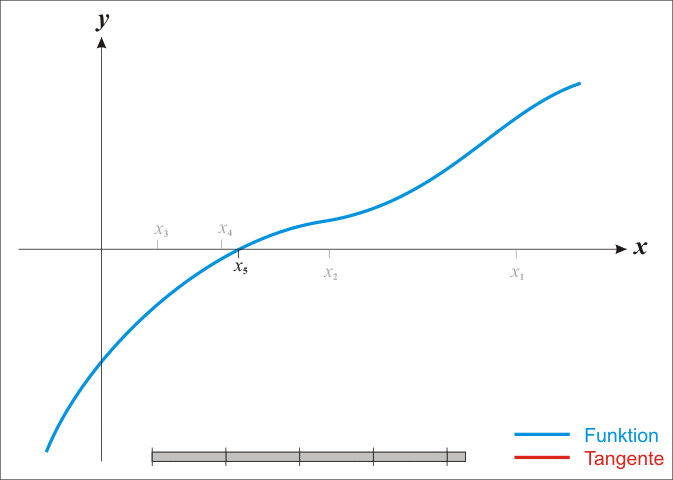
介绍
牛顿方法,是一种用来求解方程$f(x) = 0$的根的方法。从题图可以看出它是如何使用的。
首先,需要给定根的初始值$x_0$。接下来,在函数曲线上找到其所对应的点$(x_0, f(x_0))$,并过该点做切线交$x$轴于一点$x_1$。从$x_1$出发,重复上述操作,直至收敛。
根据图上的几何关系和导数的几何意义,有:
优化上的应用
做优化的时候,我们常常需要的是求解某个损失函数$L$的极值。在极值点处,函数的导数为$0$。所以这个问题被转换为了求解$L$的导数的零点。我们有
推广到向量形式
机器学习中的优化问题常常是在高维空间进行,可以将其推广到向量形式:
其中,$H$表示海森矩阵,是一个$n\times n$的矩阵,其中元素为:
特别地,当海森矩阵为正定时,此时的极值为极小值(可以使用二阶的泰勒展开式证明)。
PS:忘了什么是正定矩阵了吗?想想二次型的概念,对于$\forall x$不为$0$向量,都有$x^THx > 0$。
优缺点
牛顿方法的收敛速度较SGD为快(二阶收敛),但是会涉及到求解一个$n\times n$的海森矩阵的逆,所以虽然需要的迭代次数更少,但反而可能比较耗时($n$的大小)。
L-BFGS
由于牛顿方法中需要计算海森矩阵的逆,所以很多时候并不实用。大家就想出了一些近似计算$H^{-1}$的方法,如L-BFGS等。
推导过程待续。。。
L-BFGS的资料网上还是比较多的,这里有一个PyTorch中L-BFGS方法的实现:optim.lbfgs。
这里有一篇不错的文章数值优化:理解L-BFGS算法,本博客写作过程参考很多。