论文 - Like What You Like - Knowledge Distill via Neuron Selectivity Transfer

好长时间没有写博客了，国庆假期把最近看的东西整理一下。Like What You Like: Knowledge Distill via Neuron Selectivity Transfer这篇文章是图森的工作，在Knowledge Distilling基础上做出了改进Neural Selectivity Transfer，使用KD + NST方法能够取得SOTA的结果。PS：DL领域的论文名字真的是百花齐放。。。Like what you like。。。感受一下。。。

另外，这篇论文的作者Wang Naiyan大神和Huang Zehao在今年的ECCV 2018上还有一篇论文发表，同样是模型压缩，但是使用了剪枝方法，有兴趣可以关注一下：Data-driven sparse structure selection for deep neural networks。

另另外，其实这两篇文章挂在Arxiv的时间很接近，知乎的讨论帖：如何评价图森科技连发的三篇关于深度模型压缩的文章？有相关回答，可以看一下。DL/CV方法论文实在太多了，感觉Naiyan大神和图森的工作还是很值得信赖的，值得去follow。

Motivation

KD的一个痛点在于其只适用于softmax分类问题。这样，对于Detection。Segmentation等一系列问题，没有办法应用。另一个问题在于当分类类别数较少时，KD效果不理想。这个问题比较好理解，假设我们面对一个二分类问题，那么我们并不关心类间的similarity，而是尽可能把两类分开即可。同时，这篇文章的实验部分也验证了这个猜想：当分类问题分类类别数较多时，使用KD能够取得best的结果。

作者联想到，我们是否可以把CNN中某个中间层输出的feature map利用起来呢？Student输出的feature map要和Teacher的相似，相当于是Student学习到了Teacher提取特征的能力。在CNN中，每个filter都是在和一个feature map上的patch做卷积得到输出，很多个filter都做卷积运算，就得到了feature（map）。另外，当filter和patch有相似的结构时，得到的激活比较大。举个例子，如果filter是Sobel算子，那么当输入image是边缘的时候，得到的响应是最大的。filter学习出来的是输入中的某些模式。当模式匹配上时，激活。这里也可以参考一些对CNN中filter做可视化的研究。

顺着上面的思路，有人提出了Attention Transfer的方法，可以参见这篇文章：Improving the Performance of Convolutional Neural Networks via Attention Transfer。而在NST这篇文章中，作者引入了新的损失函数，用于衡量Student和Teacher对相同输入的激活Feature map的不同，可以说除了下面要介绍的数学概念以外，没有什么难理解的地方。整个训练的网络结构如下所示：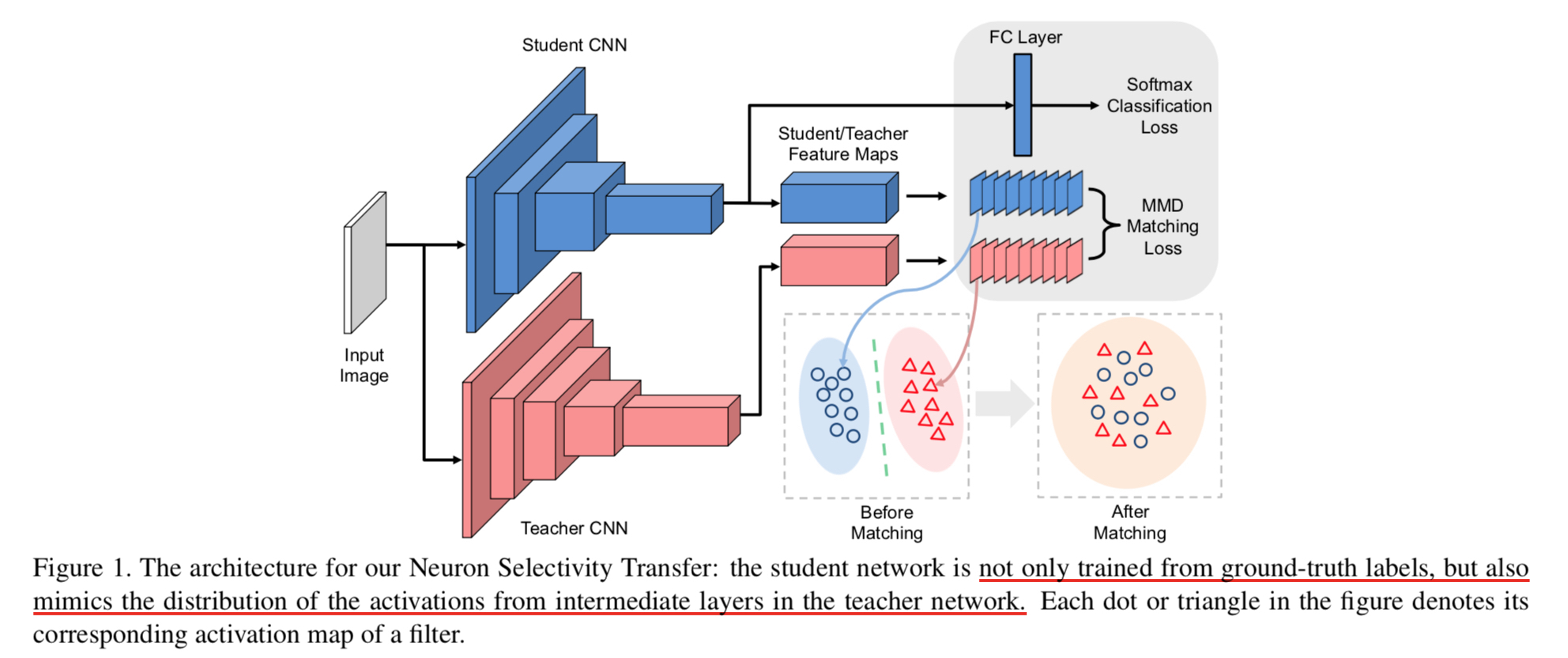

Maximum Mean Discrepancy

MMD 是用来衡量sampled data之间分布差异的距离量度。如果有两个不同的分布$p$和$q$，以及从两个分布中采样得到的Data set$\mathcal{X}$和$\mathcal{Y}$。那么MMD距离如下：

$$\mathcal{L}(\mathcal{X}, \mathcal{Y}) = \Vert \frac{1}{N}\sum_{i=1}^{N}\phi(x^i) - \frac{1}{M}\sum_{j=1}^{M}\phi(y^j) \Vert_2^2$$

其中，$\phi$表示某个mapping function。变形之后（内积打开括号），可以得到：

$$\mathcal{L}(\mathcal{X}, \mathcal{Y}) = \frac{1}{N^2}\sum_{i=1}^{N}\sum_{j=1}^{N}k(x^i, x^j) + \frac{1}{M^2}\sum_{i=1}^{M}\sum_{j=1}^{M}k(y^i, y^j) - \frac{2}{MN}\sum_{i=1}^{N}\sum_{j=1}^{M}k(x^i, y^j)$$

其中，$k$是某个kernel function，$k(x, y) = \phi(x)^{T}\phi(y)$。

我们可以使用MMD来衡量Student模型和Teacher模型中间输出的激活feature map的相似程度。通过优化这个损失函数，使得S的输出分布接近T。通过引入MMD，将NST loss定义如下，下标$S$表示Student的输出，$T$表示Teacher的输出。第一项$\mathcal{H}$是指由样本类别标签计算的CrossEntropy Loss。第二项即为上述的MMD Loss。

$$\mathcal{L} = \mathcal{H}(y, p_S) + \frac{\lambda}{2}\mathcal{L}_{MMD}(F_T, F_S)$$

注意，为了确保后一项有意义，需要保证$F_T$和$F_S$有相同长度。具体来说，对于网络中间输出的feature map，我们将每个channel上的$HW$维的feature vector作为分布$\mathcal{X}$的一个采样。按照作者的设定，我们需要保证S和T对应的feature map在spatial dimension上必须一样大。如果不一样，可以使用插值方法进行扩展。

为了不受相对幅值大小的影响，需要对feature vector做normalization。

对于kernal的选择，作者提出了三种可行方案：线性，多项式和高斯核。在后续通过实验对比了它们的性能。

和其他方法的关联

如果使用线性核函数，也就是$\phi$是一个identity mapping，那么MMD就成了直接比较两个样本分布质心的距离。这时候，和上文提到的AT方法的一种形式是类似的。（这个我觉得有点强行扯关系。。。）

如果使用二次多项式核函数，可以得到，$\mathcal{L}_{MMD}(F_T, F_S) = \Vert G_T - G_S\Vert_F^2$。其中，$G \in \mathbb{R}^{HW\times HW}$为Gram矩阵，其中的元素$g_{ij} = (f^i)^Tf^j$。

实验

作者在CIFAR10，ImageNet等数据集上进行了实验。Student均使用Inception-BN网络，Teacher分别使用了ResNet-1001和ResNet-101。一些具体的参数设置参考论文即可。

下面是CIFAR10上的结果。可以看到，单一方法下，CIFAR10分类NST效果最好，CIFAR100分类KD最好。组合方法中，KD+NST最好。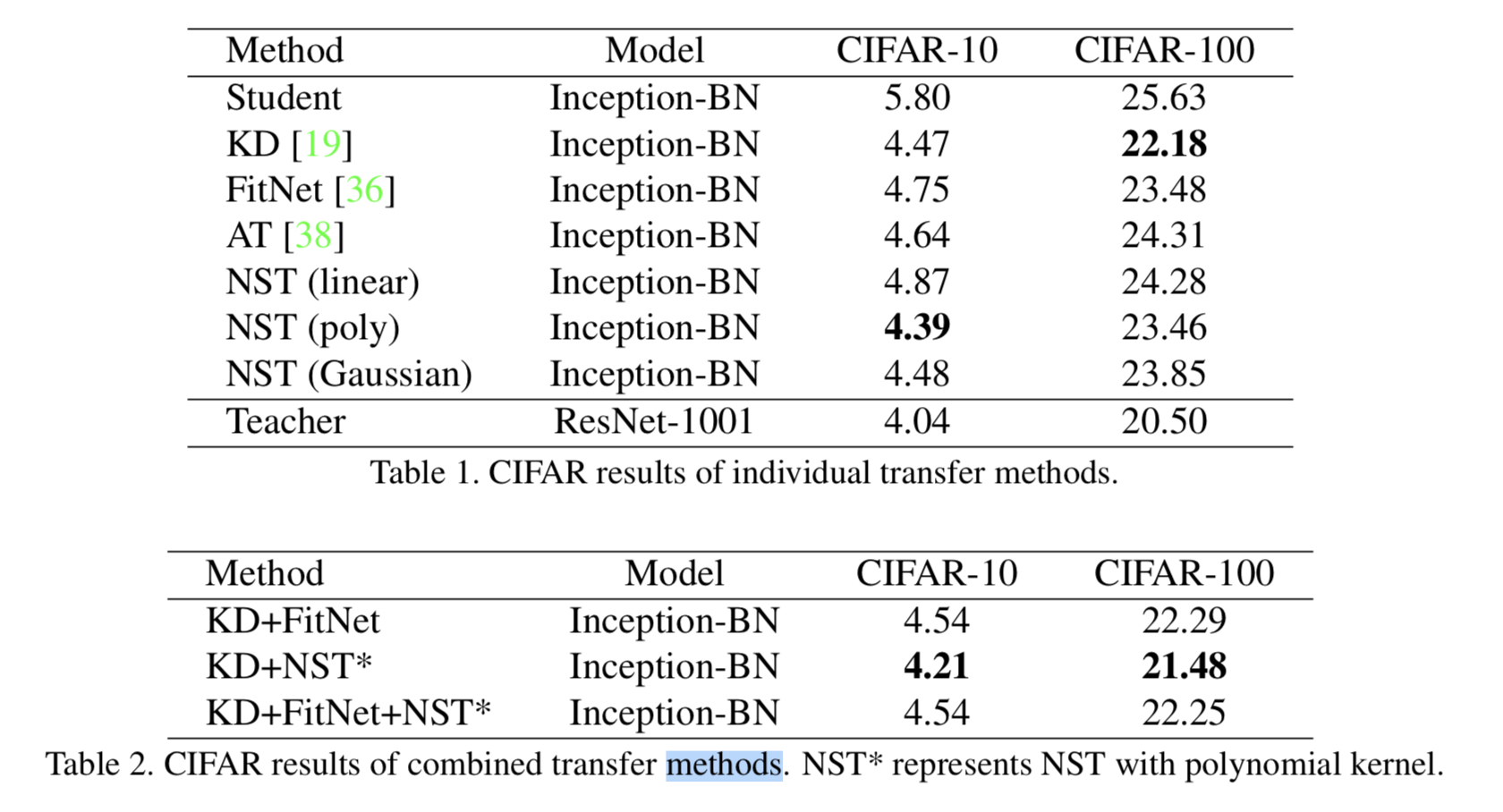

下面是ImageNet上的结果。KD+NST的组合仍然是效果最好的。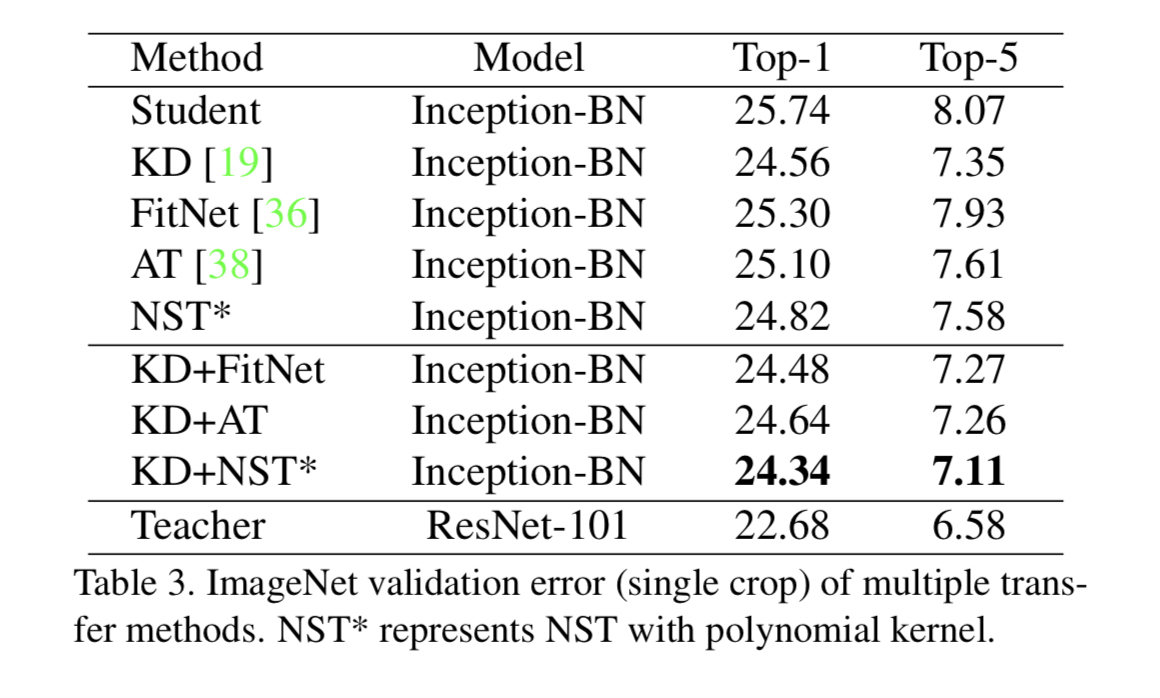

作者还对NST前后，Student和Teacher的输出Feature map做了聚类，发现NST确实能够使得S的输出去接近T的输出分布。如下图所示：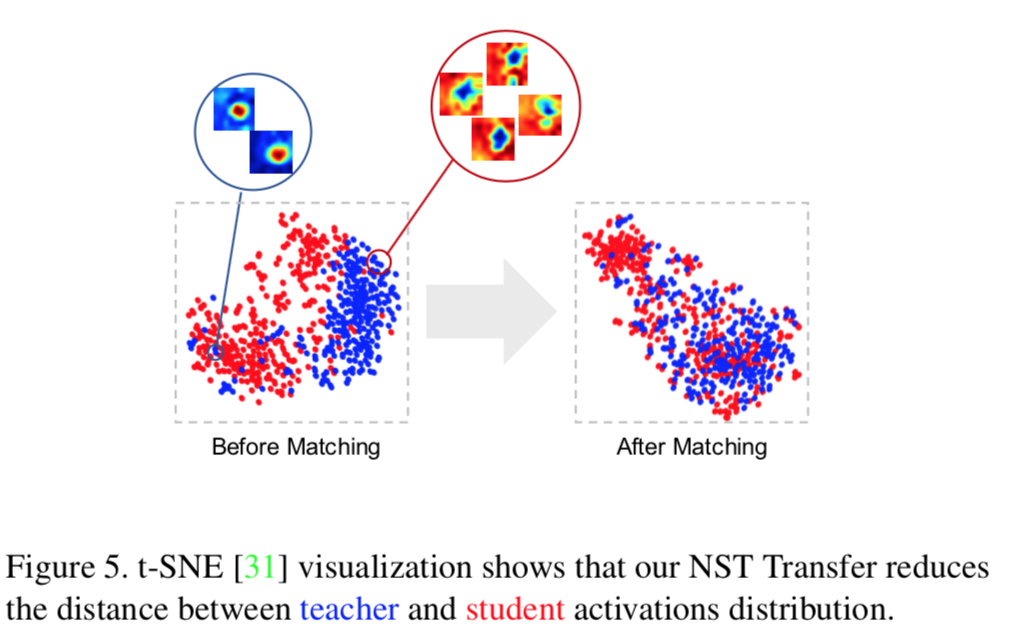

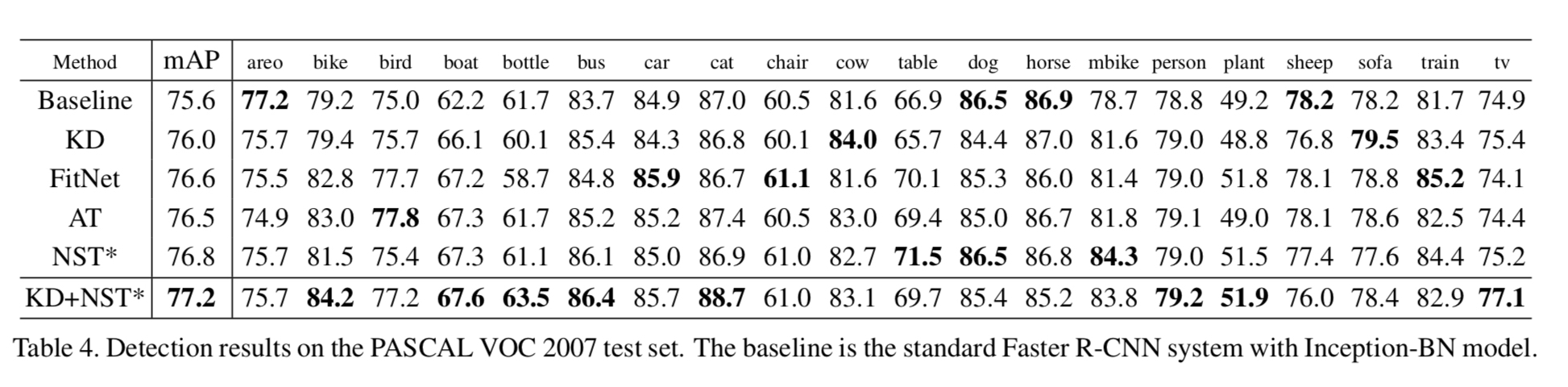
此外，作者还实验了在Detection任务上的表现。在PASCAL VOC2007数据集上基于Faster RCNN方法进行了实验。backbone网络仍然是Inception BN，从4blayer获取feature map，此时stide为16。