论文 - DARTS

NAS的文章很多了，这篇介绍DARTS：DARTS: DIFFERENTIABLE ARCHITECTURE SEARCH

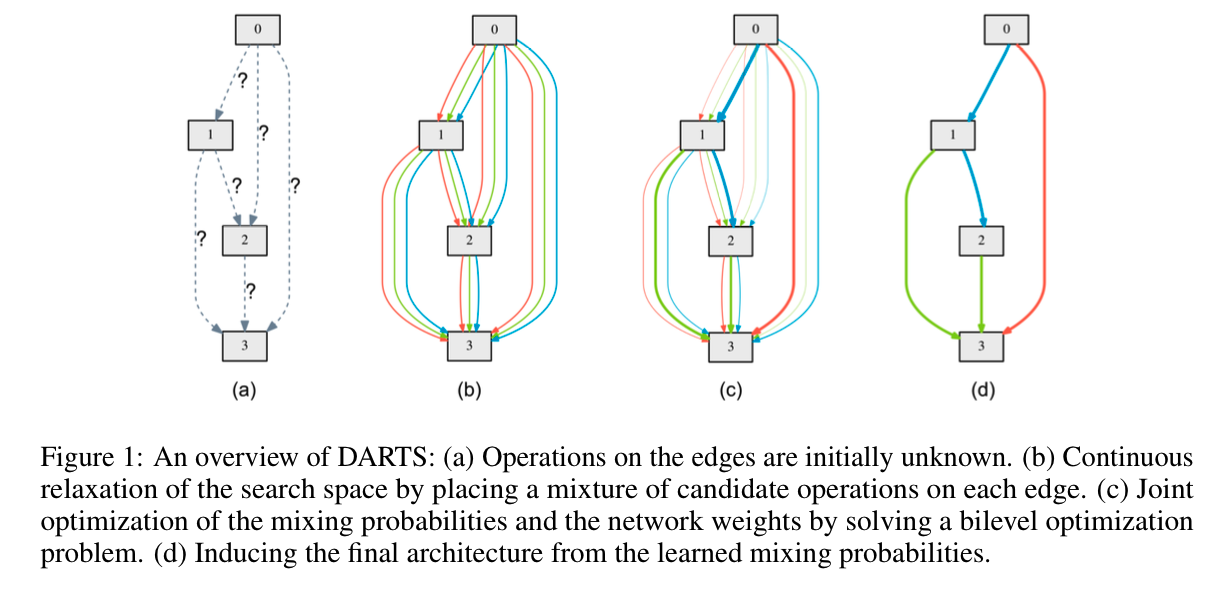
搜索空间

基本沿用前人工作的基本设定：

• 每个cell是由$N$个有序的节点组成的DAG。其中，每个节点$x^{(i)}$表示一个feature map，节点之间的有向弧$E(i,j)$表示由$x^{(i)}$到$x^{(j)}$的某种操作（operation）$o^{(i,j)}$
• 每个cell有两个输入，一个输出。两个输入分别是第$i-1$个和$i-2$个cell的输出（假设当前cell是第$i$个）。输出是cell内所有节点应用某种Reduction操作（如concat）得到的
• 每个节点的值是由它前面的所有节点决定的：

$$x^{(j)} = \sum_{i<j}o^{(i,j)}x^{(i)}$$

• 特殊op“Zero”，表示两个节点之间其实没有连接。

遵循上面的设定，网络结构的搜索，就转换为了搜索节点之间operation的问题。下面，我们就对这个问题建模，将它转换为一个可微分用梯度下降搜索的优化问题。

松弛

“松弛”是一种优化中常用的技巧。

设搜索空间内的所有可能op的集合为$\mathcal{O}$。本来$x^{(i)}$到$x^{(j)}$的op是在这个集合中离散地取值，但是现在我们把它松弛为一个连续问题：

$$\bar{o} = \sum_{o\in\mathcal{O}}\frac{\exp(\alpha_o)}{\sum_{o^{\prime}\in\mathcal{O}}\exp(\alpha_{o^{\prime}})}o$$

其中，$\alpha$是一个长度为$|\mathcal{O}|$的向量，$\alpha_o$是里面对应于操作$o$的权重。

当搜索过程结束后，选取$\mathcal{O}$中能够使得$\alpha$中分量最大的那个元素$o^\ast$就是最终两个节点的连接op：

$$o^{\ast} =\underset{o\in\mathcal{O}}{\operatorname{argmax}} \alpha_o$$

当然，除了网络结构，我们还需要去学习网络的权重参数$w$。所以整个问题是一个bi-level的优化问题，$\alpha$是upper-level变量，$w$是lower-level变量。PS：超参数搜索也有相关工作将其建模为bi-level的优化问题求解。

也就是说，给定某个$\alpha$（也就是某个确定的网络结构），在训练集上得到最优的$w$，并将当前的网络结构和权重在验证集上做评估。那个在验证集上得到最好的结果对应的网络结构，就是我们要找的$\alpha$，而网络的权重$w$也对应得出。

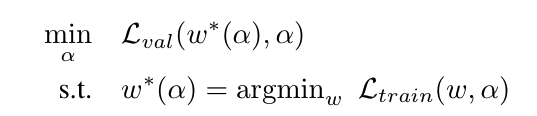
也就是说，我们需要最小化模型在验证集上的损失函数；其中，$w$是$\alpha$的某个函数（在这里，$\alpha$是和某个网络结构一一对应的），需要满足训练集上的损失函数最小。

求解

我们已经把DARTS抽象成了一个优化问题，下面考虑如何高效求解。

显然，按照上面的想法，给定网络结构后，在训练集上得到最优的$w$，再去验证集上跑评估，是不现实的。一是搜索空间巨大，耗时太长；二是仍然无法根据当前的$\alpha$，得到下一步该向哪里走，难道仍然要用启发式或诸如进化算法等方法？如果是求导，那这个链路也太长了，根本不现实。这里作者指出，可以用如下的方式近似梯度：

看起来括号里面的内容是把求解$w^\ast$的$N$步迭代只取了一步。

$$w^\ast = w - \sum_{N}\xi\frac{\partial\mathcal{L}_{\text{train}}(w,\alpha)}{\partial w}|_{w_i}$$

为什么能这样近似？似乎没有什么严密的理论支撑，作者对这个“瑕疵”的处理方法是：

• 拿出CIFAR10和ImageNet以及PTB等数据集上的结果，证明算法在实际上是可以work的，而且效果很好
• 后面给出了一个在简单优化问题上的讨论
• 给出了关于超参数设置的经验技巧，最重要的还放出了源码

这无疑让整个文章的可信度大大增强。

算法迭代步骤可以描述如下：

不过上面的算法描述在实际中并不好用，因为$\alpha$的那一坨梯度一看就很不好求。我们可以通过链式求导法则将其展开。

考虑函数$f(x, g(x))$对$x$的导数$\frac{df}{dx}$。首先令$y = g(x)$，有全微分：

$$df = \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy$$

而且，有$dy = \frac{dg}{dx} dx$。所以，

$$\frac{df}{dx} = \frac{\partial f}{\partial x} + \frac{\partial f}{\partial y} \frac{dg}{dx}$$

回归我们的问题，令$x = \alpha$，$w^\prime = g(\alpha) = w - \xi\nabla_w\mathcal{L}_{train}(w, \alpha)$。

有

$$\frac{dw^\prime}{d\alpha} = -\xi \nabla^2_{w,\alpha}\mathcal{L}_{train}(w,\alpha)$$

将它代回上面$\frac{df}{dx}$，就得到了论文里面的形式：

化简还没有结束。考虑到$\nabla_w\mathcal{L}_{train}$已经是一个$\mathbb{R}^n$的向量，再对$\alpha$求导，就是一个雅克比矩阵。再和后面那个梯度向量相乘，导致计算量很大。这里作者采用了差分近似微分的方法：

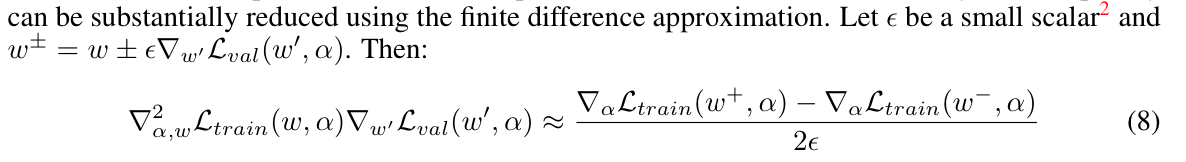
下面是作者的具体计算代码：

# 更新 \alpha
architect.step(input, target, input_search, target_search, lr, optimizer, unrolled=args.unrolled)
# 更新w
optimizer.zero_grad()

下面进入Architect类的内部看下step的实现。当令$\xi=0$时，$w$不用前进一步，architect.step比较简单（对应于unrolled=False）:

def _backward_step(self, input_valid, target_valid):
  # loss = L_val(w, alpha)
  loss = self.model._loss(input_valid, target_valid)
  loss.backward()

当$\xi\neq 0$时，$w$要在train集合上前进一步，对应于unrolled=True：

def _backward_step_unrolled(self, input_train, target_train, input_valid, target_valid, eta, network_optimizer):
  # 在train上更新w = w - \xi * dL_train(w, alpha) / dw
  unrolled_model = self._compute_unrolled_model(input_train, target_train, eta, network_optimizer)
  # 在target上计算loss，然后对alpha求导
  unrolled_loss = unrolled_model._loss(input_valid, target_valid)

  unrolled_loss.backward()
  dalpha = [v.grad for v in unrolled_model.arch_parameters()]
  vector = [v.grad.data for v in unrolled_model.parameters()]
  # 就是那个差分替代微分的式子
  implicit_grads = self._hessian_vector_product(vector, input_train, target_train)
  
  for g, ig in zip(dalpha, implicit_grads):
    g.data.sub_(eta, ig.data)

  # 更新alpha
  for v, g in zip(self.model.arch_parameters(), dalpha):
    if v.grad is None:
      v.grad = Variable(g.data)
    else:
      v.grad.data.copy_(g.data)

差分的计算具体是这里。注意到作者提到了两个超参数的经验值：

def _hessian_vector_product(self, vector, input, target, r=1e-2):
  # R = \epsilon，按照上面的经验值公式求取
  R = r / _concat(vector).norm()
  # 这是前面那一项
  for p, v in zip(self.model.parameters(), vector):
    p.data.add_(R, v)
  loss = self.model._loss(input, target)
  grads_p = torch.autograd.grad(loss, self.model.arch_parameters())

  # 这是后面那一项
  for p, v in zip(self.model.parameters(), vector):
    p.data.sub_(2*R, v)
  loss = self.model._loss(input, target)
  grads_n = torch.autograd.grad(loss, self.model.arch_parameters())

  # 别忘把w复原
  for p, v in zip(self.model.parameters(), vector):
    p.data.add_(R, v)

  # 最后的近似结果
  return [(x-y).div_(2*R) for x, y in zip(grads_p, grads_n)]

Experiment

算法收敛的讨论

这里并没有数学上的证明保证方法的收敛性。作者也没有回避这一点，并指出，\xi 的选取对于是否收敛很重要。总之，实验效果很好，说明这个近似是可以work的。

While we are not currently aware of the convergence guarantees for our optimization algorithm, in practice it is able to reach a fixed point with a suitable choice of ξ

作者对其做在简单问题下的收敛做了讨论。

CNN @ CIFAR10

operation set

选择$3\times 3$，$5\times 5$的kernel size大小的分离卷积和pooling等，再加上identity和zero。具体可以参考代码：darts/cnn/operations.py。例如，$3\times 3$的分离卷积如下：

# 给定input channel和stride，生成3x3分离卷积
# 'sep_conv_3x3' : lambda C, stride, affine: SepConv(C, C, 3, stride, 1, affine=affine),

# 可以看到是如下更小op的串联：

# relu -> 3x3 seperable conv -> bn -> relu -> 3x3 seperable conv(stride=1) -> bn
class SepConv(nn.Module):
    
  def __init__(self, C_in, C_out, kernel_size, stride, padding, affine=True):
    super(SepConv, self).__init__()
    self.op = nn.Sequential(
      nn.ReLU(inplace=False),
      nn.Conv2d(C_in, C_in, kernel_size=kernel_size, stride=stride, padding=padding, groups=C_in, bias=False),
      nn.Conv2d(C_in, C_in, kernel_size=1, padding=0, bias=False),
      nn.BatchNorm2d(C_in, affine=affine),
      nn.ReLU(inplace=False),
      nn.Conv2d(C_in, C_in, kernel_size=kernel_size, stride=1, padding=padding, groups=C_in, bias=False),
      nn.Conv2d(C_in, C_out, kernel_size=1, padding=0, bias=False),
      nn.BatchNorm2d(C_out, affine=affine),
      )

  def forward(self, x):
    return self.op(x)

主要特点是：

• 顺序为relu -> conv -> bn
• 可分离卷积重复两次

这也是前面NAS文章的惯常操作。

网络结构

在Cell尺度上，每个cell由$N=7$个node组成。输入节点如前所述（有时候可能需要$1\times 1$节点），输出节点是该cell的所有中间节点（不包括input节点）在channel上的concat。

在网络宏观尺度上，cell堆叠形成最后的网络。Cell也被分为normal和reduce两种。后者会对输入节点取stride为$2$，从而downsampling。在网络的$1/3$和$2/3$深度处为reduce cell，其他为normal cell。normal和reduce cell分别有一套共享的$\alpha$参数。从而，整个网络的结构可以被两组$\alpha_{\text{normal}}$和$\alpha_{\text{reduce}}$完全描述。

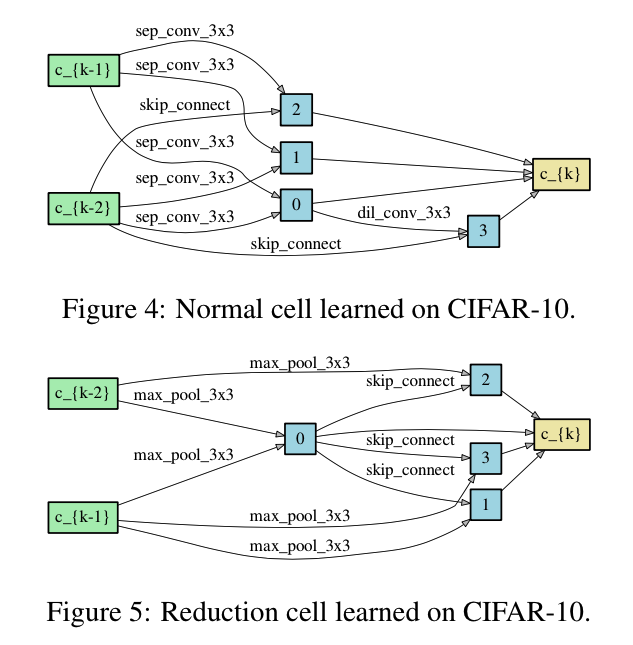
下图直观地展示了在CIFAR10上搜索出来的cell结构：

• 两个输入，一个输出，四个中间节点，它们通过concat操作成了输出
• 每个中间节点入度都是2，也就是我们选取的是$\alpha$中top $K=2$的op

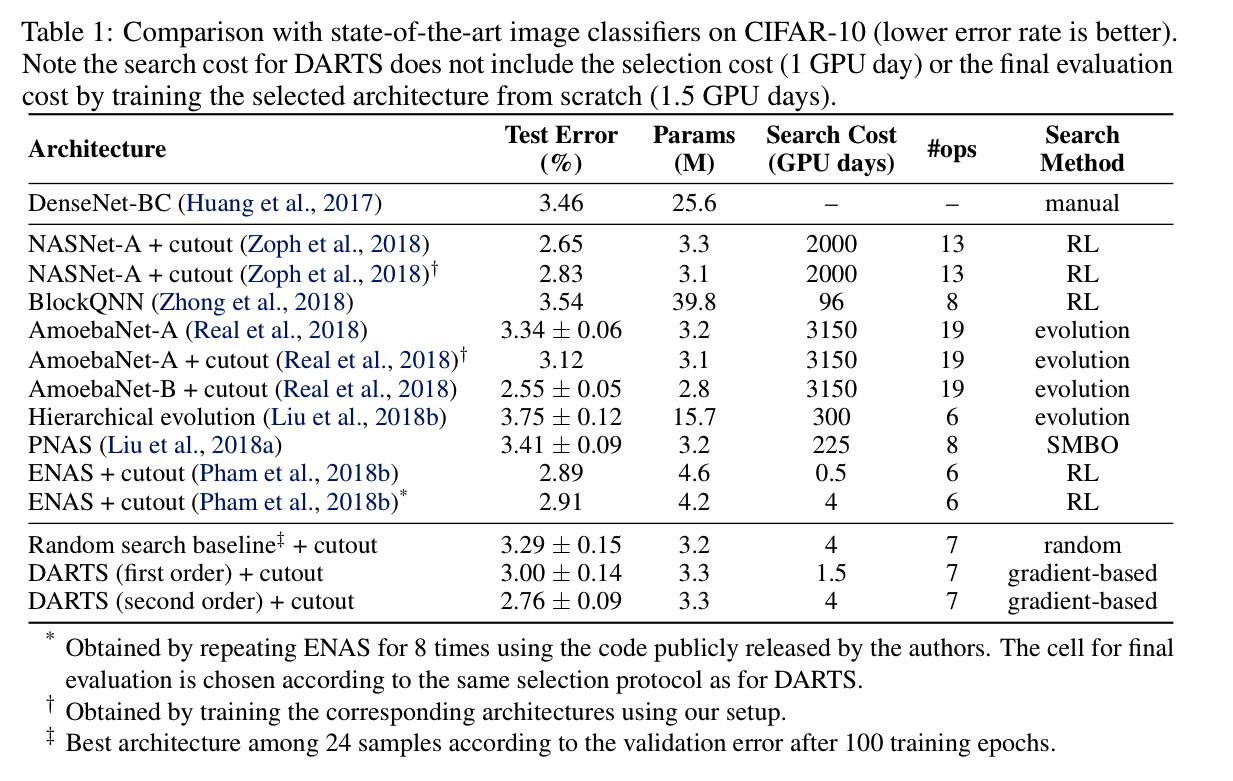
实验结果

在CIFAR10上，搜出的网络性能和之前基于RL或进化算法的SOTA方法是可比的，而且GPU小时数明显缩短。DARTS方法和ENAS是少数能够在<10 GPU*days的计算资源下做出比较好结果的方法。其中DARTS又比ENAS有较好的TestError。作者对此也做了说明：

DARTS outperformed ENAS (Pham et al., 2018b) by discovering cells with comparable error rates but lessparameters. The longer search time is due to the fact that we have repeated the search process fourtimes for cell selection. This practice is less important for convolutional cells however, because theperformance of discovered architectures does not strongly depend on initialization

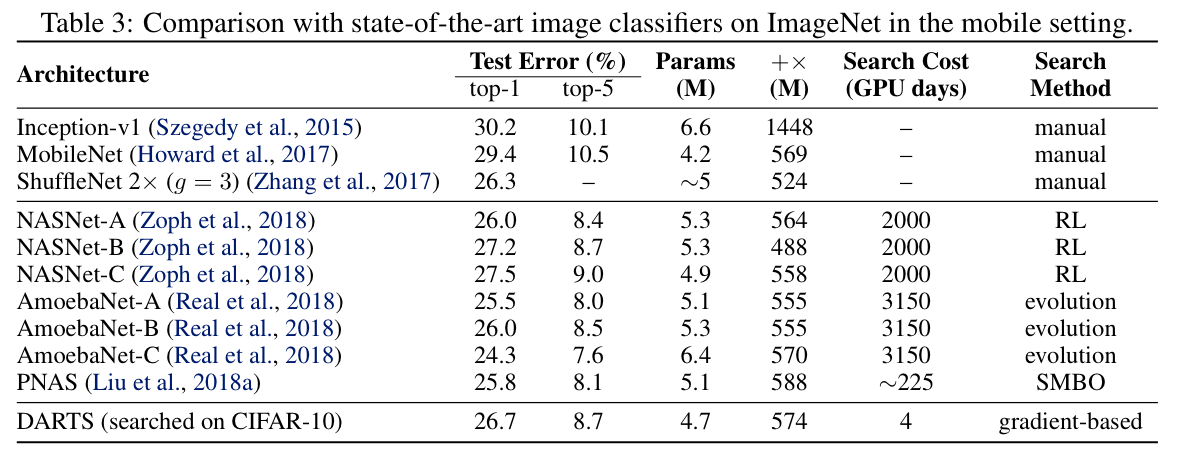
ImageNet

讨论

文章的主要工作：

• 将NAS问题通过松弛建模为一个关于模型结构的优化问题
• 提出了一个不错的解决该优化问题的梯度下降解法
• 在相关任务上证明了方法的有效性
• 给大家在堆GPU资源用强化学习 / 进化算法之外，指出了一条可行的NAS求解之路

文章的作者应该是有比较多的数学优化方面的知识。引入权重向量并softmax求取top K op应该是还算让人容易想到，但后面的优化求解就很容易出错劝退。

参考资料

• PyTorch实现的DARTS：quark0/darts