CS131-线代基础

CS131课程(Computer Vision: Foundations and Applications)，是斯坦福大学Li Feifei实验室开设的一门计算机视觉入门基础课程，该课程目的在于为刚接触计算机视觉领域的学生提供基本原理和应用介绍。目前2016年冬季课程刚刚结束。CS131博客系列主要是关于本课的slide知识点总结与作业重点问题归纳，作为个人学习本门课程的心得体会和复习材料。

2018/03/20 Update: 这门课的2017秋季课程已经全部放出来，和上个版本相比，作业采用Python实现，同时加入了更多机器学习的内容。详细内容见：CS131 Computer Vision@Fall 2017

由于是个人项目，所以会比较随意，只对个人感兴趣的内容做一总结。这篇文章是对课前线代基础的复习与整理。

向量与矩阵

数字图像可以看做二维矩阵，向量是特殊的矩阵，本课程默认的向量都是列向量。
slide中给出了一些矩阵行列式和迹的性质，都比较简单，这里不再多说。

矩阵作为线性变换

通过线代知识，我们知道，在线性空间中，如果给定一组基，线性变换可以通过对应的矩阵来进行描述。

scale变换

对角阵可以用来表示放缩变换。

$$\begin{bmatrix} s_x & 0\\\\ 0 & s_y \end{bmatrix}\begin{bmatrix} x\\\\ y \end{bmatrix} = \begin{bmatrix} s_xx\\\\ s_yy \end{bmatrix}$$

旋转变换

如图所示，逆时针旋转$theta$角度，对应的旋转矩阵为：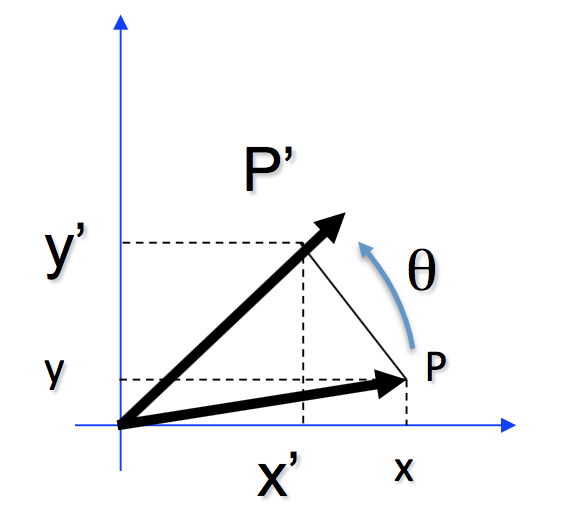

$$\mathbf{R} = \begin{bmatrix} \cos\theta &-\sin\theta \\\\ \sin\theta &\cos\theta \end{bmatrix}$$

旋转矩阵是酉矩阵，矩阵内的各列（或者各行）相互正交。满足如下的关系式：

$$\mathbf{R}\mathbf{R^{\dagger}} = \mathbf{I}$$

由于$\det{\mathbf{R}} = \det{\mathbf{R^{\dagger}}}$，所以，对于酉矩阵，$\det{\mathbf{R}} = \pm 1$
旋转矩阵是酉矩阵，矩阵内的各列（或者各行）相互正交。满足如下的关系式：

$$\mathbf{R}\mathbf{R^{\dagger}} = \mathbf{I}$$

由于$\det{\mathbf{R}} = \det{\mathbf{R^{\dagger}}}$，所以，对于酉矩阵，$\det{\mathbf{R}} = \pm 1$.

齐次变换(Homogeneous Transform)

只用上面的二维矩阵不能表达平移，使用齐次矩阵可以表达放缩，旋转和平移操作。

$$\mathbf{H} =\begin{bmatrix} a & b & t_x\\\\ c & d & t_y\\\\ 0 & 0 & 1 \end{bmatrix},\mathbf{H}\begin{bmatrix} x\\\\ y\\\\ 1\\\\ \end{bmatrix}=\begin{bmatrix} ax+by+t_x\\\\ cx+dy+t_y\\\\ 1 \end{bmatrix}$$

SVD分解

可以将矩阵分成若干个矩阵的乘积，叫做矩阵分解，比如QR分解，满秩分解等。SVD分解，即奇异值分解，也是一种特殊的矩阵分解方法。如下式所示，是将矩阵分解成为三个矩阵的乘积：

$$\mathbf{U}\mathbf{\Sigma}\mathbf{V^\dagger} = \mathbf{A}$$

其中矩阵$\mathbf{A}$大小为$m\times n$，矩阵$\mathbf{U}$是大小为$m\times m$的酉矩阵，$\mathbf{V}$是大小为$n \times n$的酉矩阵，$\mathbf{\Sigma}$是大小为$m \times n$的旋转矩阵，即只有主对角元素不为0.

SVD分解在主成分分析中年很有用。由于矩阵$\mathbf{\Sigma}$一般情况下是将奇异值按照从大到小的顺序摆放，所以矩阵$\mathbf{U}$中，前面的若干列被视作主成分，后面的列显得相对不这么重要。可以抛弃后面的列，进行图像压缩。

如下图，是使用前10个分量对原图片进行压缩的效果。

im = imread('./superman.png');
im_gray = rbg2gray(im);
[u, s, v] = svd(double(im_gray));
k = 10;
uk = u(:, 1:k);
sigma = diag(s);
sk = diag(sigma(1:k));
vk = v(:, 1:k);
im_k = uk*sk*vk';
imshow(uint8(im_k))