CS131-线性滤波器和矩阵的SVD分解

数字图像可以看做$\mathbb{R}^2 \rightarrow \mathbb{R}^c$的映射，其中$c$是图像的channel数。使用信号与系统的角度来看，如果单独考察某个channel，可以将图像看做是二维离散系统。

卷积

卷积的概念不再详述，利用不同的kernel与原始图像做卷积，就是对图像进行线性滤波的过程。卷积操作时，以某一个点为中心点，最终结果是这个点以及它的邻域点的线性组合，组合系数由kernel决定。一般kernel的大小取成奇数。如下图所示。（图片来自博客《图像卷积与滤波的一些知识点》）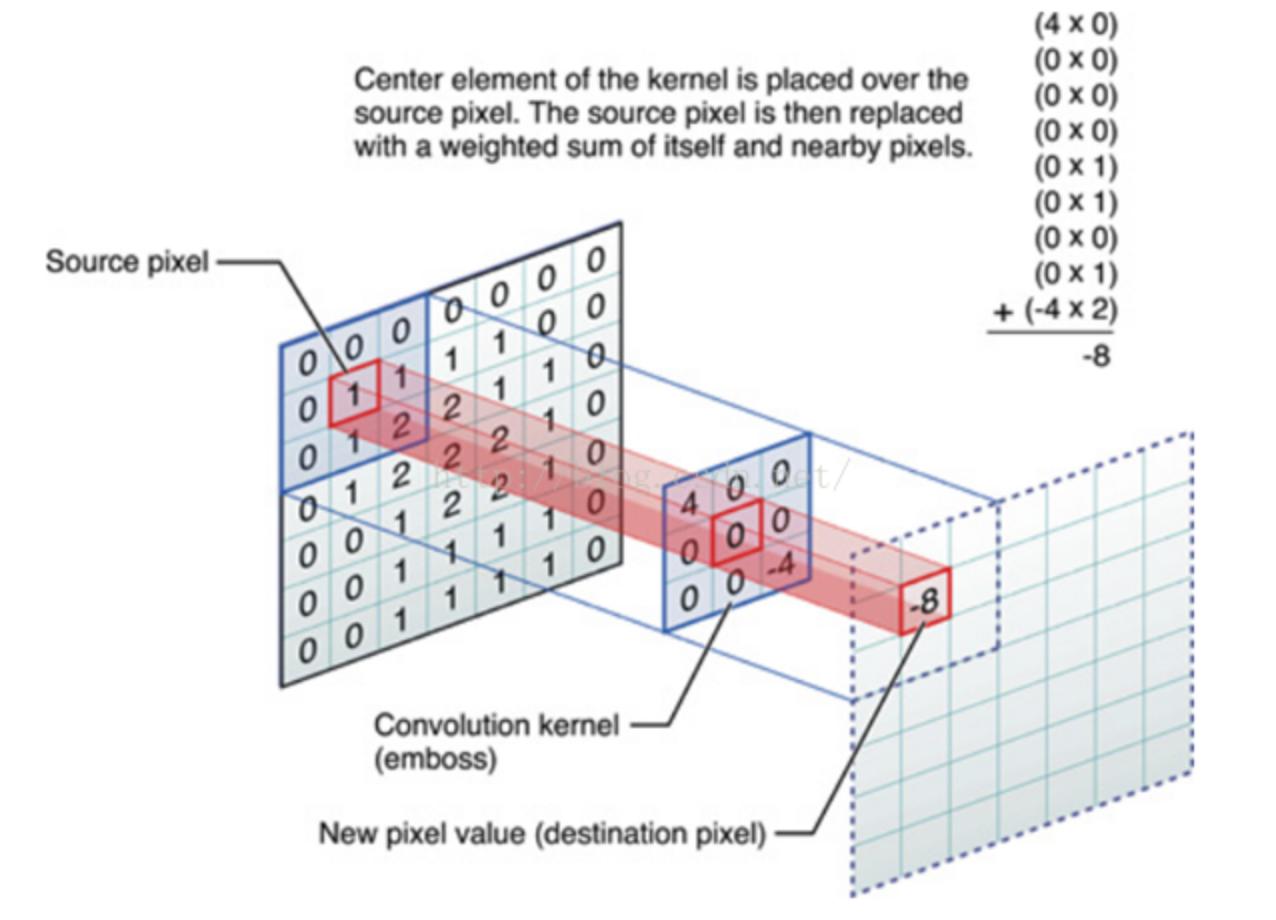

在卷积操作时，常常需要对图像做padding，常用的padding方法有：

• zero padding，也就是填充0值。
• edge replication，也就是复制边缘值进行填充。
• mirror extension，也就是将图像看做是周期性的，相当于使用对侧像素值进行填充。

作业1

调整图像灰度值为0到255

计算相应的k和offset值即可。另外MATLAB中的uint8函数可以将结果削顶与截底为0到255之间。

scale_ratio = 255.0 / (max_val - min_val);
offset = -min_val * scale_ratio;
fixedimg = scale_ratio * dark + offset;

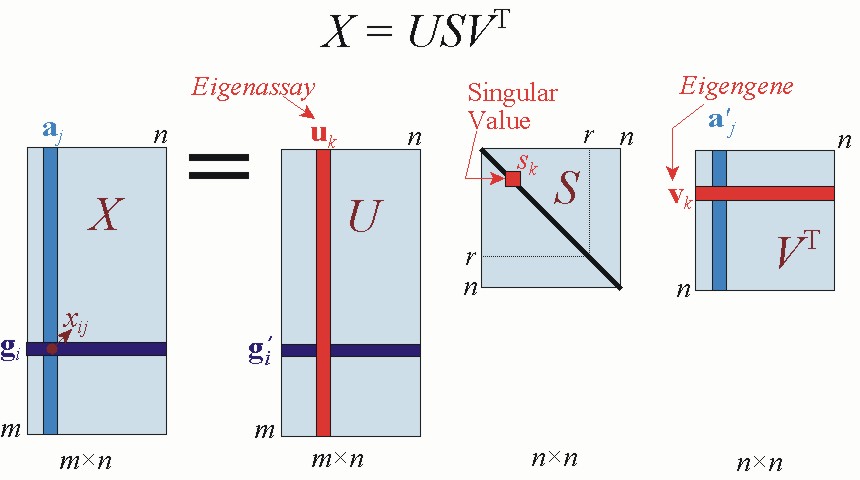
SVD图像压缩

使用SVD进行图像压缩，下图是将所有奇异值按照从大到小的顺序排列的大小示意图。可以看到，第一个奇异值比其他高出一个数量级。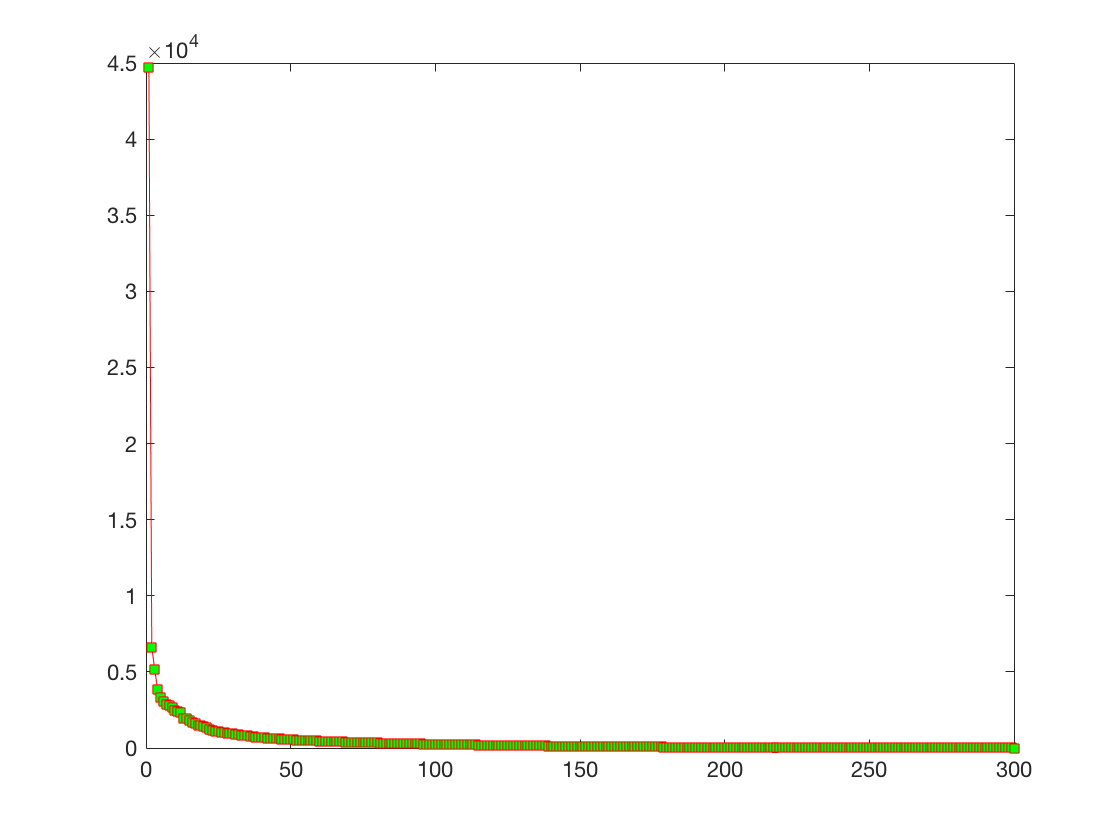

MATLAB实现

分别使用10，50， 100个分量进行图像压缩，如下图所示。可以看到，k=10时，已经能够复原出原图像的大致轮廓。当k更大时，更多细节被复原出来。

MATLAB代码如下：

%% read image
im = imread('./flower.bmp');
im_gray = double(rgb2gray(im));
[u, s, v] = svd(im_gray);
%% get sigular value
sigma = diag(s);
top_k = sigma(1:10);
figure
plot(1:length(sigma), sigma, 'r-', 'marker', 's', 'markerfacecolor', 'g');

figure
subplot(2, 2, 1);
imshow(uint8(im_gray));
title('flower.bmp')
index = 2;
for k = [10, 50, 100]
    uk = u(:, 1:k);
    sk = s(1:k, 1:k);
    vk = v(:, 1:k);
    im_rec = uk * sk * vk';
    subplot(2, 2, index);
    index = index + 1;
    imshow(uint8(im_rec));
    title(sprintf('k = %d', k));
end

图像SVD压缩中的误差分析

完全是个人随手推导，不严格的说明：

将矩阵分块。由SVD分解公式$\mathbf{U}\mathbf{\Sigma} \mathbf{V^\dagger} = \mathbf{A}$，把$\mathbf{U}$按列分块，$\mathbf{V^\dagger}$按行分块，有下式成立：

$$\begin{bmatrix} u_1 & u_2 &\vdots &u_n \end{bmatrix} \begin{bmatrix} \sigma_1 & & & \\\\ & \sigma_2& & \\\\ & & \ddots& \\\\ & & &\sigma_m \end{bmatrix} \begin{bmatrix} v_1^\dagger\\\\ v_2^\dagger\\\\ \dots\\\\ v_m^\dagger \end{bmatrix}=\mathbf{A}$$

由于

$$\begin{bmatrix} u_1 & u_2 &\vdots &u_n \end{bmatrix} \begin{bmatrix} \sigma_1 & & & \\\\ & \sigma_2& & \\\\ & & \ddots& \\\\ & & &\sigma_m \end{bmatrix} = \begin{bmatrix} \sigma_1u_1 & \sigma_2u_2 &\vdots &\sigma_nu_n \end{bmatrix}$$

所以，

$$\mathbf{A} = \sum_{i = 1}^{r}\sigma_iu_iv_i^\dagger$$

上面的式子和式里面只有$r$项，是因为当$k > r$时，$\sigma_k = 0$。

所以$\mathbf{A} - \hat{\mathbf{A}} = \sum_{i = k+1}^{r}\sigma_iu_iv_i^\dagger$

根绝矩阵范数的性质，我们有，

$$\left\lVert\mathbf{A} - \hat{\mathbf{A}}\right\rVert \le \sum_{i=k+1}^{r}\sigma_i\left\lVert u_i\right\rVert\left\lVert v_i^\dagger\right\rVert$$

由于$u_i$和$v_i$都是标准正交基，所以范数小于1.故，

$$\left\lVert\mathbf{A} - \hat{\mathbf{A}}\right\rVert \le \sum_{i=k+1}^{r}\sigma_i$$

取无穷范数，可以知道对于误差矩阵中的任意元素（也就是压缩重建之后任意位置的像素灰度值之差），都有：

$$e \le \sum_{i=k+1}^{r}\sigma_i$$

SVD与矩阵范数

如果某个函数$f$满足以下的性质，就可以作为矩阵的范数。

• $f(\mathbf{A}) = \mathbf{0} \Leftrightarrow \mathbf{A} = \mathbf{0}$
• $f(c\mathbf{A}) = c f(\mathbf{A}), \forall c \in \mathbb{R}$
• $f(\mathbf{A+b}) \le f(\mathbf{A}) + f(\mathbf{B})$

其中，矩阵的2范数可以定义为

$$\left\lVert\mathbf{A}\right\rVert_2 = \max{\sqrt{(\mathbf{A}x)^\dagger\mathbf{A}x}}$$

其中，$x$是单位向量。上式的意义在于表明矩阵的2范数是对于所有向量，经过该矩阵线性变换后摸长最大的那个变换后向量的长度。

下面，给出不严格的说明，证明矩阵的2范数数值上等于其最大的奇异值。

对于空间内的任意单位向量$x$，利用矩阵的SVD分解，有（为了书写简单，矩阵不再单独加粗）：

$$(Ax)^\dagger Ax = x^\dagger V \Sigma^\dagger \Sigma V^\dagger x$$

其中，$U^\dagger U = I$，已经被消去了。

进一步化简，我们将$V^\dagger x$看做一个整体，令$\omega = V\dagger x$，那么有，

$$(Ax)^\dagger Ax = (\Sigma \omega)^\dagger \Sigma \omega$$

也就是说，矩阵的2范转换为了$\Sigma \omega$的幅值的最大值。由于$\omega$是酉矩阵和一个单位向量的乘积，所以$\omega$仍然是单位阵。

由于$\Sigma$是对角阵，所以$\omega$与其相乘后，相当于每个分量分别被放大了$\sigma_i$倍。即

$$\Sigma \omega = \begin{bmatrix} \sigma_1 \omega_1\\\\ \sigma_2 \omega_2\\\\ \cdots\\\\ \sigma_n \omega_n \end{bmatrix}$$

它的幅值平方为

$$\left\lVert \Sigma \omega \right \rVert ^2 = \sum_{i=1}^{n}\sigma_i^2 \omega_i^2 \le \sigma_{1} \sum_{i=1}^{n}\omega_i^2 = \sigma_1^2$$

当且仅当，$\omega_1 = 1$, $\omega_k = 0, k > 1$时取得等号。

综上所述，矩阵2范数的值等于其最大的奇异值。

矩阵的另一种范数定义方法Frobenius norm定义如下：

$$\left\lVert A \right\rVert_{F} = \sqrt{\sum_{i=1}^{m}\sum_{j=1}^{n}\left\vert a_{i,j}\right\rvert}$$

如果我们两边平方，可以得到，矩阵的F范数实际等于某个矩阵的迹，见下式：

$$\left\lVert A\right \rVert_F^2 = \text{trace}(A^\dagger A)$$

利用矩阵的SVD分解，可以很容易得出，$\text{trace}(A^\dagger A) = \sum_{i=1}^{r}\sigma_i^2$

说明如下：

$$\text{trace}(A^\dagger A) = \text{trace}(V\Sigma^\dagger\Sigma V^\dagger)$$

由于$V^\dagger = V^{-1}$，而且$\text{trace}(BAB^{-1}) = \text{trace}(A)$，所以，

$$\text{trace}(A^\dagger A) = \text{trace}(\Sigma^\dagger \Sigma) = \sum_{i=1}^{r}\sigma_i^2$$

也就是说，矩阵的F范数等于它的奇异值平方和的平方根。

$$\left\lVert A\right\rVert_F= \sqrt{\sum_{i=1}^{r}\sigma_i^2}$$