边缘(Edge)在哺乳动物的视觉中有重要意义。在由若干卷积层构成的深度神经网络中,较低层的卷积层就被训练成为对特定形状的边缘做出响应。边缘检测也是计算机视觉和图像处理领域中一个重要的问题。
边缘的产生
若仍采取将图像视作某一函数的观点,边缘是指这个函数中的不连续点。边缘检测是后续进行目标检测和形状识别的基础,也能够在立体视觉中恢复视角等。边缘的来源主要有以下几点:
- 物体表面不平造成灰度值的不连续;
- 深度值不同造成灰度值不连续;
- 物体表面颜色的突变造成灰度值不连续
朴素思想
利用边缘是图像中不连续点的这一性质,可以通过计算图像的一阶导数,再找到一阶导数的极大值,即认为是边缘点。如下图所示,在白黑交界处,图像一阶导数的值非常大,表明此处灰度值变化剧烈,是边缘。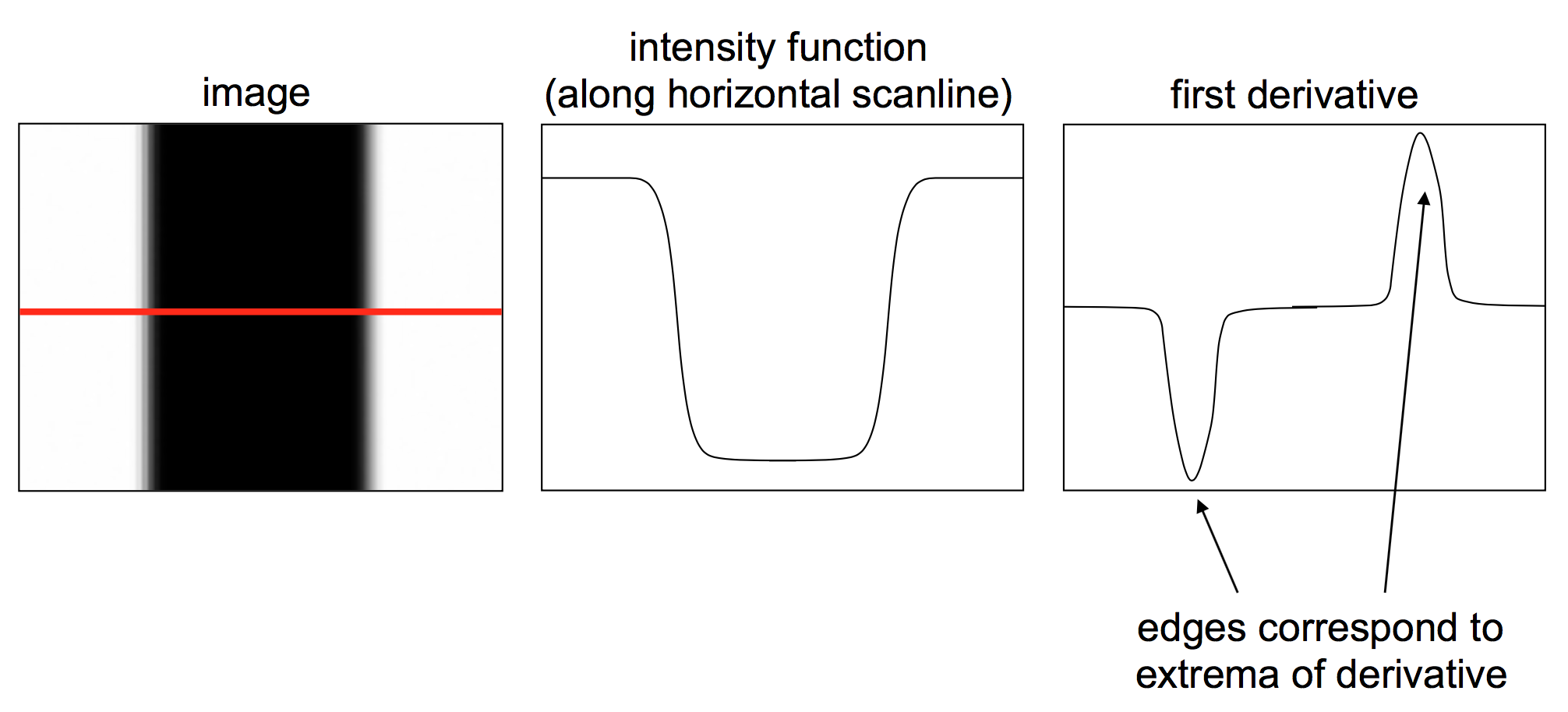
问题转换为如何求取图像的一阶导数(或梯度)。由于图像是离散的二元函数,所以下文不再区分求导与差分。
在$x$方向上,令$g_x = \frac{\partial f}{\partial x}$;在$y$方向上,令$g_y = \frac{\partial f}{\partial y}$。梯度的大小和方向为
通过和Sobel算子等做卷积,可以求取两个正交方向上图像的一阶导数,并计算梯度,之后检测梯度的局部极大值就能够找出边缘点了。
只是这种方法很容易受到噪声影响。如图所示,真实的边缘点被湮没在了噪声中。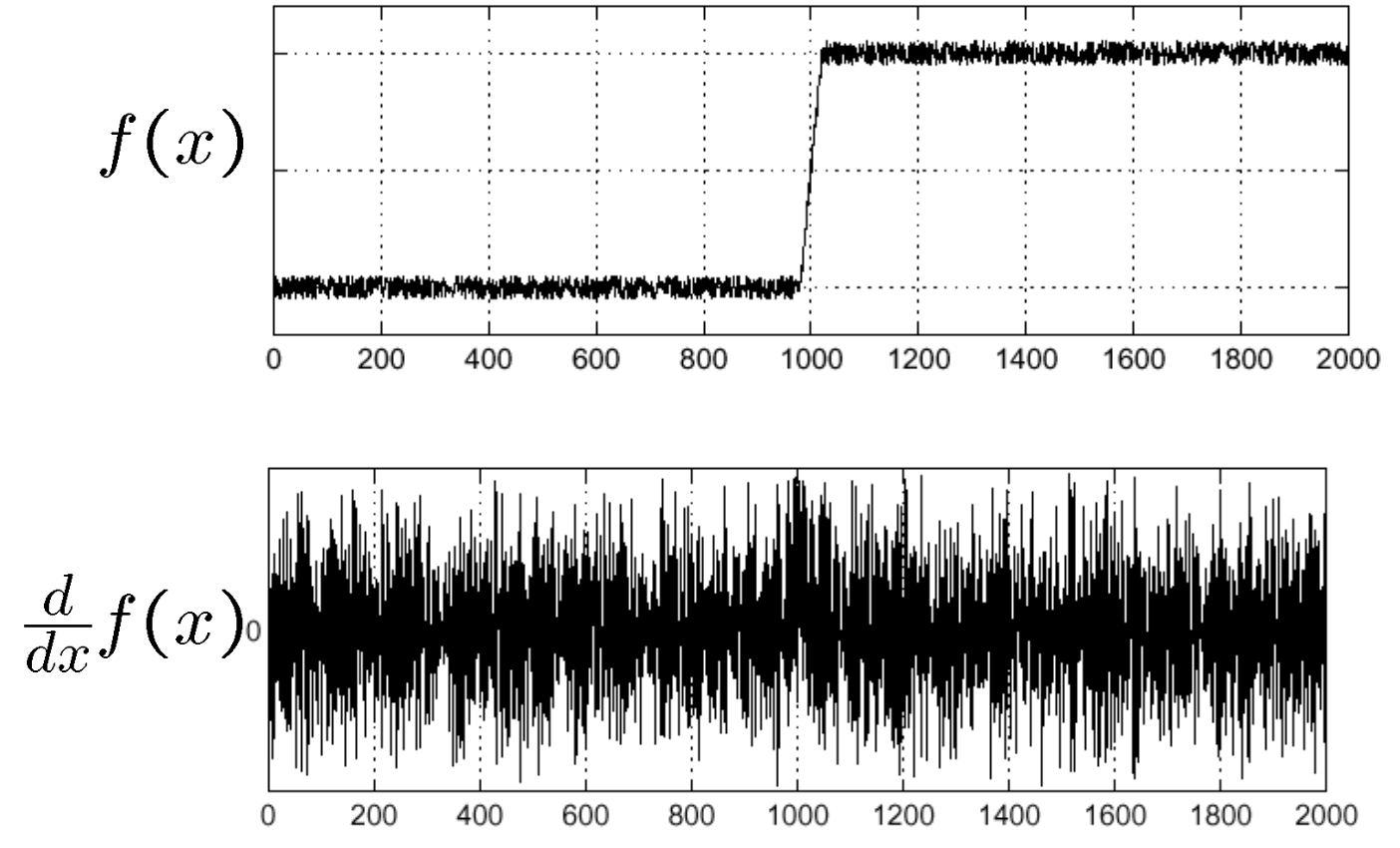
改进1:先平滑
改进措施1,可以首先对图像进行高斯平滑,再按照上面的方法求取边缘点。根据卷积的性质,有:
所以我们可以先求取高斯核的一阶导数,再和原始图像直接做一次卷积就可以一举两得了。这样,引出了DoG(Deriative of Gaussian)。$x$方向的DoG如图所示。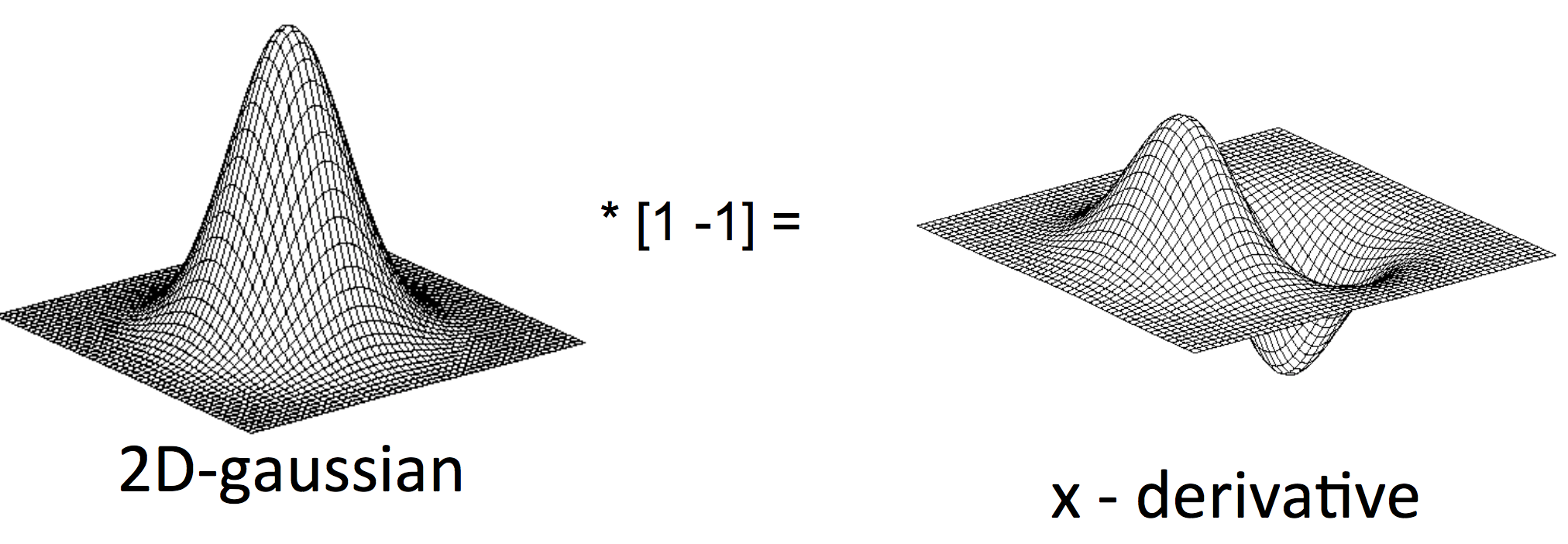
进行高斯平滑不可避免会使图像中原本的细节部分模糊,所以需要在克服噪声和引入模糊之间做好折中。
改进2:Canny检测子
改进措施2,使用Canny检测子进行检测。Canny检测方法同样基于梯度,其基本原理如下:
- 使用DoG计算梯度幅值和方向。
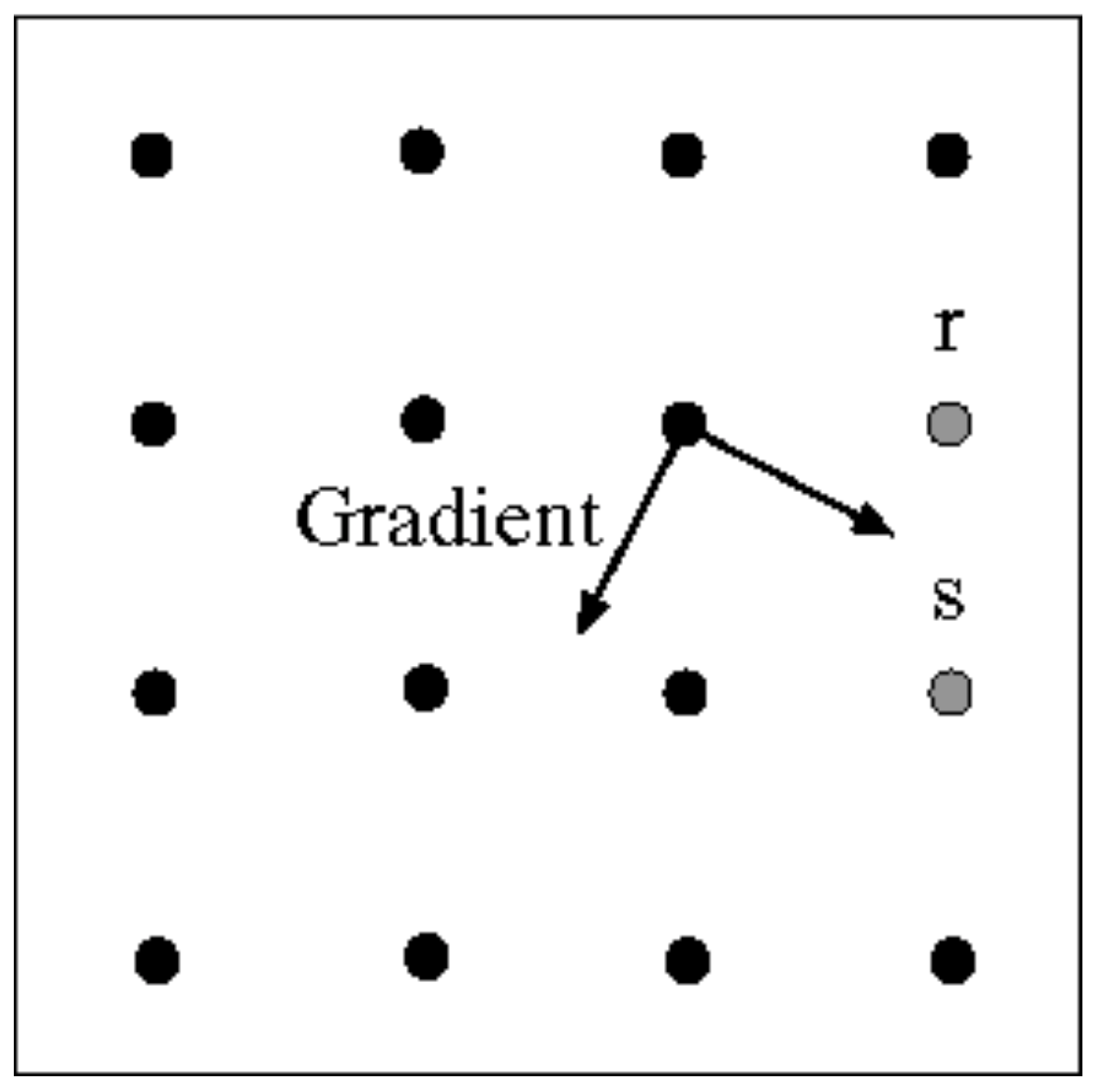
- 非极大值抑制,这个过程需要根据梯度方向做线性插值。如图,沿着点$q$的梯度方向找到了$p$和$r$两个点。这两个点的梯度幅值需要根据其临近的两点做插值得到。
- 利用梯度方向和边缘线互相垂直这一性质,如图,若已经确定点$p$为边缘点,则向它的梯度方向正交方向上寻找下一个边缘点(点$r$或$s$)。这一步也叫edge linking。
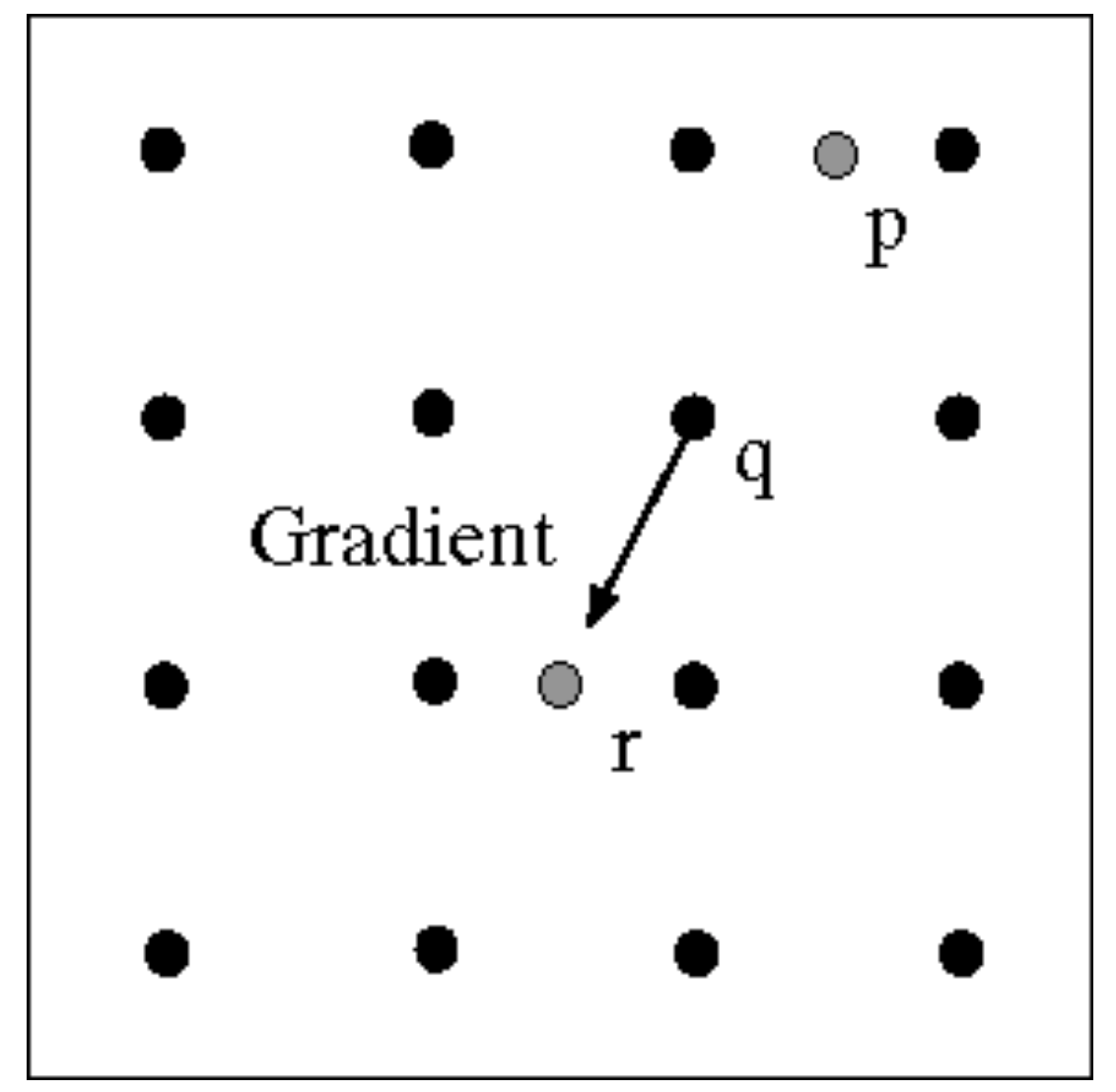
同时,为了提高算法性能,Canny中采用了迟滞阈值的方法,设定low和high两个阈值,来判定某个点是否属于强或弱边缘点。在做edge linking的时候,从强边缘点开始,如果遇到了弱边缘点,则继续,直到某点的梯度幅值甚至比low还要小,则在此停止。
改进3:RANSAC方法
有的时候,我们并不是想要找到所有的边缘点,可能只是想找到图像中水平方向的某些边缘。这时候可以考虑采用RANSAC方法。
RANSAC方法的思想在于,认为已有的feature大部分都是好的。这样,每次随机抽取出若干feature,建立model,再在整个feature集合上进行验证。那么由那些好的feature得到的model一定是得分较高的。(世界上还是好人多啊!)这样就剔除了离群点的影响。
以直线拟合为例,在下图中,给出了使用RANSAC方法拟合直线的步骤。如图1所示,由于离群点的存在,如果直接使用最小二乘法进行拟合,拟合结果效果会很不理想。由于确定一条直线需要两个点,所以从点集中选取两个点,并计算拟合直线。并计算点集中的点在这条直线附近的个数,作为对模型好坏的判定,这些点是新的内点。找出最优的那条直线,使用其所有内点再进行拟合,重复上述操作,直至迭代终止。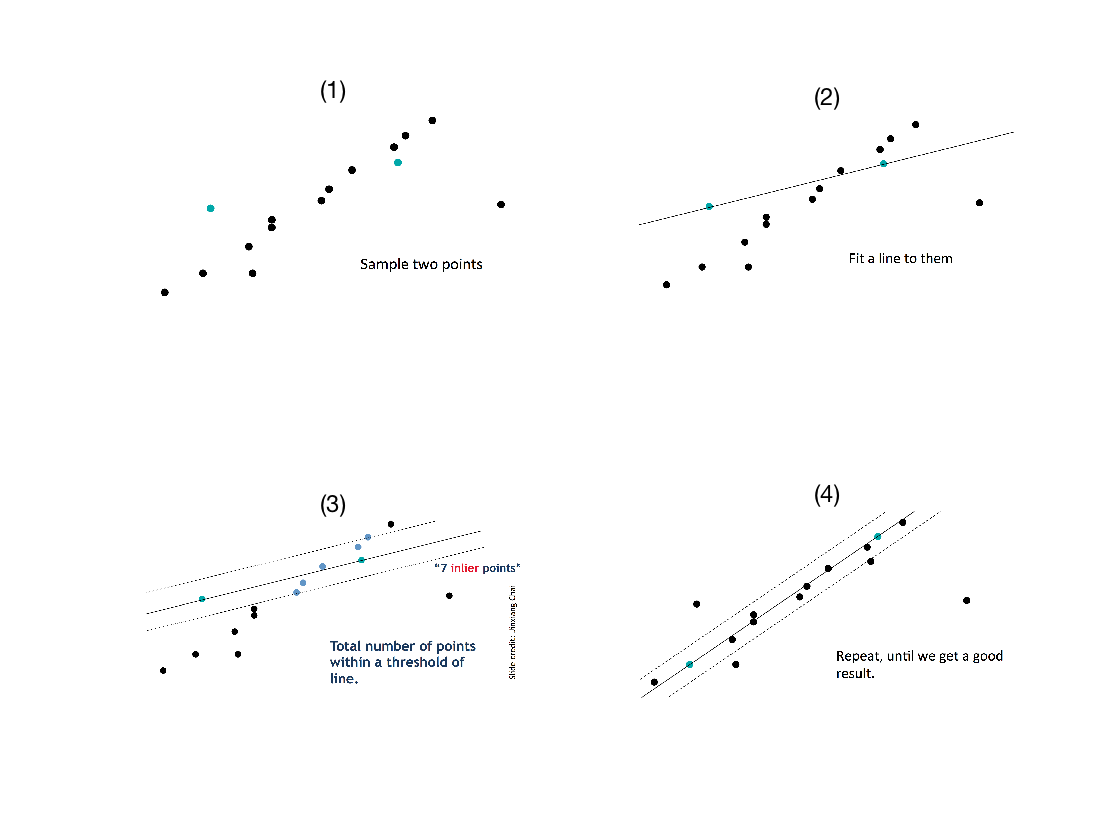
上述RANSAC方法进行直线拟合的过程可以总结如下:
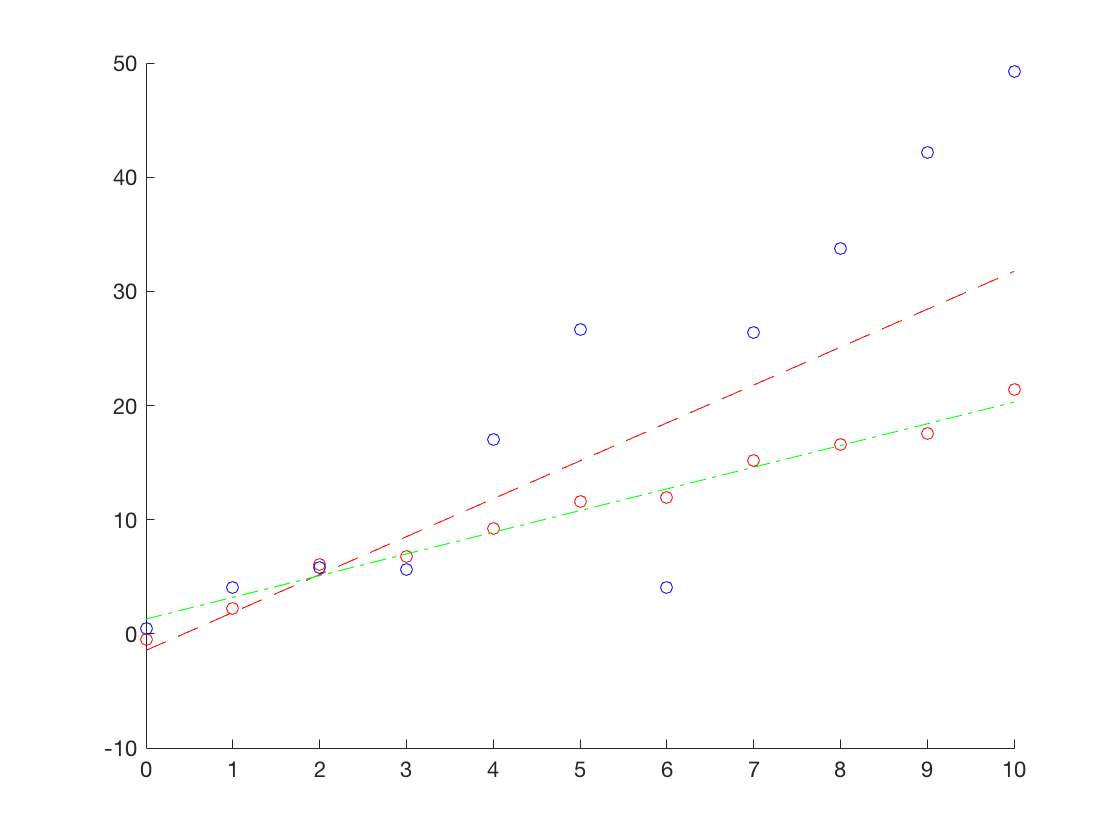
按照上述思想,我分别使用最小二乘法和RANSAC方法尝试进行直线拟合。在下面的代码中,我首先产生了正常受到一定高斯噪声污染的数据(图中的红色点),这些点的真值都落在直线$y = 2x+1$上。而后,我随机变化了斜率和截距,以期产生一些离群点(图中的蓝色点)。当然,由于随机性,这种方法生成的点有可能仍然是内点。
而后,我分别使用上述两种方法进行拟合。可以从结果图中看出,RANSAC(绿色线)能够有效避免离群点的干扰,获得更好的拟合效果。在某次实验中,两种方法的拟合结果如下:1
2least square: a = 3.319566, b = -1.446528
ransac method: a = 1.899640, b= 1.298608
实验使用的MATLAB代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62%% generate data
x = 0:1:10;
y_gt = 2*x+1;
y = y_gt + randn(size(y_gt));
scatter(x, y, [], [1,0,0]);
hold on
out_x = 0:1:10;
out_y = 5*rand(size(out_x)).*out_x + 4*rand(size(out_x));
scatter(out_x, out_y, [], [0,0,1]);
X = [x, out_x]';
Y = [y, out_y]';
X = [X, ones(length(X), 1)];
[a, b] = ls_fit(X, Y);
plot(x, a*x+b, 'linestyle', '--', 'color', 'r');
[ra, rb] = ransac_fit(X, Y, 100, 2, 0.5, 3);
plot(x, ra*x+rb, 'linestyle', '-.', 'color', 'g');
fprintf('least square: a = %f, b = %f\n',a, b);
fprintf('ransac method: a = %f, b= %f\n', ra, rb)
function [a, b] = ransac_fit(X, Y, k, n, t ,d)
% ransac fit
% k -- maximum iteration number
% n -- smallest point numer required
% t -- threshold to identify a point is fit well
% d -- the number of nearby points to assert a model is fine
data = [X, Y];
N = size(data, 1);
best_good_cnt = -1;
best_a = 0;
best_b = 0;
for i = 1:k
% sample point
idx = randsample(N, n);
data_sampled = data(idx, :);
% fit with least square
[a, b] = ls_fit(data_sampled(:, 1:2), data_sampled(:, 3));
% test model
not_sampled = ones(N, 1);
not_sampled(idx) = 0;
not_sampled_data = data(not_sampled == 1, :);
distance = abs(not_sampled_data(:, 1:2) * [a; b] - not_sampled_data(:, 3)) / sqrt(a^2+1);
inner_flag = distance < t;
good_cnt = sum(inner_flag);
if good_cnt >= d && good_cnt > best_good_cnt
best_good_cnt = good_cnt;
data_refine = data(find(inner_flag), :);
[a, b] = ls_fit(data_refine(:, 1:2), data_refine(:, 3));
best_a = a;
best_b = b;
end
fprintf('iteration %d, best_a = %f, best_b = %f\n', i, best_a, best_b);
end
a = best_a;
b = best_b;
end
function [a, b] = ls_fit(X, Y)
% least square fit
A = X'*X\X'*Y;
a = A(1);
b = A(2);
end
我们对RANSAC稍作分析,可以大概了解试验次数$k$的确定方法。
仍然使用上述直线拟合的例子。如果所有点中内点所占的比例为$\omega$,每次挑选$n$个点尝试(上述demo代码中取$n=2$)。那么每次挑选的两个点全部是内点的概率为$\omega^n$。当选取的$n$个点全部为内点时,视为有效实验。那么,重复$k$次实验,有效实验次数为0的概率为$(1-\omega^n)^k$。由于底数小于1,所以我们只需尽量增大$k$,就能够降低这种倒霉的概率。下图是不同$n$和$\omega$情况下为了使得实验成功的概率大于0.99所需的$k$的分布。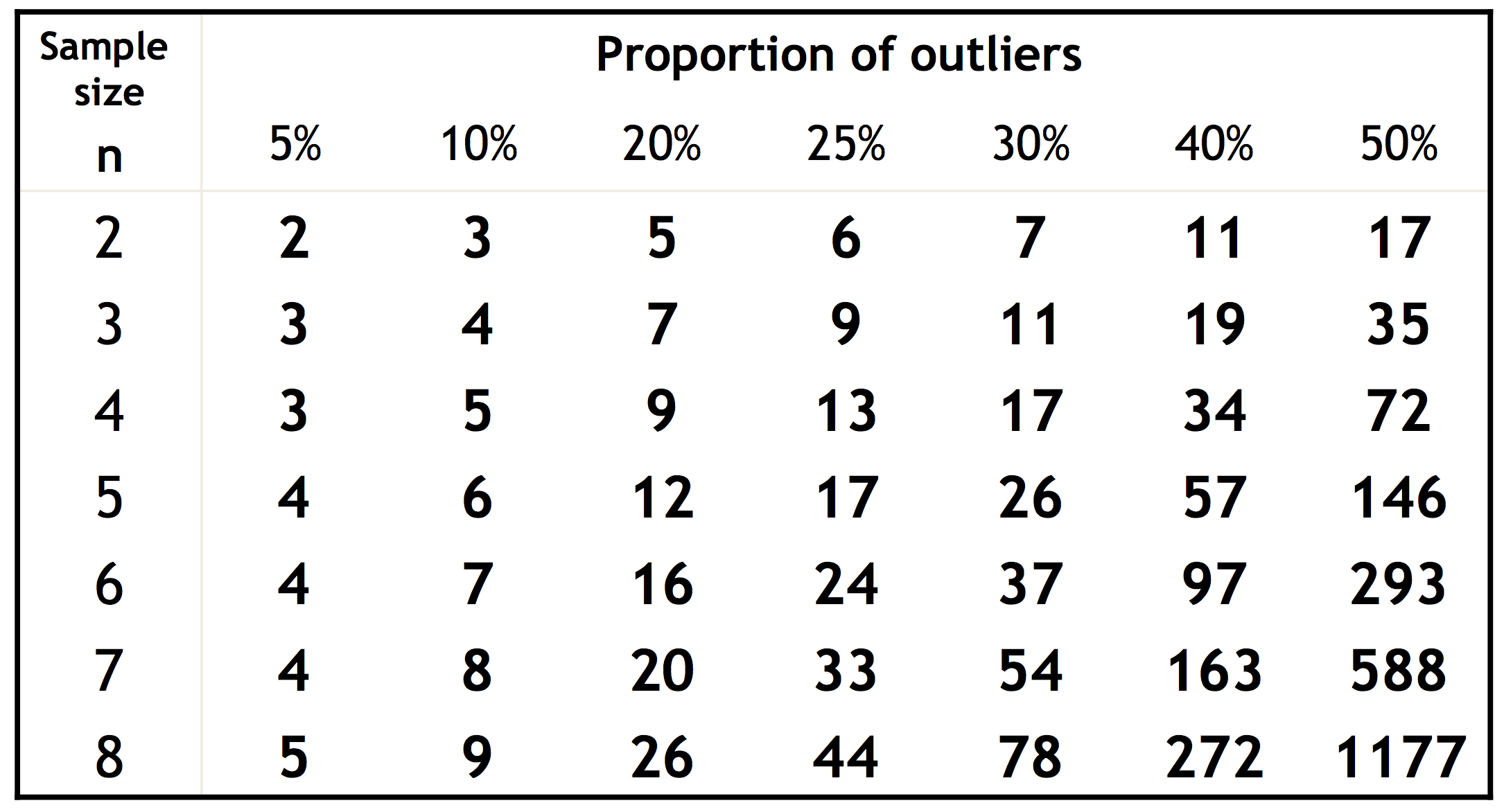
RANSAC方法的有点在于能够较为鲁棒地估计模型的参数,而且实现简单。缺点在于当离群点比例较大时,为保证实验成功所需的$k$值较大。这时候,可能Hough变换等基于投票的方法更适合用于图像中的直线检测问题。
