数字图像是现实世界的物体通过光学成像设备在感光材料上的投影。在3D到2D的转换过程中,深度信息丢失。如何从单幅或者多幅图像中恢复出有用的3D信息,需要使用立体视觉的知识进行分析。如下图所示。这篇博客对课程讲义中立体视觉部分做一整理,分别介绍了针孔相机模型和对极集合的基础知识。
针孔相机模型(Pinhole Camera)
针孔相机是简化的相机模型。光线沿直线传播。物体反射的光线,通过针孔,在成像面形成倒立的影像。针孔与成像面的距离,称为焦距。一般而言,针孔越小,影像越清晰,但针孔太小,会导致衍射,反而令影像模糊。
投影几何的重要性质
在对针孔相机详细说明之前,首先介绍投影几何(Projective Geometry)的几条性质。
在投影变换前后,长度和角度信息丢失,但直线仍然保持是直线。如下图所示。原来垂直和平行的台球桌面的边不再保持原有的角度和相对长度,但是仍然是直线。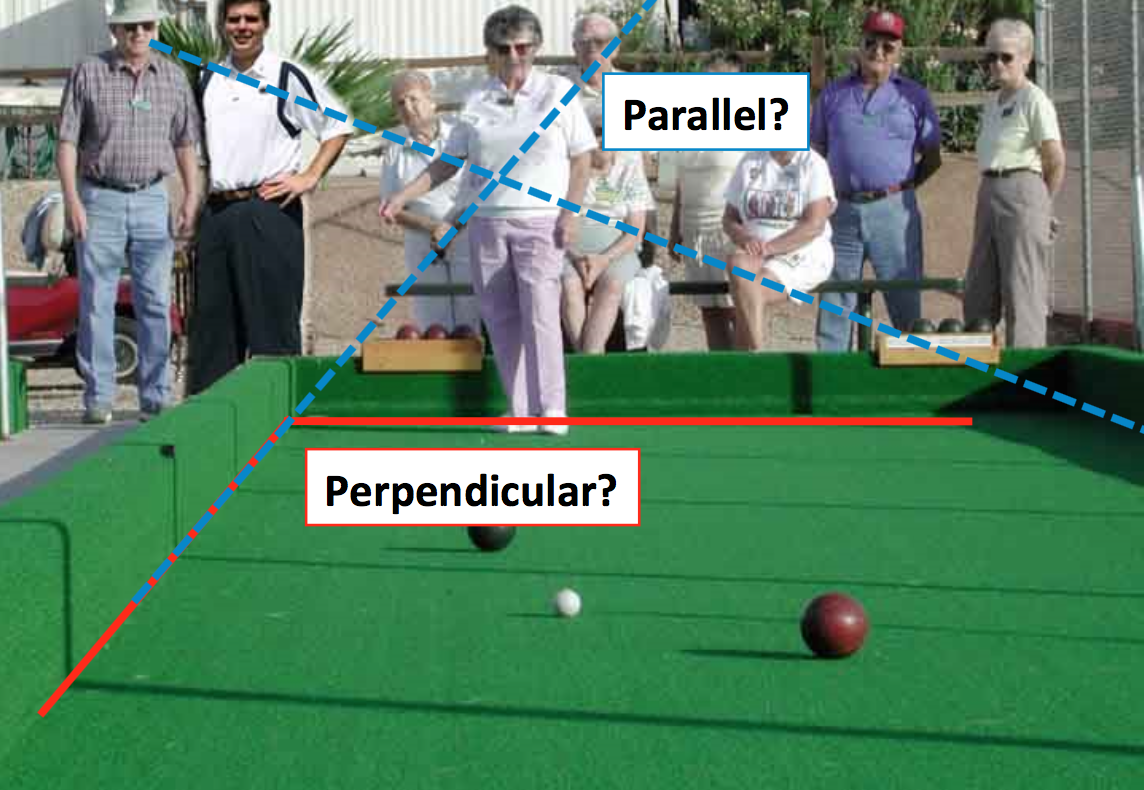
另一方面,虽然3D世界中的平行线在投影变换后相交(我们将交点称为Vanishing point),但是3D世界中互相平行的线,在2D平面上的Vanishing point为同一点。而所有平行线的Vanishing point又在同一条直线上。如下图所示(竖直的绿色平行线在投影变换后仍然保持平行,实际上并不想交,但我们这里认为其交于无穷远的某点)。
针孔相机模型
如下图所示,为针孔相机成像原理示意图。外部世界的一点$P$发出(或反射)的光线,经过小孔$O$,成像在在像平面$\Pi^\prime$的点$P^\prime$处。通过简单的相似三角形知识,可以得到图上的关系式。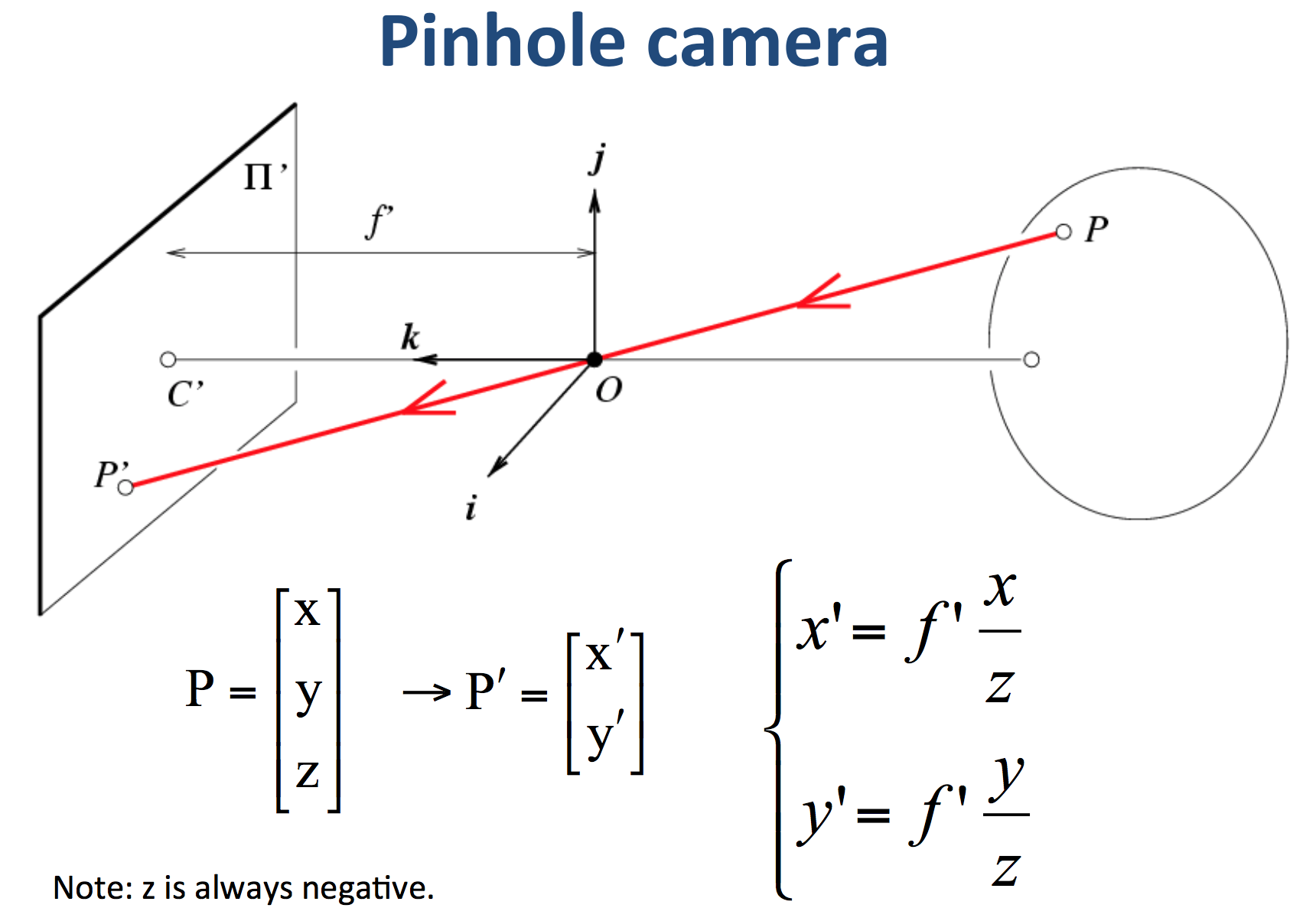
由上图可以知道,3D空间的一点$P$与成像平面上的对应点$P^\prime$坐标之间的数量关系为:
可是,由于变量$z$位于分母的位置,也就是说如果直接写成变换矩阵的话,这个矩阵是和变量$z$有关的,我们不想这样,而是想得到一个完全由相机本身确定的变换矩阵。所以,我们借鉴齐次矩阵的思想,将原来的点增加一个维度,转换为齐次坐标。如下图的两个例子所示。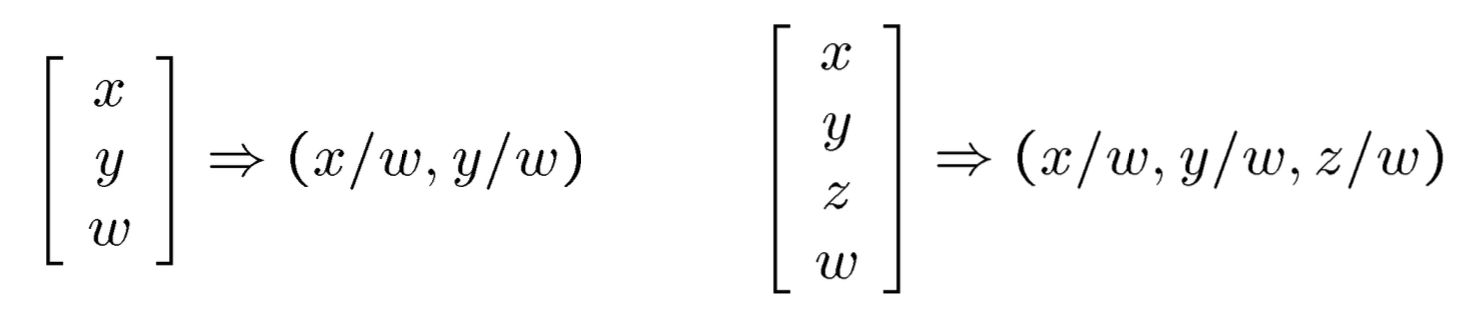
这样,我们可以将3D和2D之间的变换写成下面的形式。当实际计算的时候,我们首先将3D点转换为4维向量(在末尾补1),然后左乘变换矩阵。最后将得到的结果化为末尾元素为1的形式,这样,前面两个元素就代表了变换后2D点的坐标。这样做,使得变换矩阵$M$完全由相机参数(即焦距$f$)决定。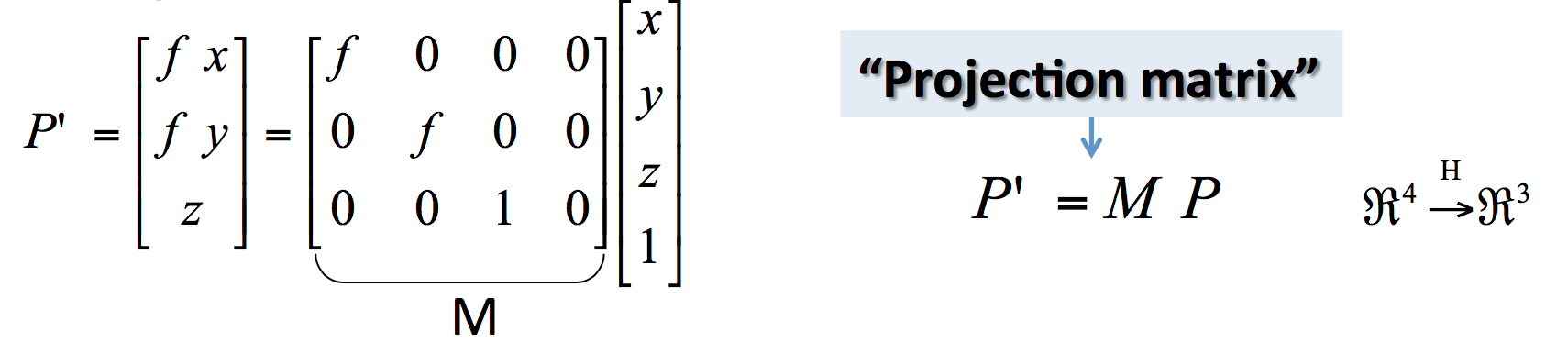
上面的式子只是理想情况下的相机模型,成立的假设条件较强,主要有以下几点假设:
- 内假设(和相机本身有关)
- 不同方向上焦距相同;
- 光学中心在相平面的坐标原点$(0, 0)$
- 没有倾斜(no skew)
- 外假设(和相机位姿有关,和相机本身参数无关)
- 相机没有旋转(坐标轴与世界坐标系方向重合)
- 相机没有平移(相机中心与世界坐标系中心重合)
其中,no skew情形我也不知道中文应该如何翻译。这种情况如图所示,由于剪切变形,成像平面的坐标轴并不是严格正交,使得两个轴之间实际存在一个很小的夹角。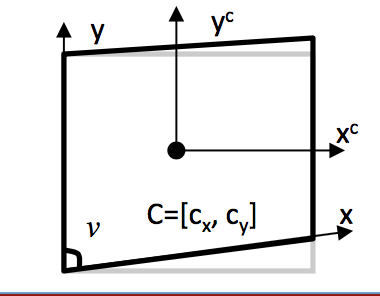
下面,按照slide的顺序逐渐将上述假设移去,分析变换矩阵$M$应该如何修正。
理想情况
理想情况以上假设全部满足,矩阵$M$如下所示。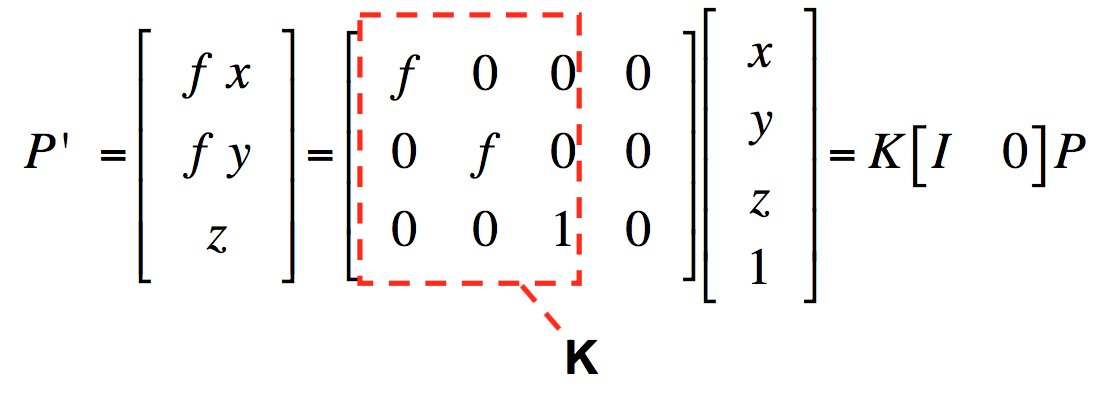
光学中心不在像平面的坐标原点
假设光学中心位于像平面内坐标为$(u_0, v_0)$的位置。则需要在理想情况计算的坐标基础上加上这个偏移量。所以,矩阵$M$被修正为: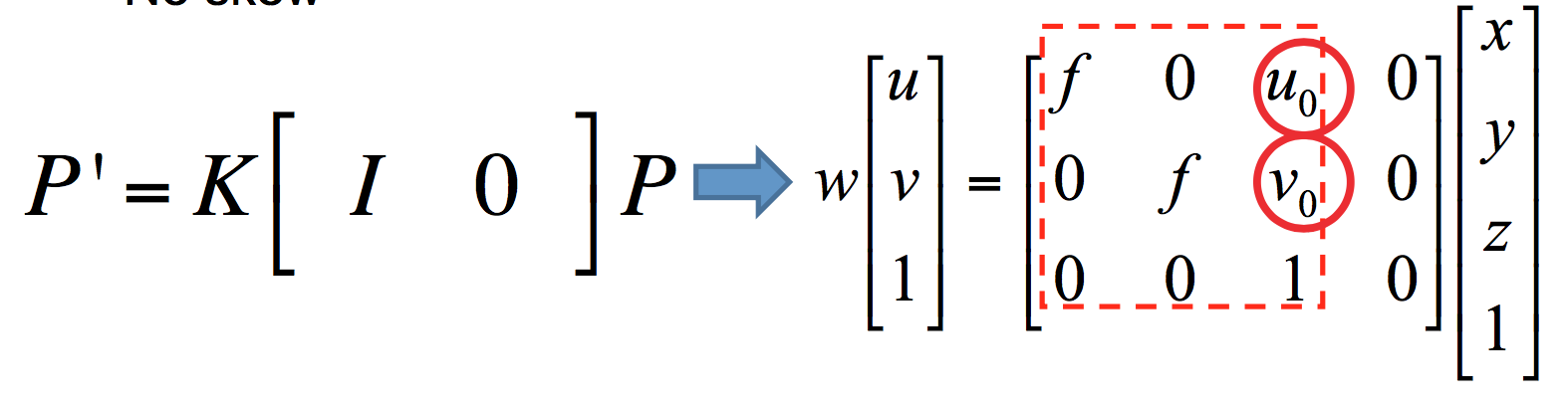
像素非正方形
由于透镜在$x$和$y$方向上的焦距不同,使得两个方向上的比例因子不同,不能再使用同一个$f$计算。修正如下: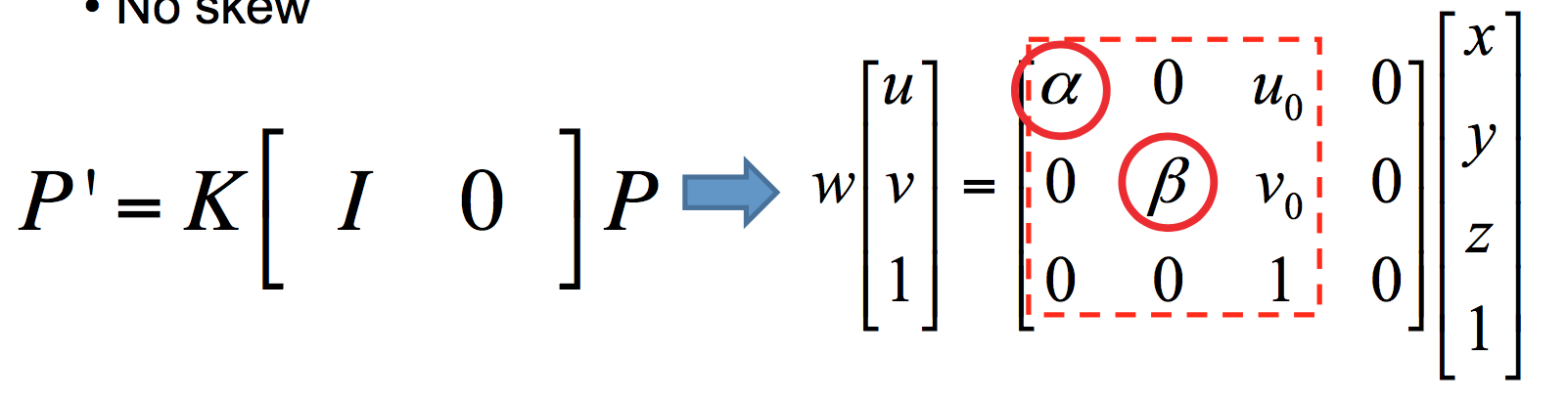
no skew
这时候$x$方向上其实有$y$轴坐标的分量,所以修正如下: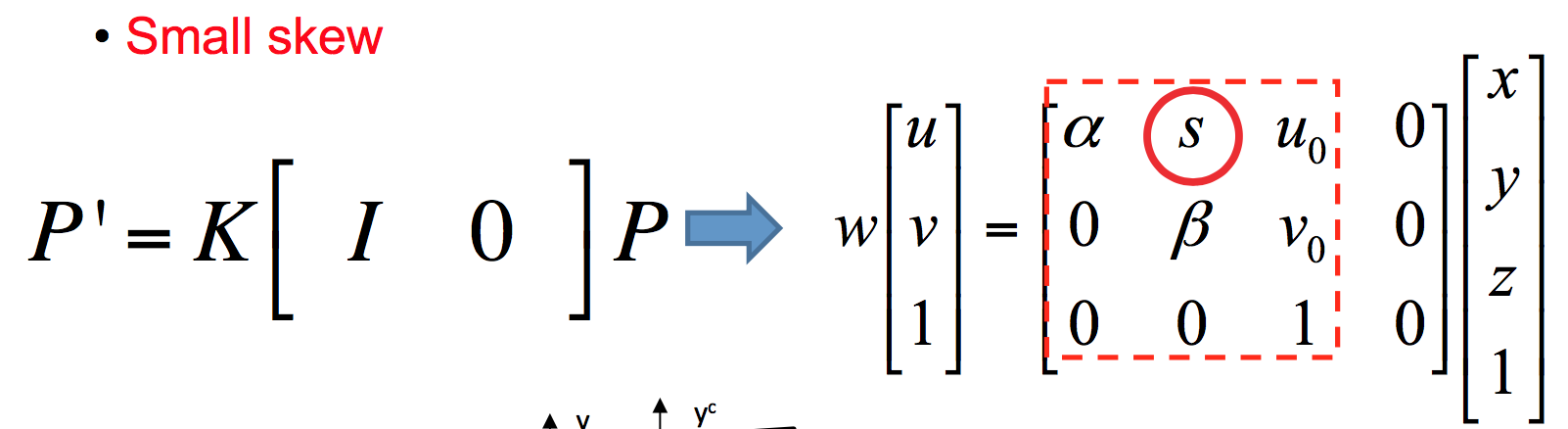
相机的旋转和平移
相机外部姿态很可能经过了旋转和平移,从而不与世界坐标系完全重合。如图所示。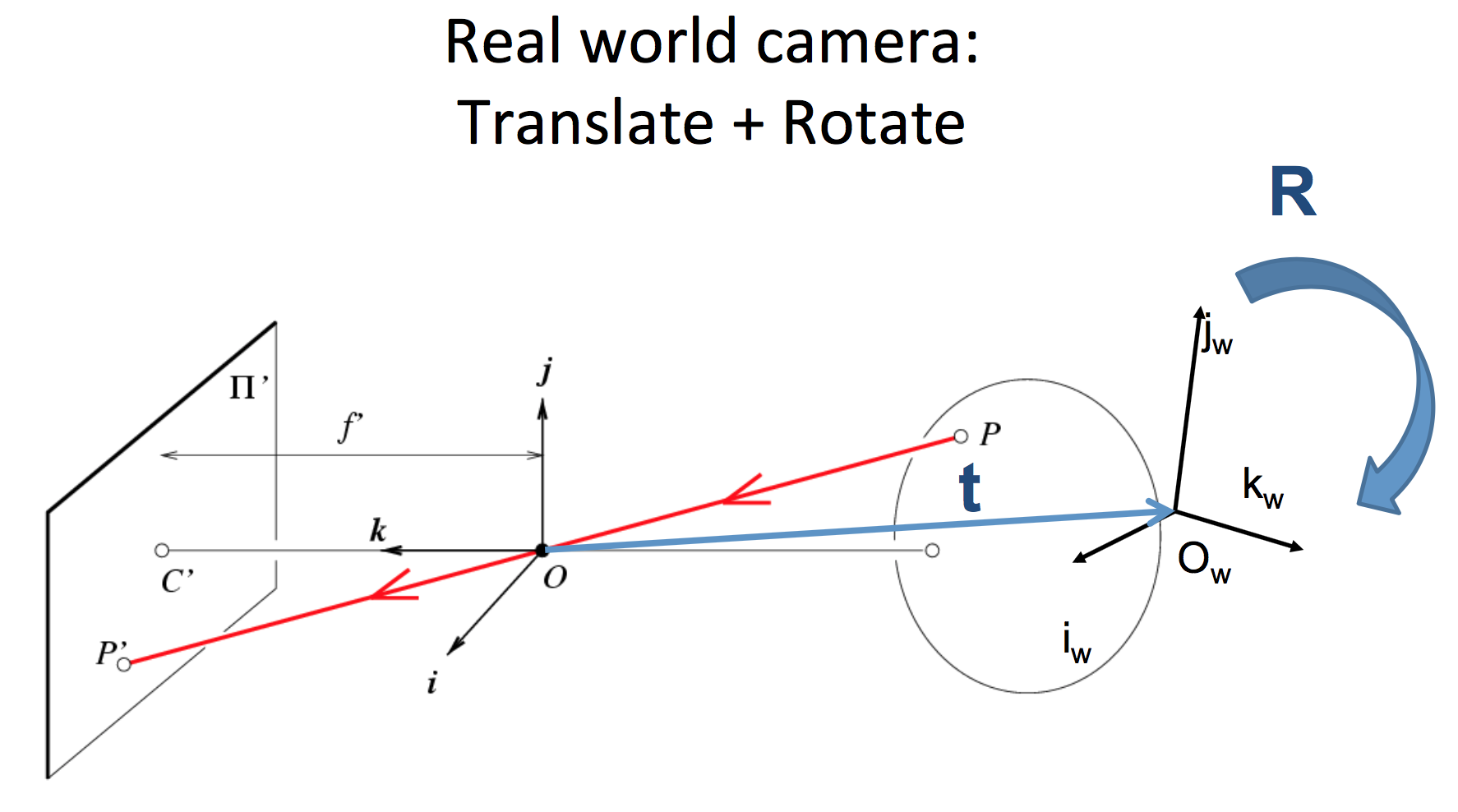
所以我们需要先对世界坐标系内的3D点做一个齐次变换,将其变换为一个中间坐标系,这个中间坐标系和相机坐标系是重合的。也就是我们的变换矩阵应该是下面这个形式的,其中,$H$是表征旋转和平移的齐次矩阵,$H\in \mathbb{R}^{3\times 4}$。
首先考虑较为简单的平移。所做的修正如下所示,也就是将原来的$\mathbb{0}$矩阵变为了一个平移向量。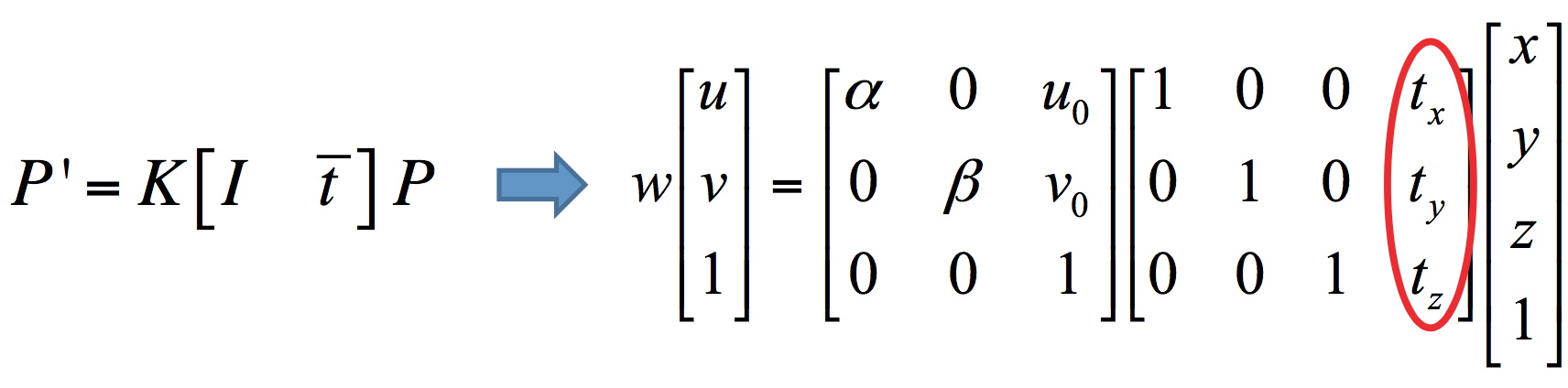
进一步考虑旋转时,我们将旋转分解为绕三个坐标轴的三次旋转,单次旋转矩阵如下所示: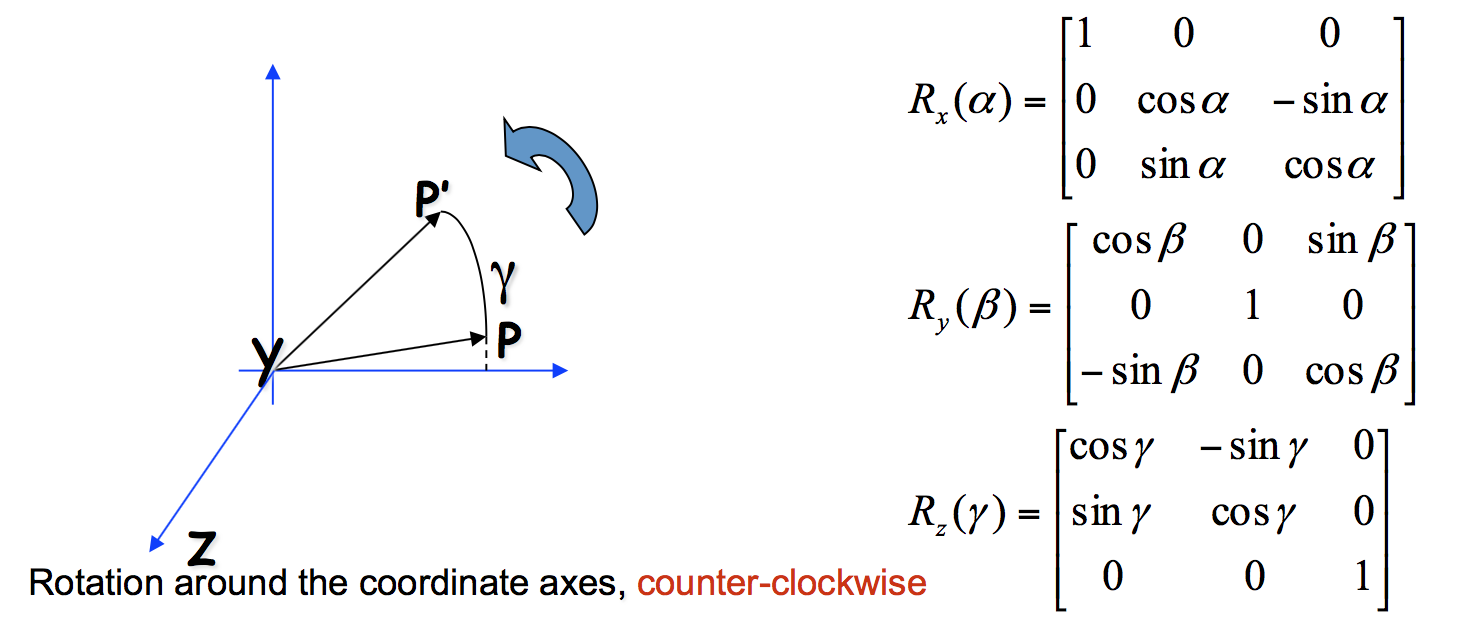
将它们按照旋转顺序左乘起来,可以得到修正后的变换形式如下: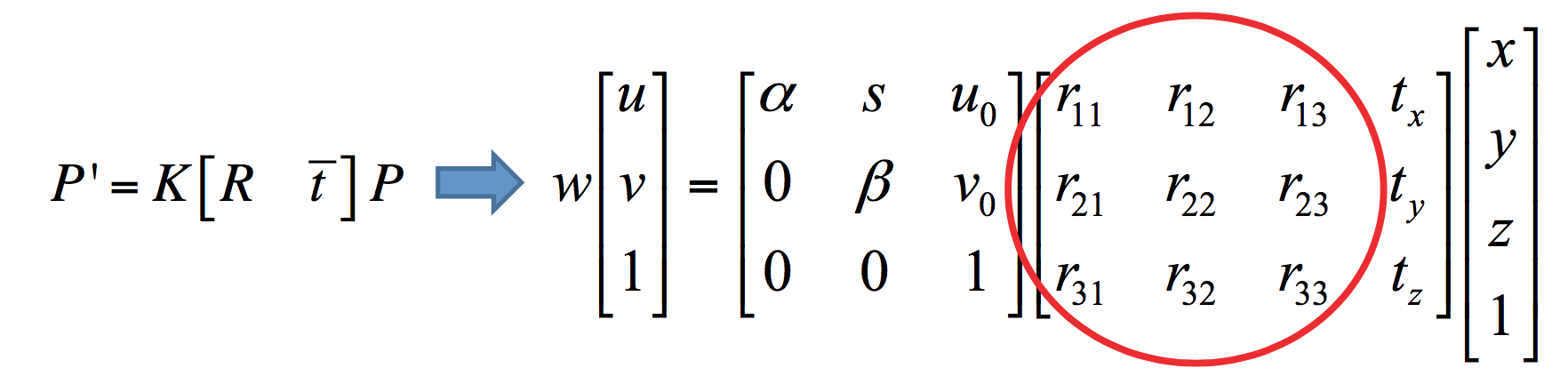
最终形式
综上所示,变换矩阵的最终形式为:
其中,内参数矩阵中有5个自由度,外参数矩阵中有6个自由度(3平移,3旋转)。
上面的内容总结起来,如下图所示。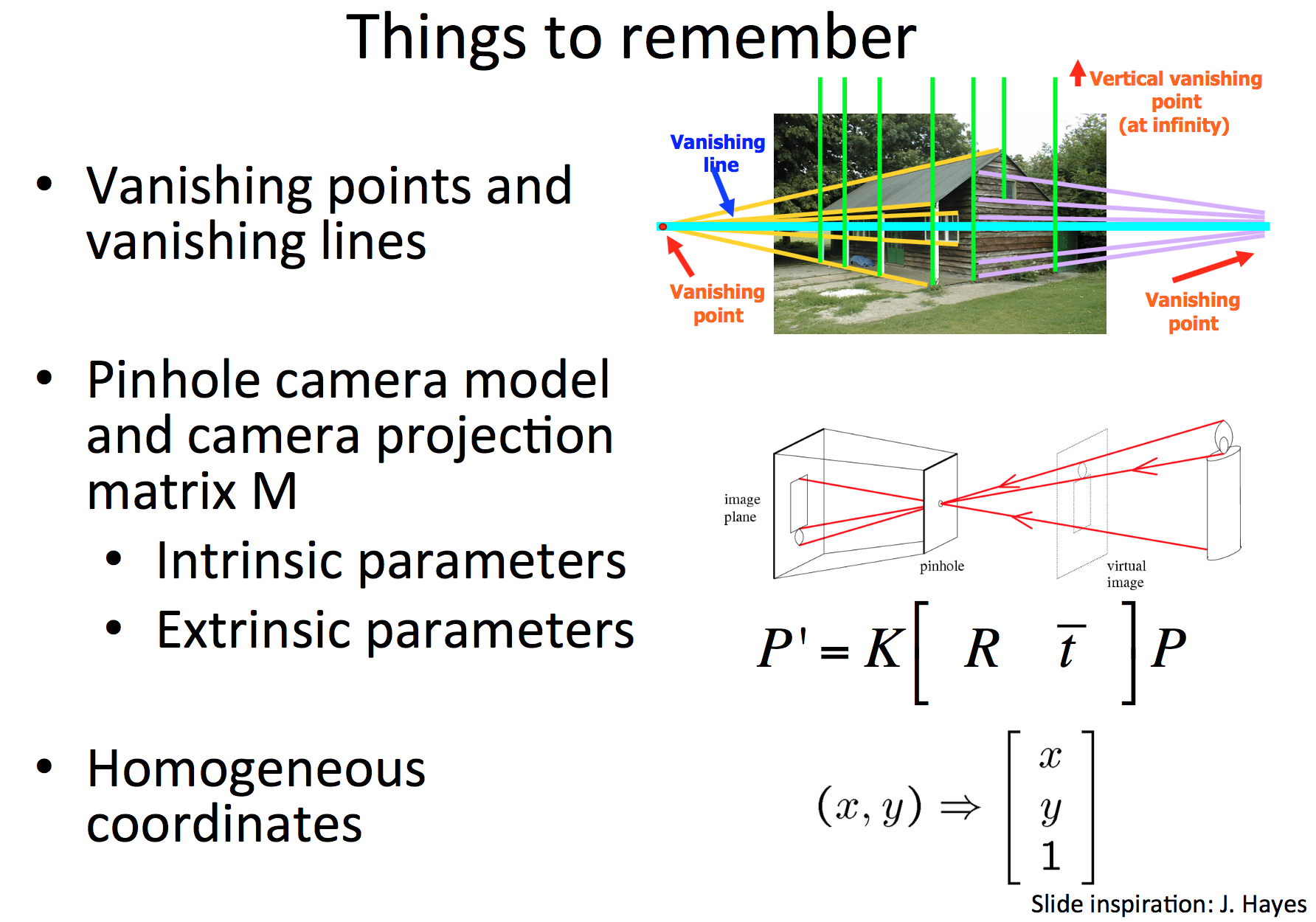
对极几何
基础概念
如下图所示,给出了对极几何中的几个基本概念。两个相机的中心分别位于$O$点和$O^{‘}$点,被观察物体位于$P$点。
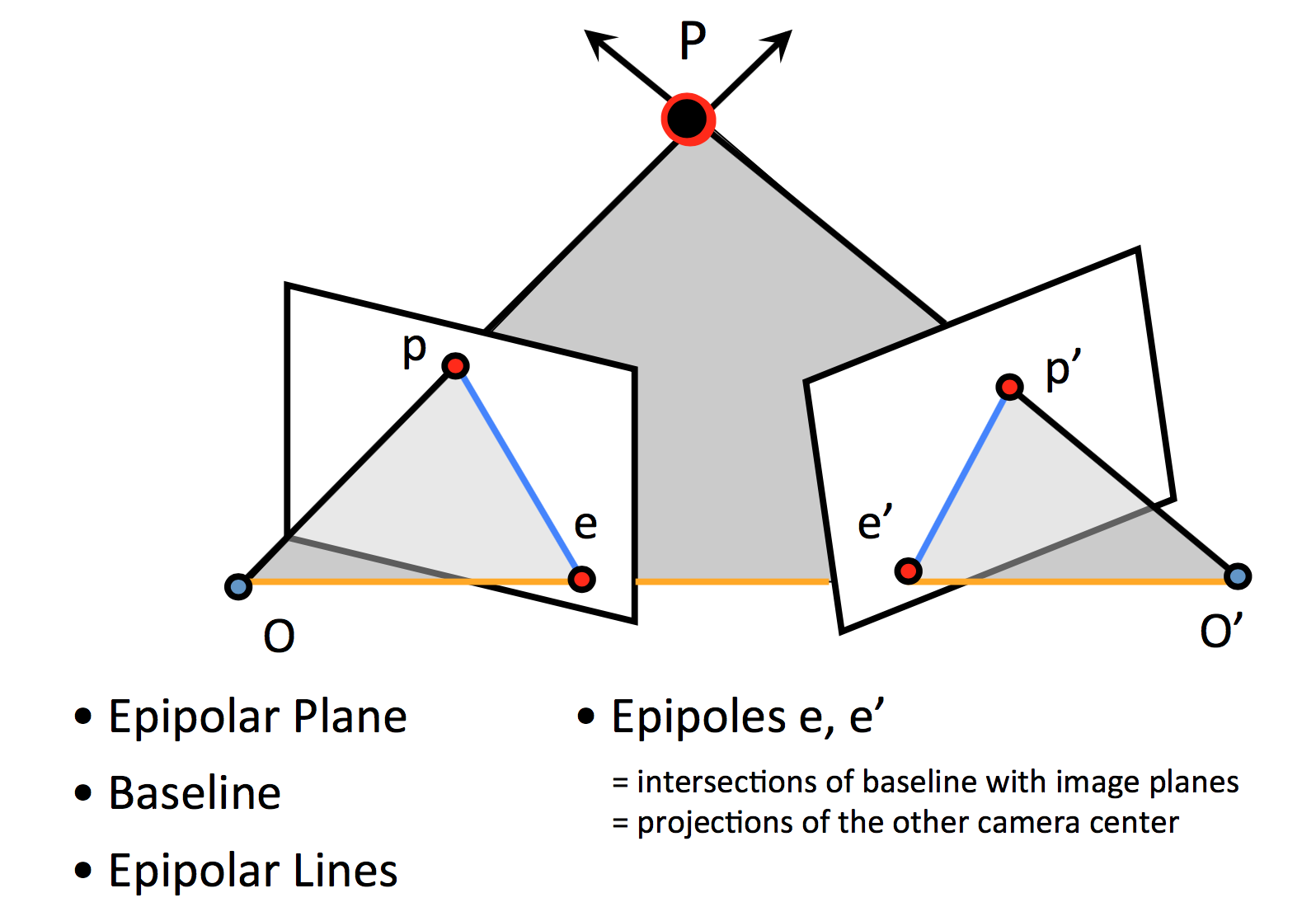
- 极点:$e$和$e^\prime$点分别是$OO^\prime$连线与两个成像平面的交点,也是相机中心在另一台相机成像平面上对应的像。
- 极平面:点$O$,$O^\prime$,$P$点共同确定的平面(灰色)
- 极线:极平面与两个成像平面的交线,即$pe$和$p^\prime e^\prime$(蓝色)
- 基线:两个相机中心的连线(黄色)
极线约束
从上图可以看出,如果两台相机已经给定,那么给定物体点在左边相机像平面内的成像点,则右边相机成像平面内的点被唯一确定。如何能够找到这个对应点呢?或者换种说法,在对极几何中,如何描述这种不同相机成像点的约束关系呢?
如下图所示,从上面的讨论我们已经知道,物点$P$在左右两个相机成像平面的坐标可以使用由相机内参数矩阵和外参数矩阵确定的齐次变换矩阵得到(下图在标注时,右侧相机的点应被标注为$p^\prime$)。为了简化问题,在下面的讨论时,我们假定相机都是理想的针孔相机模型,也就是说,变换矩阵只和外参数矩阵(也即是相机的位姿决定)。再做简化,认为世界坐标系与左侧相机的相机坐标系重合。那么,就得到了图上所示的变换矩阵$M$和$M^\prime$。其中,$R$是左右两个相机之间的旋转矩阵,$T$是$OO^\prime$有向线段,表明相机中心的位移。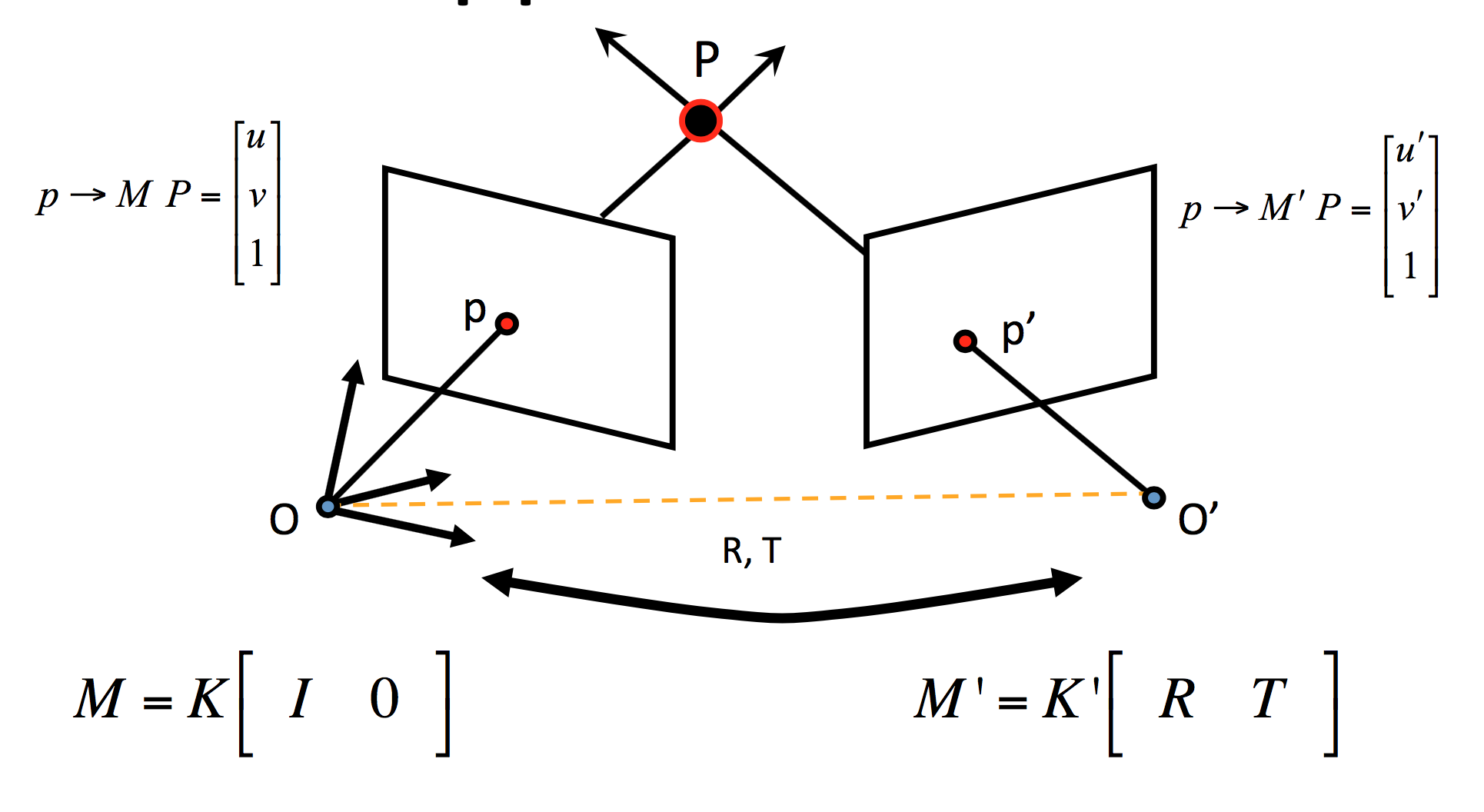
(下面的推导参考了博客:计算机视觉基础4——对极几何)。在下面的推导中,我们使用$p^\prime$表示在相机$O^\prime$下的向量$O\prime P$,符号$p$同理。那么,有如下关系成立:
$R(p-T) = p^\prime$