CS131-KMeans聚类

K-Means聚类是把n个点（可以是样本的一次观察或一个实例）划分到$k$个聚类中，使得每个点都属于离他最近的均值（此即聚类中心）对应的聚类，以之作为聚类的标准，满足最小化聚类中心和属于该中心的数据点之间的平方距离和（Sum of Square Distance，SSD）。

$$\text{SSD} = \sum_{i=1}^{k}\sum_{x\in c_i}(x-c_i)^2$$

目标函数

K-Means方法实际上需要确定两个参数，$c^\ast$和$\delta^\ast$。其中$c_{i}^\ast$代表各个聚类中心的位置，$\delta_{ij}^\ast$的取值为$\lbrace 0,1\rbrace$，代表点$x_j$是否被分到了第$i$个聚类中心。

那么，目标函数可以写成如下的形式。

$$c^\ast, \delta^\ast = \arg\min_{c,\delta} \frac{1}{N}\sum_{j=1}^{N}\sum_{i=1}^{k}\delta_{i,j}(c_i-x_j)^2$$

然而这样一来，造成了一种很尴尬的局面。一方面，要想优化$c_i$，需要我们给定每个点所属的类；另一方面，优化$\delta_{i,j}$，需要我们给定聚类中心。由于这两个优化变量之间是纠缠在一起的，K-Means算法如何能够达到收敛就变成了一个讨论“先有鸡还是先有蛋”的问题了。

实际使用中，K-Means的迭代过程，实际是EM算法的一个特例。

算法流程

K-Means算法的流程如下所示。

假设我们有$N$个样本点，$\lbrace x_1, \dots, x_N\rbrace, x_i\in\mathbb{R}^D$，并给出聚类数目$k$。

首先，随机选取一系列的聚类中心点$\mu_i, i = 1,\dots, k$。接着，我们按照距离最近的原则为每个数据点指定相应的聚类中心并计算新的数据点均值更新聚类中心。如此这般，直到收敛。

算法细节

初始化

上面的K-Means方法对初始值很敏感。朴素的初始化方法是直接在数据点中随机抽取$k$个作为聚类初始中心点。不够好的初始值可能造成收敛速度很慢或者聚类失败。下面介绍两种改进方法。

• kmeans++方法，尽可能地使初始聚类中心分散开（spread-out）。
  这种方法首先随机产生一个初始聚类中心点，然后按照概率$P = \omega(x-c_i)^2$选取其他的聚类中心点。其中$\omega$是归一化系数。

• 多次初始化，保留最好的结果。

K值的选取

在上面的讨论中，我们一直把$k$当做已经给定的参数。但是在实际操作中，聚类类别数通常都是未知的。如何确定超参数$k$呢？

我们可以使用不同的$k$值进行试验，并作出不同试验收敛后目标函数随$k$的变化。如下图所示，分别使用$1$到$4$之间的几个数字作为$k$值，曲线在$k=2$处有一个较为明显的弯曲点（elbow point）。故确定$k$取值为2。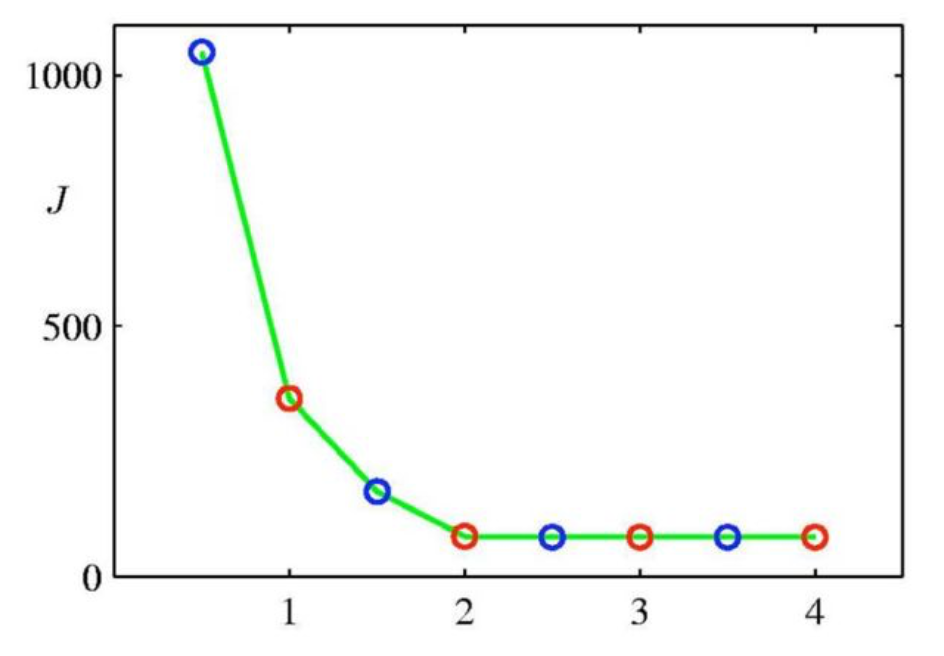

距离的度量

目标函数是各个cluster中的点与其中心点的距离均值。其中就涉及到了“距离”的量度。下面是几种较为常用的距离度量方法。

• 欧几里得距离（最为常用）
• 余弦距离（向量的夹角）
• 核函数（Kernel K-Means）

迭代终止条件

当判断算法已经收敛时，退出迭代。常用的迭代终止条件如下：

• 达到了预先给定的最大迭代次数
• 在将数据点assign到不同聚类中心时，和上轮结果没有变化（说明已经收敛）
• 目标函数（平均的距离）下降小于阈值

基于K-Means的图像分割

图像分割中可以使用K-Means算法。我们首先将一副图像转换为特征空间（Feature Space）。例如使用灰度或者RGB的值作为特征向量，就得到了1D或者3D的特征空间。之后，可以基于Feature Space上各点的相似度，将它们聚类。这样，就完成了对原始图像的分割操作。如下所示。

然而，上述方法有一个缺点。那就是在真实图像中，属于同一个物体的像素点常常在空间上是相关的（Spatial Coherent）。而上述方法没有考虑到这一点。我们可以根据颜色亮度和空间上的距离构建Feature Space，获得更加合理的分割效果。

在2012年PAMI上有一篇文章SLIC Superpixels Compared to State-of-the-art Superpixel Methods介绍了使用K-Means进行超像素分割的相关内容，可以参考。这里不再赘述了。

优点和不足

作为非监督学习中的经典算法，K-Means的一大优点便是实现简单，速度较快，最小化条件方差（conditional variance，good represention of data，这里没有具体解释，不太懂）。

它的缺点主要有：

• 对outlier比较敏感。如下图所示。由于outlier的存在，右边的cluster硬是被拉长了。这方面，K-Medians更有鲁棒性。
  
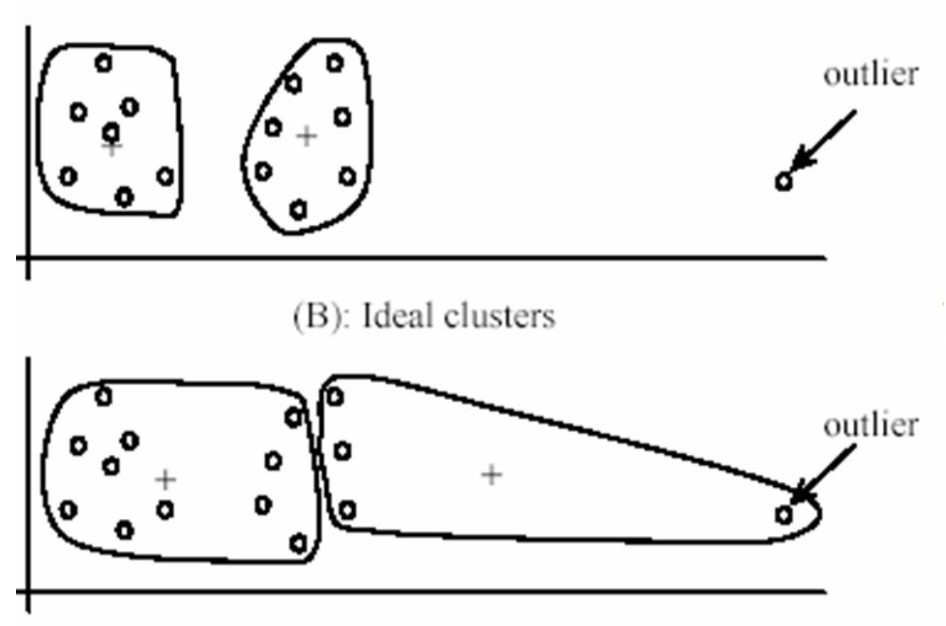
• 每个点只能确定地属于或不属于某一个cluster。可以参考高斯混合模型和Fuzzy K-Means的soft assignment。
• 在round shape情况下性能比较好（想想圆形和方形各点的欧几里得距离）。而且每个cluster最好数据点数目和分布的密度相近。
• 如果数据点有非凸形状分布，算法表现糟糕。可以参考谱聚类（Spectral Clustering）或者kernel K-Means。

针对K-Means，也有不少相关改进工作，参考下面这幅图吧。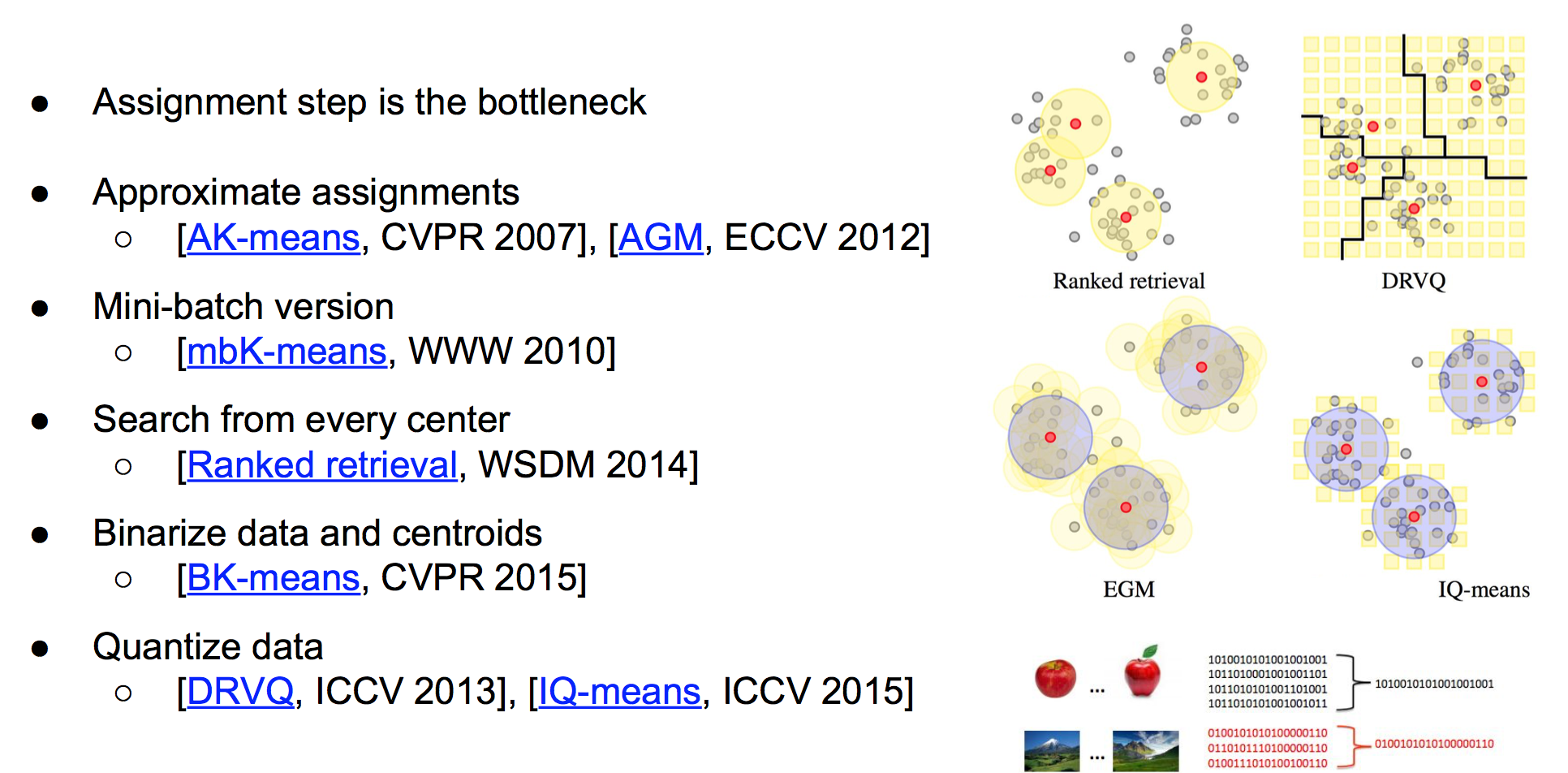

MATLAB实验

下面是我自己写的简单的K-Means demo。首先，在数据产生环节，确定$K = 3$个cluster的中心位置，并随机产生$N$个数据点，并使用scatter函数做出散点图。

代码中的主要部分为my_kmeans函数的实现（为了不与内建的kmeans函数重名，故加上了my前缀）。在此函数内部，首先随机产生$K$个聚类中心，并对数据点进行初始的指定。接着，在迭代过程中，不断计算均值来更新聚类中心和assignment，当达到最大迭代次数或者相邻两次迭代中assignment的值不再变化为止，并计算对应的目标函数$J$的值。

注意到该函数初始确定聚类中心时有一段注释的代码，该段代码用于debug时，指定聚类中心，去除随机性，以验证后续K-Means迭代的正确性。

%% generate data
K = 3;   % number of clusters
pos = [-5, 5; 0, 1; 3, 6];  % position of cluster centers
N = 20;    % number of data points
R = 3;     % radius of clusters
data = zeros(N, 2);    % data
class = zeros(N, 1);   % index of cluster

for i = 1:N
    idx = randi(3, 1);
    dr = R*rand();
    data(i, :) = pos(idx, :) + [dr*cos(rand()*2*pi), dr*sin(rand()*2*pi)];
    class(i) = idx;
end

%% visualization data points
figure
hold on
color = [1,0,0; 0,1,0; 0,0,1];
for i = 1:K
    x = data(class == i, 1);
    y = data(class == i, 2);
    scatter(x, y, 150, repmat(color(i,:), [length(x), 1]), 'filled');
end

%% K-Means
best_J = 1E100;
best_idx = 0;
for times = 1:5  % 5 times experiments to choose the best result
    [mu, assignment, J] = my_kmeans(data, K);
    if best_J > J
        best_idx = times;
        best_J = J;
    end
    fprintf('%d experiment: J = %f\n', times, J);
    disp(mu);
end
fprintf('best: %d experiment: J = %f\n', best_idx, best_J);

%% basic functions
function J = ssd(X, mu, assignment)
% sum of square distance
% X -- data, N*D matrix
% mu -- centers of clusters, K*D matrix
% assignment -- current assignment of data to clusters
J = 0;
K = size(mu, 1);
for k = 1:K
    x_k = X(assignment == k, :);
    mu_k = mu(k, :);
    err2 = bsxfun(@minus, x_k, mu_k).^2;
    J = J + sum(err2(:));
end
J = J / size(X, 1);
end

function mu = compute_mu(X, assignment, K)
mu = zeros(K, size(X, 2));
for k = 1:K
    x_k = X(assignment == k, :);
    mu(k, :) = mean(x_k, 1);
end
end

function assignment = assign(X, mu)
% assign data points to clusters
N = size(X, 1);
assignment = zeros(N, 1);
for i = 1:N
    x = X(i, :);
    err2 = bsxfun(@minus, x, mu).^2;
    dis = sum(err2, 2);
    [~, idx] = min(dis);
    assignment(i) = idx;
end
end

function [mu, assignment, J] = my_kmeans(X, K)
N = size(X, 1);
assignment = zeros(N, 1);
idx = randsample(N, K);
mu = X(idx, :);

% for i = 1:K
%     for j = 1:N
%         if assignment_gt(j) == i
%             mu(i,:) = X(j,:);
%             break;
%         end
%     end
% end
figure
hold on
color = [1,0,0; 0,1,0; 0,0,1];
scatter(mu(:,1), mu(:,2), 200, color, 'd');
for iter = 1:20
    assignment_prev = assignment;
    assignment = assign(X, mu);
    if assignment == assignment_prev
        break;
    end
    mu_prev = mu;
    mu = compute_mu(X, assignment, K);
    scatter(mu(:, 1), mu(:, 2), 200, color, 'd');
    MU = zeros(2*K, 2);
    MU(1:2:end, :) = mu_prev;
    MU(2:2:end, :) = mu;
    mu_x = reshape(MU(:, 1), [], K);
    mu_y = reshape(MU(:, 2), [], K);
    plot(mu_x, mu_y, 'k-.');

end
for i = 1:K
    x = X(assignment == i, 1);
    y = X(assignment == i, 2);
    scatter(x, y, 150, repmat(color(i,:), [length(x), 1]), 'filled');
end
J = ssd(X, mu, assignment);
end

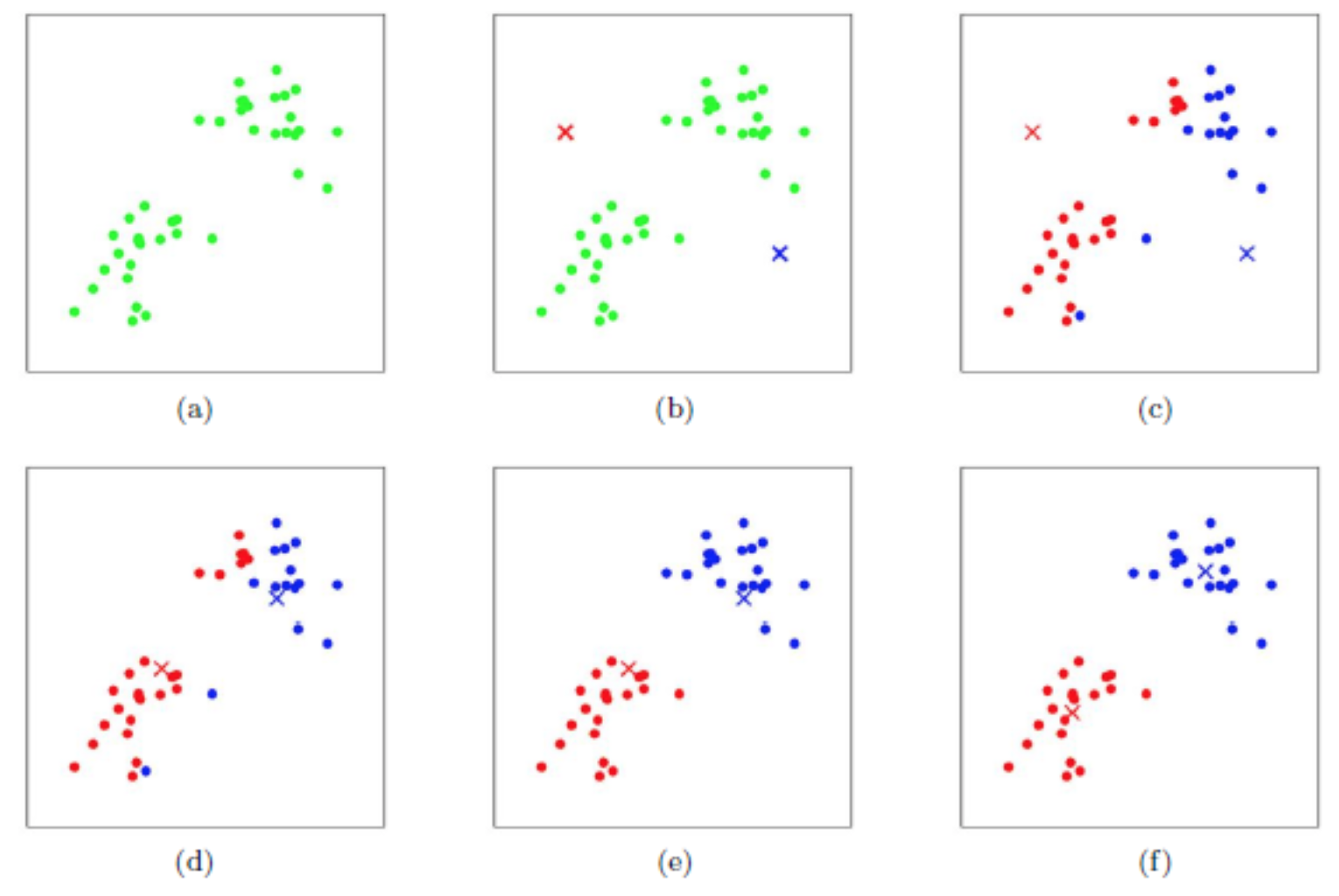
在demo中，随机选取初始化的聚类中心，重复进行$5$次实验。下图是产生的原始数据的散点图。用不同的颜色标明了cluster。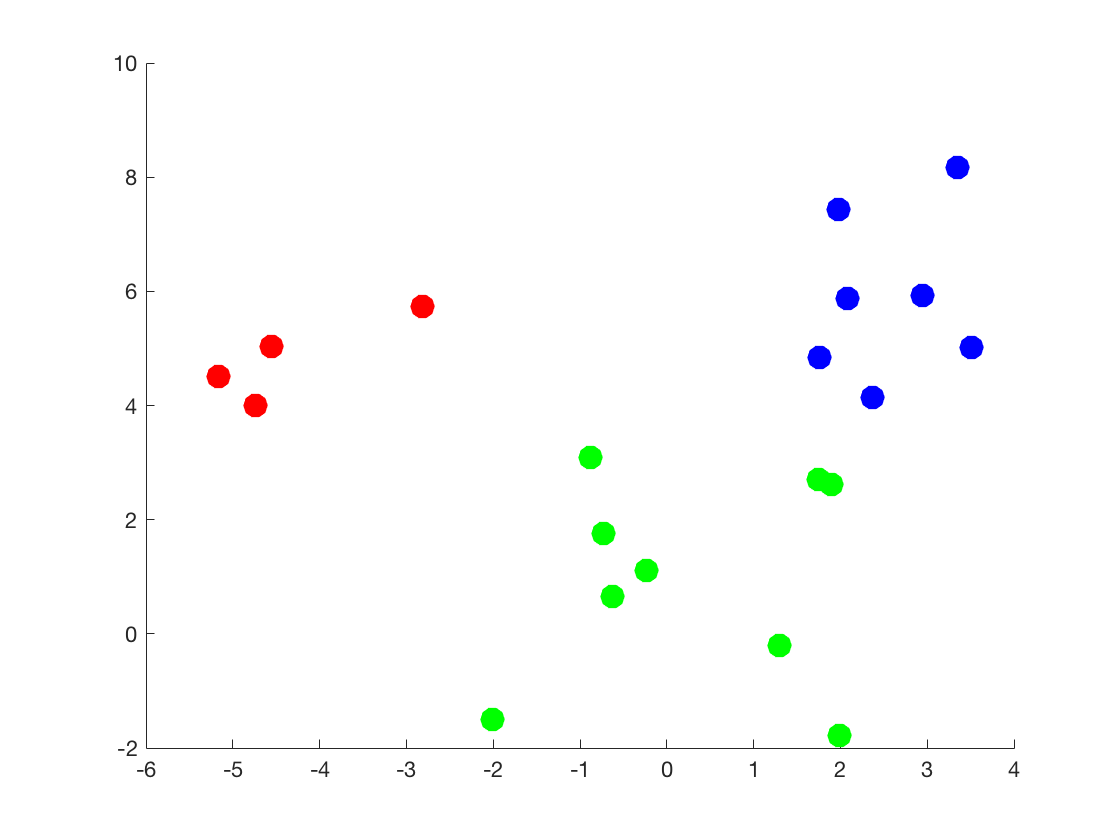

下图是某次的实验结果，其中菱形和它们之间的连线指示了聚类中心的变化。注意，颜色只是用来区别不同的cluster，和上图并没有对应关系。可以看到，初始化时绿色标注的cluster的中心（也即是上图中的红色cluster）虽然偏离了很远，但是在迭代过程中也能实现纠正。

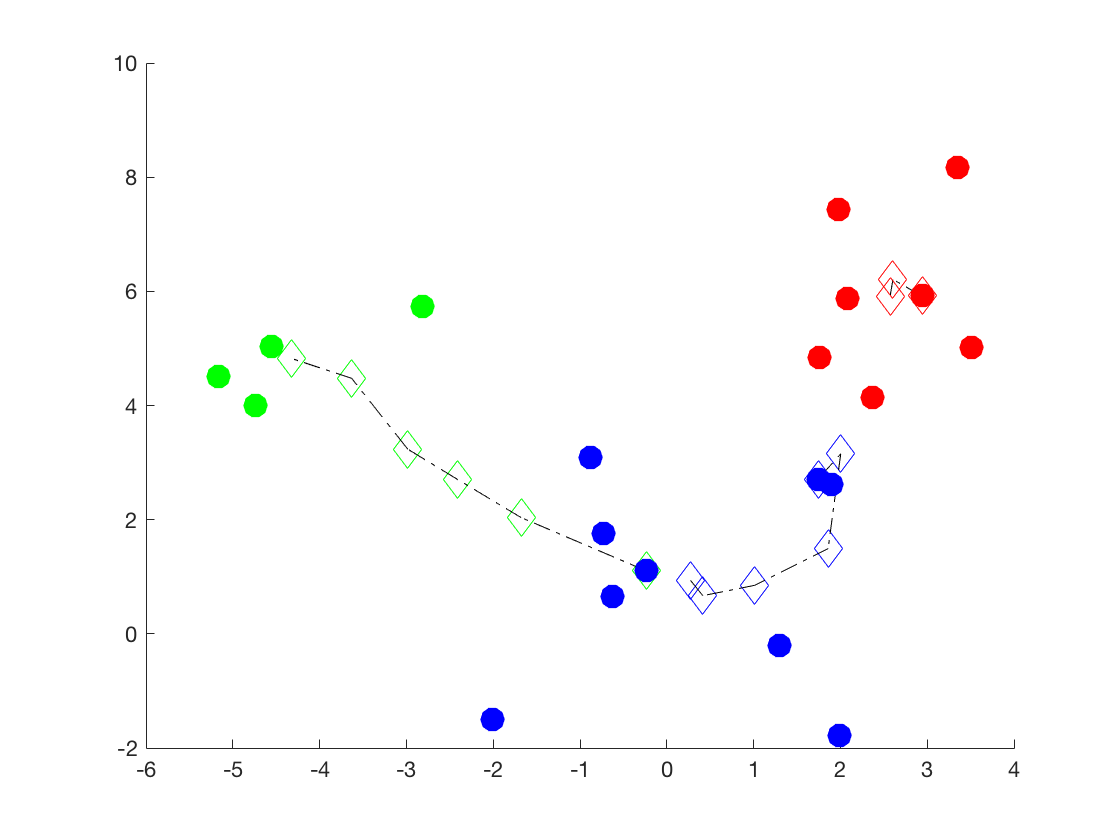
再换个大点的数据集来做，效果貌似还不错~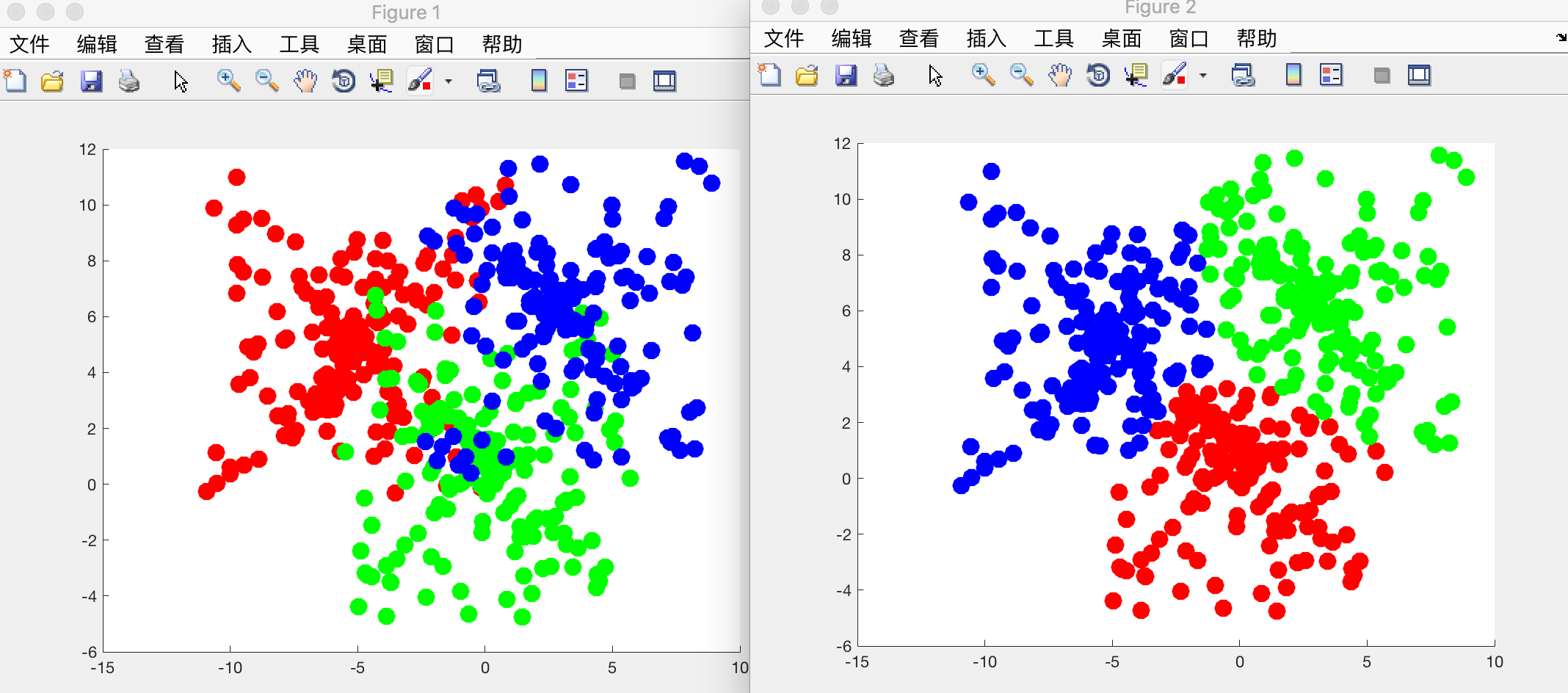

PS

这里插一句与本文内容完全无关的一个tip：在Markdown中使用LaTex时，如果在内联形式（也就是行内使用两个美元符号插入公式）时，如果有多个下划线，那么Markdown有时会将下划线之间的部分认为是自己的斜体标记，如下所示：

$c_{i}^\ast$ XXX $\delta_{ij}^\ast$

它的显示效果为$c{i}^\ast$ XXX $\delta{ij}^\ast$。

这时候，只需在下划线前加入反斜线进行转义即可（虽然略显麻烦）。如下所示：

$c\_{i}^\ast$ XXX $\delta\_{ij}^\ast$

它的显示效果为$c_{i}^\ast$ XXX $\delta_{ij}^\ast$。

具体分析可以参见博客。