Silver RL课程 - MDP

Silver在英国UCL讲授强化学习的slide总结。背景介绍部分略去不表，第一篇首先介绍强化学习中重要的数学基础-马尔科夫决策过程（MDP）。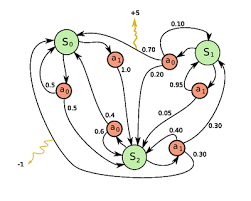

马尔科夫性质

不严谨地来说，马尔科夫性质是指未来与过去无关，只与当前的状态有关。我们说某个State是Markov的，等价于下面的等式成立：

$$P[S_{t+1}|S_t] = P[S_{t+1}|S_1, \dots, S_t]$$

定义状态转移概率（State Transition Probability）如下：

$$P_{ss^\prime} = P[S_{t+1}=s^\prime|S_t=s]$$

前后两个时刻的状态不同取值的状态转移概率可以写成一个矩阵的形式。矩阵中的任意元素$P_{i,j}$表示$t$时刻状态$i$在$t+1$时刻转移到状态$j$的概率。矩阵满足行和为$1$的约束。

下面，我们从马尔科夫性质展开，逐步地加入一些额外的参量，一步步引出强化学习中的马尔科夫决策过程。

马尔科夫过程

马尔科夫过程（或者叫做马尔科夫链）是指随机过程中的状态满足马尔科夫性质。我们可以使用二元组$(S, P)$来描述马氏过程。其中，

• $S$是一个有限状态集合。
• $P$是状态转移矩阵，定义如上。

马尔科夫奖赏过程

马尔科夫奖赏过程（不知道如何翻译，Markov reward process）在马氏过程基础上加上了状态转移过程中的奖赏reward。可以使用四元组$(S, P, R, \gamma)$来表示。其中，

• $R$代表奖励函数，$R_s = E[R_{t+1}|S_t=s]$，是指当前状态为$s$时，下一步状态转移过程中的期望奖励。
• $\gamma$是折旧率（discount），$\gamma \in [0,1]$

定义回报（Return）为当前时刻往后得到的折旧总奖励，即：

$$G_t = R_{t+1}+\gamma R_{t+2}+... = \sum_{k=0}^{\infty}\gamma^kR_{t+k+1}$$

折旧率的引入，有以下几点考虑：

• 在有环存在的马氏过程中，避免了无穷大回报的出现。
• 未来的不确定性对当前的影响较小。
• 事实上的考虑，例如投资市场上，即时的奖励比迟滞的奖励能够有更多的利息。
• 人类行为倾向于即时奖励。
• 如果马氏过程是存在终止的，有的时候也可以使用$\gamma=1$，也就是不打折。

值函数

值函数（Value function）的意义是以期望的形式（条件期望）给出了状态$s$的长期回报，如下：

$$v(s) = E[G_t|S_t=s]$$

值函数可以分为两个部分，即时奖励$R_{t+1}$和后续状态的折旧值函数。如下所示：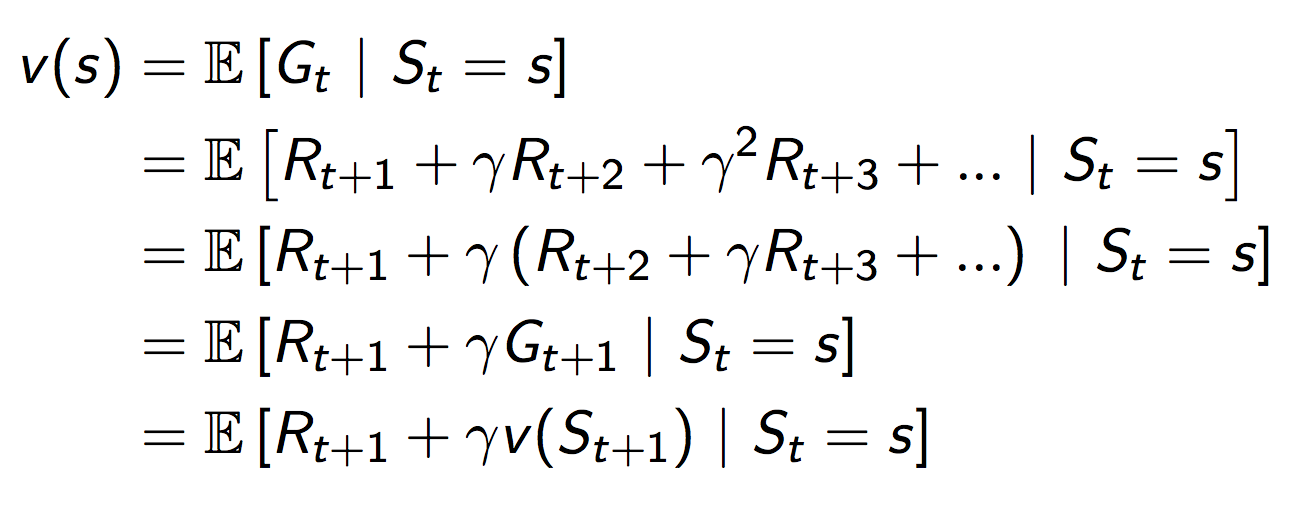

最后一步推导时，第二项的变形从直觉上推断还是比较容易的，但是还是把比较严格的推导过程写在下面：

$$\begin{aligned} E[G_{t+1}|S_t = s] &= \sum_{s^\prime\in S}E[G_{t+1}|S_{t+1}=s^\prime]P(S_{t+1}=s^\prime|S_t=s)\\ &=\sum_{s^\prime}v(S_{t+1}=s^\prime)P(S_{t+1}=s^\prime|S_t=s)\\ &=E[v(S_{t+1})|S_t=s] \end{aligned}$$

上面的结论就是贝尔曼方程，它给出了计算值函数的递归公式。如下图所示，状态节点$s$处的值函数可以分为两个部分，分别是转换到状态$s^\prime$过程中收到的奖励$r$，和从新的状态$s^\prime$出发，得到的值函数。我们想要知道$t$时刻某个状态$s$的值函数，只需要从后向前遍历，递归地去计算。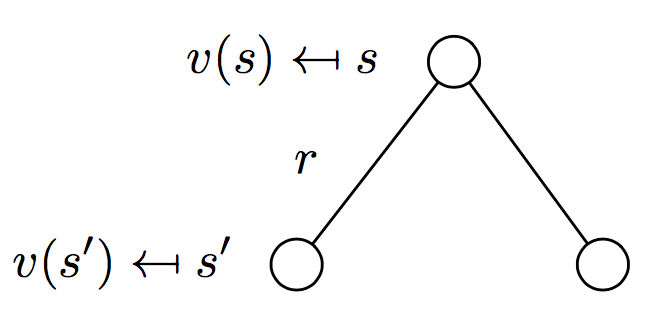

把上面形式求期望的过程展开，可以得到下面的等价形式（更像上面补充的证明过程的思路）。其中，后面一项就是状态转移构成的树结构中以当前状态节点$s$为父节点的所有子节点的值函数，用转移概率进行加权。这个比上式更为直观。

$$v(s) = R_s + \gamma\sum_{s^\prime \in S}P_{ss^\prime}v(s^\prime)$$

或者写成下面的矩阵形式，更加紧凑：

$$v = R+\gamma Pv$$

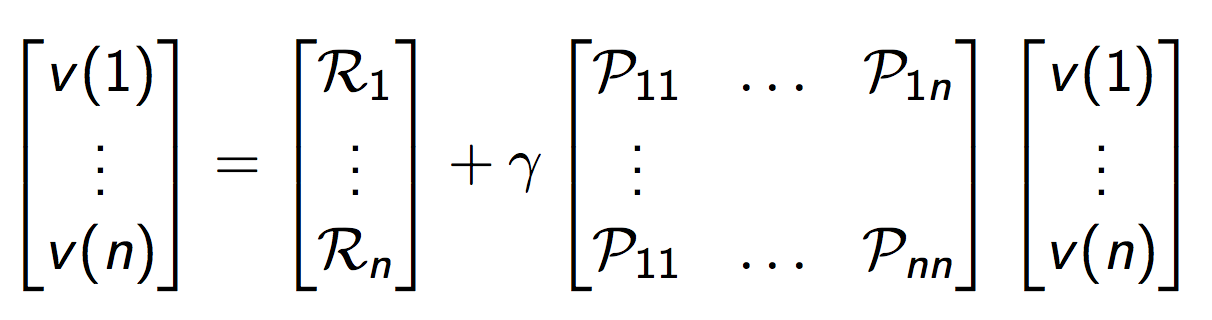
当我们对系统模型（包括奖励函数和概率转换矩阵）全部知道时，可以直接求解贝尔曼方程如下：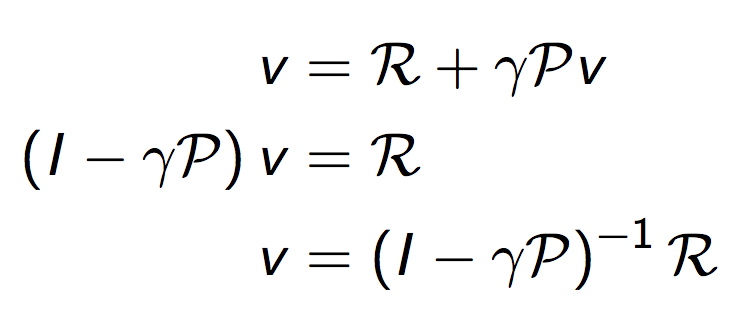

对于含有$n$个状态的系统，求解复杂度是$\mathcal{O}(n^3)$。当$n$较大时，常用的替代的迭代求解方法有：

• 动态规划 DP
• 蒙特卡洛仿真（Monte-Carlo evaluation）
• 时间差分学习（Temporal Difference Learning）

马尔科夫决策过程

马尔科夫决策过程（MDP）是带有决策的马尔科夫奖励过程。其中有一个env（环境），其状态量满足马尔科夫性质。MDP可以用五元组$(S,A,P,R,\gamma)$描述。其中，

• $A$是一个有限决策集合。
• $P_{ss^\prime}^a = P(S_{t+1}=s^\prime|S_t=s, A_t=a)$是状态转移概率矩阵。
• $R_{s}^a = E[R_{t+1}|S_t=s, A_t=a]$是奖励函数（与动作也挂钩）

策略

策略（Policy）$\pi$是指在给定状态情况下，采取动作的概率分布，如下：

$$\pi(a|s)=P(A_t=a|S_t=s)$$

对于一个智能体，如果策略确定了，那么它对环境的表现也就决定了。MDP的策略与历史无关，只与当前的状态有关。同时，策略是平稳过程，与时间无关。例如，无论在开局，还是终局，只要棋盘上的落子一样（也就是状态一样），那么围棋程序应该给出相同的落子动作决策。

当我们给定一个MDP和相应的策略$\pi$时，状态转移过程$S_1,S_2,\dots$是一个马氏过程$(S, P^\pi)$（上标$\pi$表示$P$由$\pi$决定）。而状态和奖励构成的过程$S_1,R_1,\dots$是一个马氏奖赏过程$(S, P^\pi, R^\pi, \gamma)$。具体来说，如下（就是全概率公式）：

$$\begin{aligned} P_{ss^\prime}^\pi &= \sum_{a\in A}\pi(a|s)P_{ss^\prime}^a\\ R_s^\pi &=\sum_{a\in A}\pi(a|s)R_s^a \end{aligned}$$

值函数

MDP的值函数$v_\pi(s)$是指在当前状态$s$出发，使用策略$\pi$得到的回报期望，即，

$$v_\pi(s) = E_\pi[G_t|S_t=s]$$

引入“动作-值”函数（action-value function）$q_\pi(s,a)$，意义是从当前状态$s$出发，执行动作$a$，再使用策略$\pi$得到的回报期望，即，

$$q_\pi(s,a) = E_\pi[G_t|S_t=s,A_t=a]$$

贝尔曼方程

两者的关系如下如所示（通过全概率公式联系）：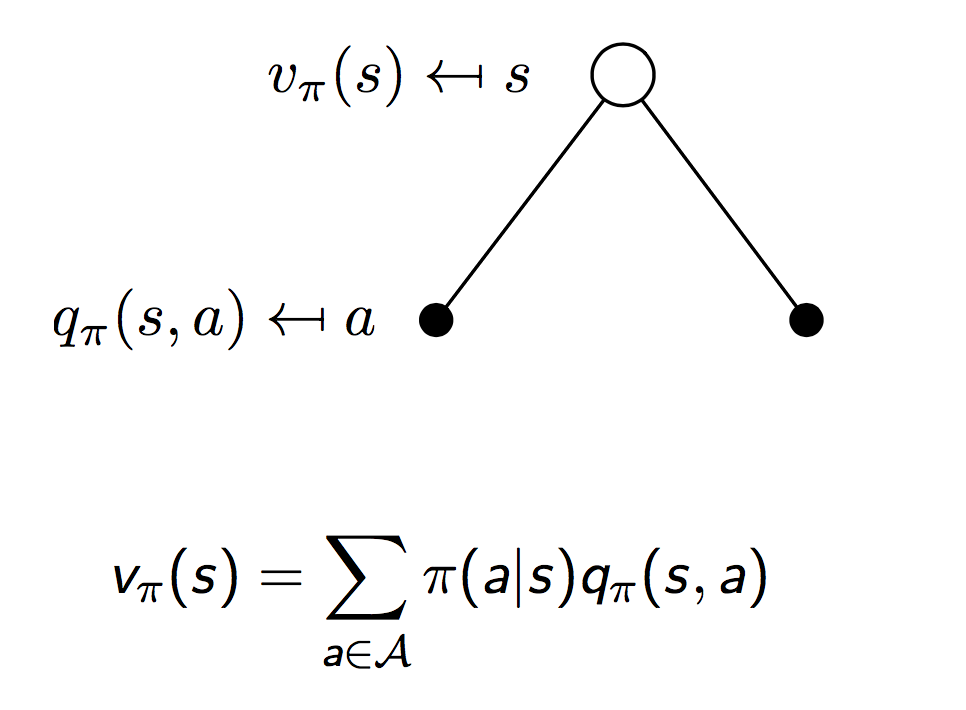

注意上图描述的是$t$时刻的状态$s$下，$v(s)$和$q(s,a)$的关系。我们继续顺着状态链往前，可以得到下图所示$q(s,a)$和$t+1$时刻的状态$s^\prime$的值函数$v(s^\prime)$之间的关系。同样是一个全概率公式：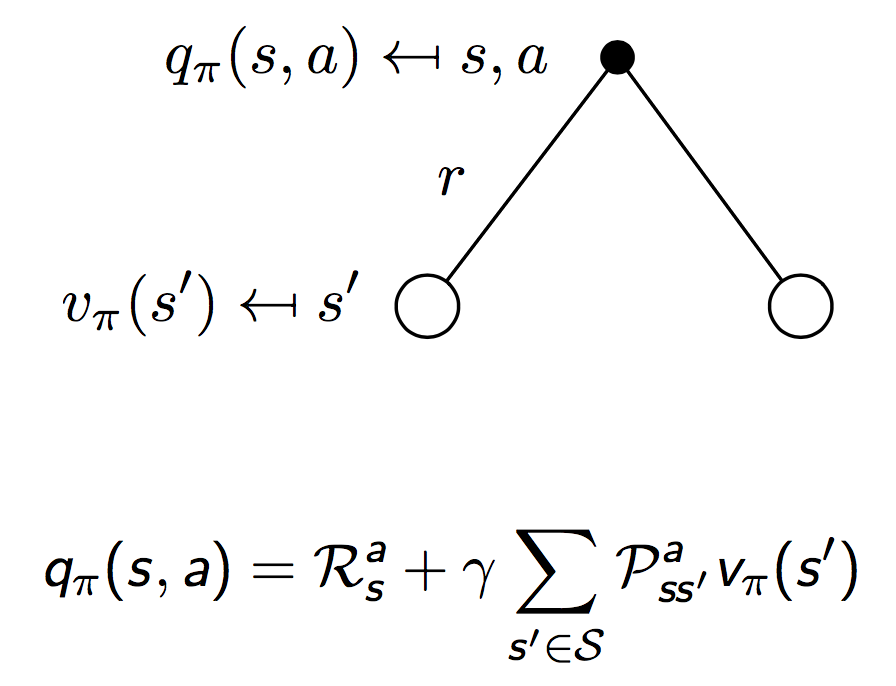

综合上面两幅图中给出的关系，我们有相邻时刻值函数$v(s)$和$v(s^\prime)$的关系：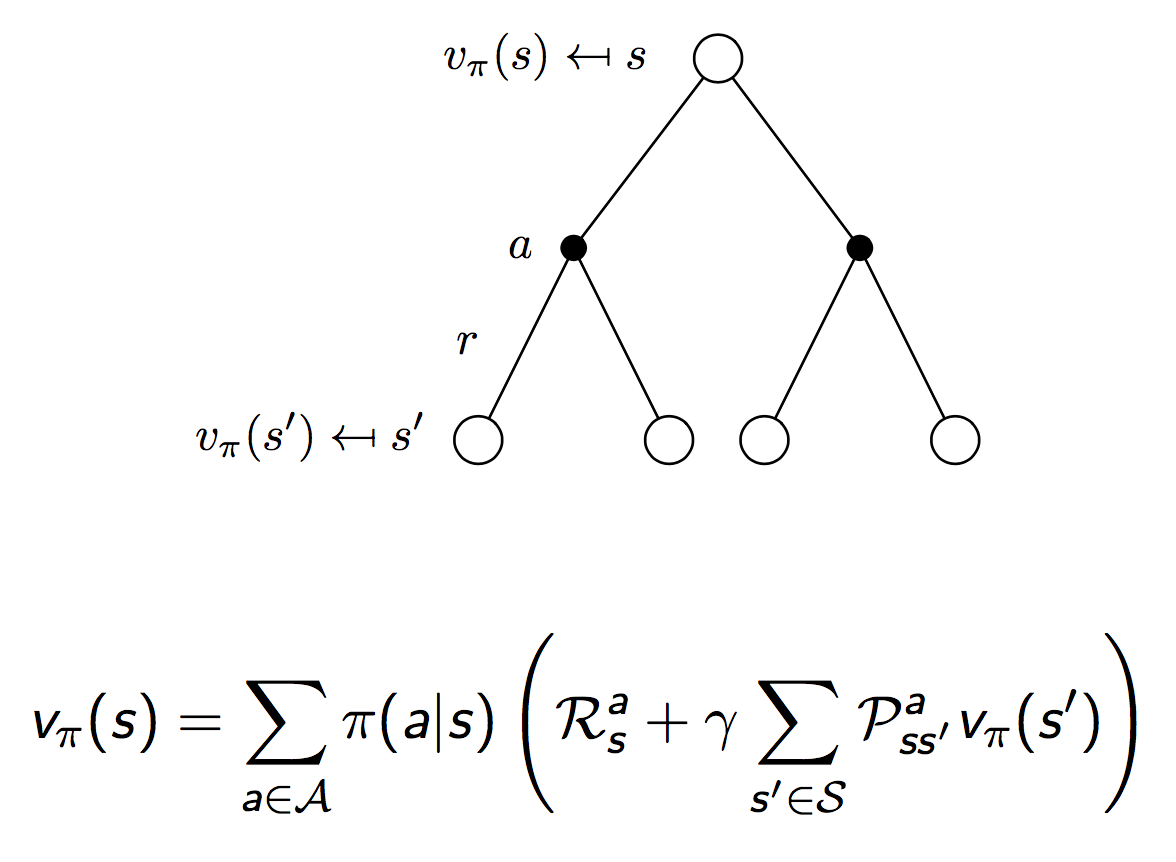

同样，相邻时刻Q函数的关系：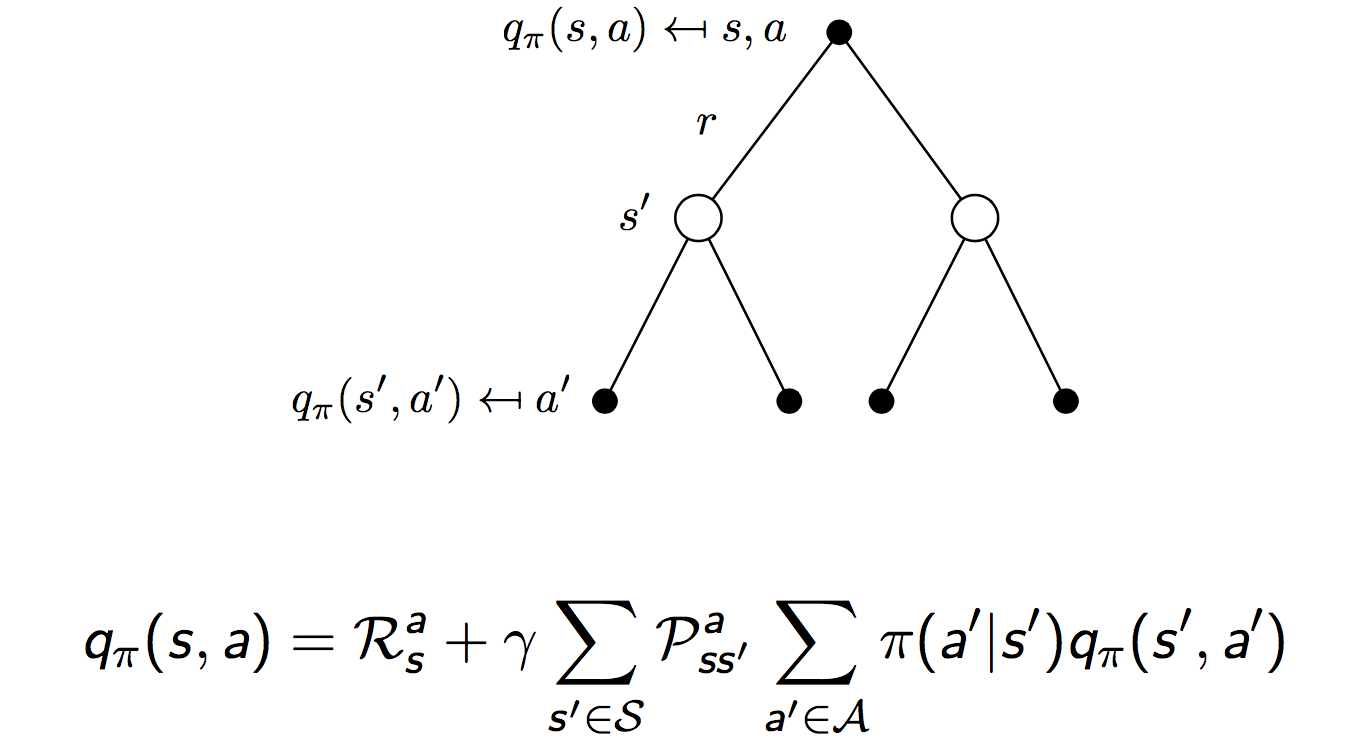

写成紧凑的矩阵形式：

$$v_\pi = R^\pi + \gamma P^\pi v_\pi$$

这个方程的解是：

$$v_\pi = (1-\gamma P^\pi)^{-1}R^\pi$$

和上面对策略函数的分解类似，我们有下面两式成立：

$$v_\pi(s) = E_\pi[R_{t+1} + \gamma v_\pi(sS_{t+1})]$$

最优值函数

最优的值函数是指在所有的策略中，使得$v_\pi(s)$取得最大值的那个，即：

$$v_\ast(s) = \max_\pi v_\pi(s)$$

最优Q函数的定义同理：

$$q_\ast(s,a) = \max_\pi q_\pi(s,a)$$

定义策略$\pi$集合上的一个偏序为

$$\pi > \pi^\prime \quad \text{if} \quad v_\pi(s) > v_{\pi^\prime}(s), \forall s$$

如果我们已经知道了最优的值函数，那么我们可以在每一步选取动作的时候，选取那个使得当前Q函数取得最大值的动作即可。这很straight forward，用数学语言表达就是：

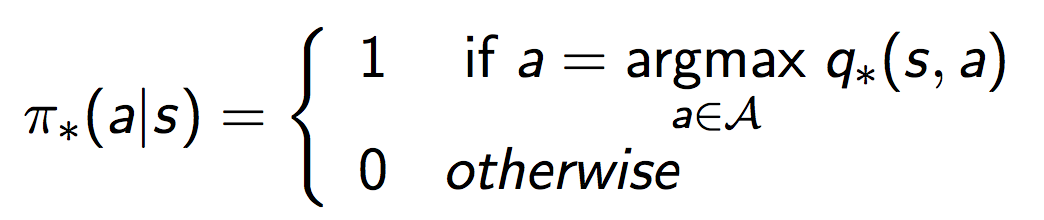
同样地，对于最优值函数，也有贝尔曼递归方程成立。下面是一个形象化的推导，和上面导出贝尔曼方程的思路是一样的。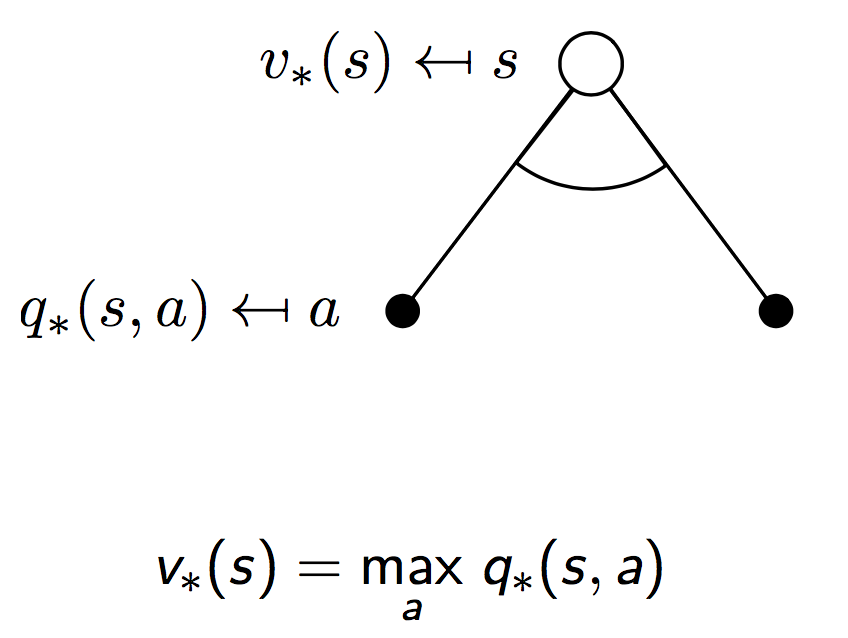

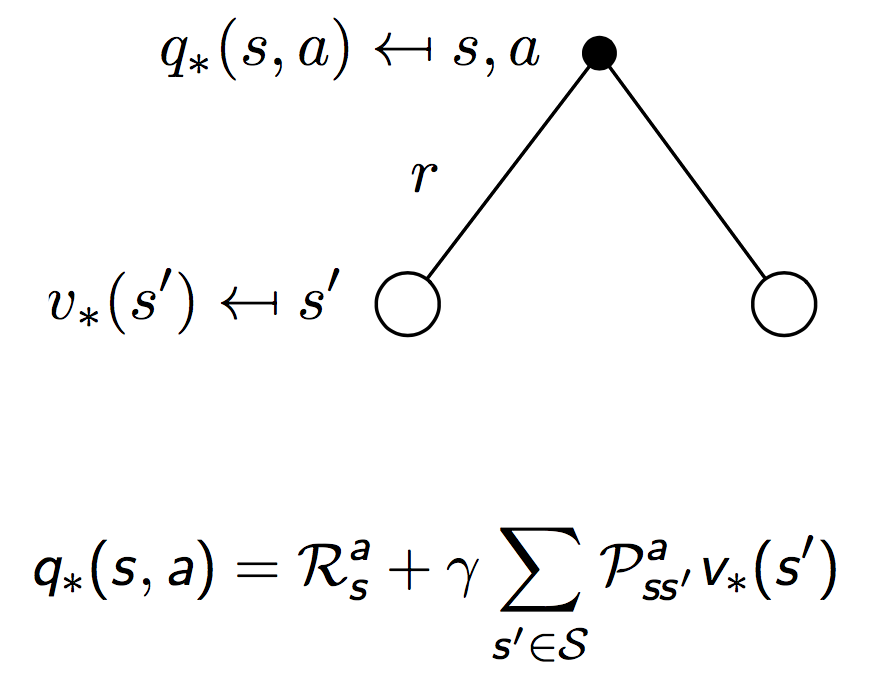
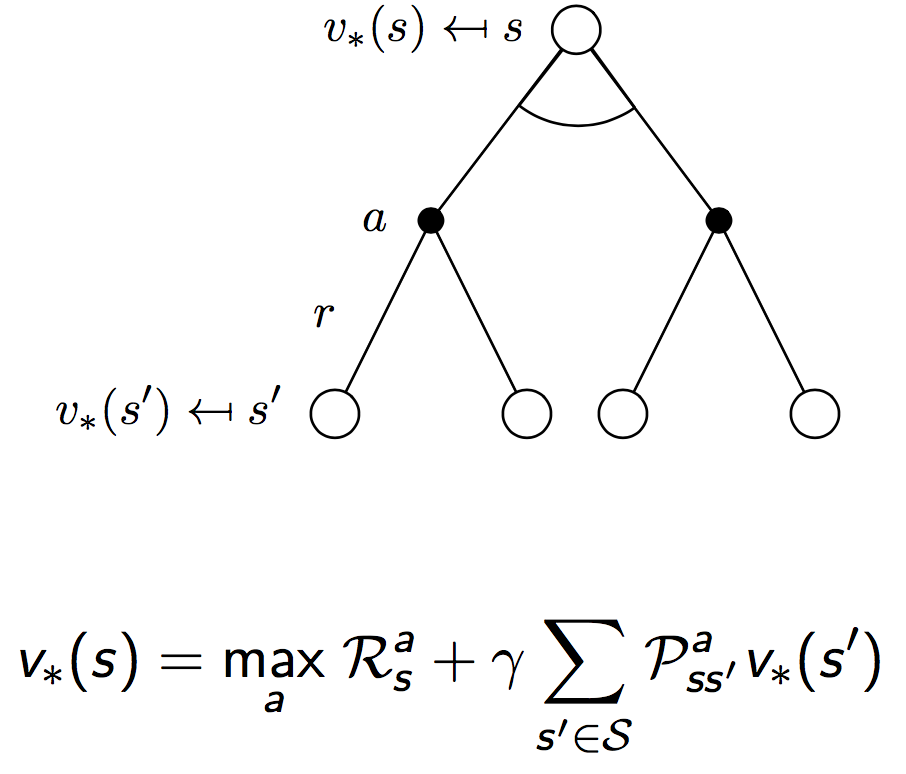
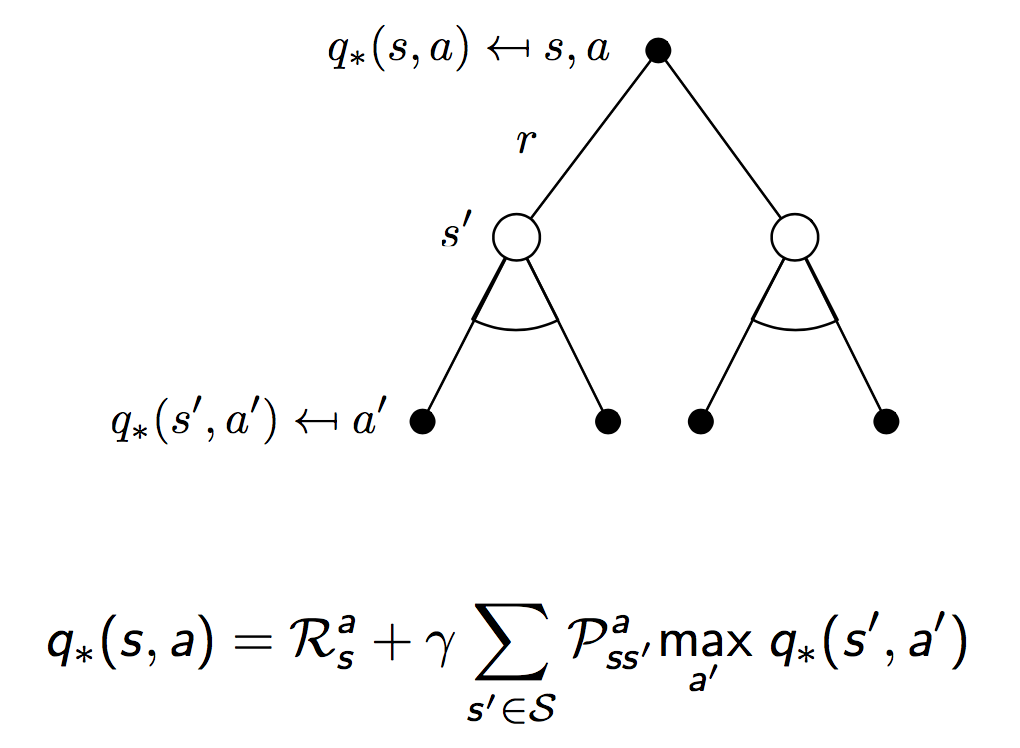
常用的求解方法包括：

• 值迭代（Value Iteration）
• 策略迭代（Policy Iteration）
• Q Learning
• Sarsa