Caffe中的BatchNorm实现

这篇博客总结了Caffe中BN的实现。

BN简介

由于BN技术已经有很广泛的应用，所以这里只对BN做一个简单的介绍。

BN是Batch Normalization的简称，来源于Google研究人员的论文：Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift。对于网络的输入层，我们可以采用减去均值除以方差的方法进行归一化，对于网络中间层，BN可以实现类似的功能。

在BN层中，训练时，会对输入blob各个channel的均值和方差做一统计。在做inference的时候，我们就可以利用均值和方法，对输入$x$做如下的归一化操作。其中，$\epsilon$是为了防止除数是$0$，$i$是channel的index。

$\hat{x_i} = \frac{x_i-\mu_i}{\sqrt{Var(x_i)+\epsilon}}$

不过如果只是做如上的操作，会影响模型的表达能力。例如，Identity Map($y = x$)就不能表示了。所以，作者提出还需要在后面添加一个线性变换，如下所示。其中，$\gamma$和$\beta$都是待学习的参数，使用梯度下降进行更新。BN的最终输出就是$y$。

$y_i = \gamma \hat{x_i} + \beta$

如下图所示，展示了BN变换的过程。

上面，我们讲的还是inference时候BN变换是什么样子的。那么，训练时候，BN是如何估计样本均值和方差的呢？下面，结合Caffe的代码进行梳理。

BN in Caffe

在BVLC的Caffe实现中，BN层需要和Scale层配合使用。在这里，BN层专门用来做“Normalization”操作（确实是人如其名了），而后续的线性变换层，交给Scale层去做。

下面的这段代码取自He Kaiming的Residual Net50的模型定义文件。在这里，设置batch_norm_param中use_global_stats为true，是指在inference阶段，我们只使用已经得到的均值和方差统计量，进行归一化处理，而不再更新这两个统计量。后面Scale层设置的bias_term: true是不可省略的。这个选项将其配置为线性变换层。

layer {
	bottom: "conv1"
	top: "conv1"
	name: "bn_conv1"
	type: "BatchNorm"
	batch_norm_param {
		use_global_stats: true
	}
}

layer {
	bottom: "conv1"
	top: "conv1"
	name: "scale_conv1"
	type: "Scale"
	scale_param {
		bias_term: true
	}
}

这就是Caffe中BN层的固定搭配方法。这里只是简单提到，具体参数的意义待我们深入代码可以分析。

BatchNorm 层的实现

上面说过，Caffe中的BN层与原始论文稍有不同，只是做了输入的归一化，而后续的线性变换是交由后续的Scale层实现的。

proto定义的相关参数

我们首先看一下caffe.proto中关于BN层参数的描述。保留了原始的英文注释，并添加了中文解释。

message BatchNormParameter {
  // If false, normalization is performed over the current mini-batch
  // and global statistics are accumulated (but not yet used) by a moving
  // average.
  // If true, those accumulated mean and variance values are used for the
  // normalization.
  // By default, it is set to false when the network is in the training
  // phase and true when the network is in the testing phase.
  // 设置为False的话，更新全局统计量，对当前的mini-batch进行规范化时，不使用全局统计量，而是
  // 当前batch的均值和方差。
  // 设置为True，使用全局统计量做规范化。
  // 后面在BN的实现代码我们会看到，这个变量默认随着当前网络在train或test phase而变化。
  // 当train时为false，当test时为true。
  optional bool use_global_stats = 1;
  
  // What fraction of the moving average remains each iteration?
  // Smaller values make the moving average decay faster, giving more
  // weight to the recent values.
  // Each iteration updates the moving average @f$S_{t-1}@f$ with the
  // current mean @f$ Y_t @f$ by
  // @f$ S_t = (1-\beta)Y_t + \beta \cdot S_{t-1} @f$, where @f$ \beta @f$
  // is the moving_average_fraction parameter.
  // BN在统计全局均值和方差信息时，使用的是滑动平均法，也就是
  // St = (1-beta)*Yt + beta*S_{t-1}
  // 其中St为当前估计出来的全局统计量（均值或方差），Yt为当前batch的均值或方差
  // beta是滑动因子。其实这是一种很常见的平滑滤波的方法。
  optional float moving_average_fraction = 2 [default = .999];
  
  // Small value to add to the variance estimate so that we don't divide by
  // zero.
  // 防止除数为0加上去的eps
  optional float eps = 3 [default = 1e-5];
}

OK。现在可以进入BN的代码实现了。阅读大部分代码都没有什么难度，下面主要结合代码讲解use_global_stats变量的作用和均值（方差同理）的计算。由于均值和方差的计算原理相近，所以下面只会详细介绍均值的计算。

SetUp

BN层的SetUp代码如下。首先，会根据当前处于train还是test决定是否使用全局的统计量。如果prototxt文件中设置了use_global_stats标志，则会使用用户给定的配置。所以一般在使用BN时，无需对use_global_stats进行配置。

这里有一个地方容易迷惑。BN中要对样本的均值和方差进行统计，即我们需要两个blob来存储。但是从下面的代码可以看到，BN一共有3个blob作为参数。这里做一解释，主要参考了wiki的moving average条目。

template <typename Dtype>
void BatchNormLayer<Dtype>::LayerSetUp(const vector<Blob<Dtype>*>& bottom,
      const vector<Blob<Dtype>*>& top) {
  BatchNormParameter param = this->layer_param_.batch_norm_param();
  moving_average_fraction_ = param.moving_average_fraction();
  // 默认根据当前是否处在TEST模式而决定是否使用全局mean和var
  use_global_stats_ = this->phase_ == TEST;
  if (param.has_use_global_stats())
    use_global_stats_ = param.use_global_stats();
  // 得到channels数量
  // 为了防止越界，首先检查输入是否为1D
  if (bottom[0]->num_axes() == 1)
    channels_ = 1;
  else
    channels_ = bottom[0]->shape(1);
  eps_ = param.eps();
  if (this->blobs_.size() > 0) {
    LOG(INFO) << "Skipping parameter initialization";
  } else {
    // 参数共3个
    this->blobs_.resize(3);
    vector<int> sz;
    sz.push_back(channels_);
    // mean 和var都是1D的长度为channels的向量
    // 因为在规范化过程中，要逐channel进行，即：
    // for c in range(channels):
    //     x_hat[c] = (x[c] - mean[c]) / std[c]
    this->blobs_[0].reset(new Blob<Dtype>(sz));
    this->blobs_[1].reset(new Blob<Dtype>(sz));
    // 这里的解释见下
    sz[0] = 1;
    this->blobs_[2].reset(new Blob<Dtype>(sz));
    for (int i = 0; i < 3; ++i) {
      caffe_set(this->blobs_[i]->count(), Dtype(0),
                this->blobs_[i]->mutable_cpu_data());
    }
  }
  // Mask statistics from optimization by setting local learning rates
  // for mean, variance, and the bias correction to zero.
  // mean 和 std在训练的时候是不需要梯度下降来更新的，这里强制把其learning rate
  // 设置为0
  for (int i = 0; i < this->blobs_.size(); ++i) {
    if (this->layer_param_.param_size() == i) {
      ParamSpec* fixed_param_spec = this->layer_param_.add_param();
      fixed_param_spec->set_lr_mult(0.f);
    } else {
      CHECK_EQ(this->layer_param_.param(i).lr_mult(), 0.f)
          << "Cannot configure batch normalization statistics as layer "
          << "parameters.";
    }
  }
}

在求取某个流数据（stream）的平均值的时候，常用的一种方法是滑动平均法，也就是使用系数$\alpha$来做平滑滤波，如下所示：

$S_t = \alpha Y_t + (1-\alpha) S_{t-1}$

上面的式子等价于：

$S_t = \frac{\text{WeightedSum}_n}{\text{WeightedCount}_n}$

其中， $\text{WeightedSum}_n = Y_t + (1-\alpha) \text{WeightedSum}_{n-1}$

$\text{WeightedCount}_n = 1 + (1-\alpha) \text{WeightedCount}_{n-1}$

而Caffe中BN的实现中，blobs_[0]和blobs_[1]中存储的实际是$\text{WeightedSum}_n$，而blos_[2]中存储的是$\text{WeightedCount}_n$。所以，真正的mean和var是两者相除的结果。即：

1 2	mu = blobs_[0] / blobs_[2] var = blobs_[1] / blobs_[2]

Forward

下面是Forward CPU的代码。主要应该注意当前batch的mean和var的求法。

template <typename Dtype>
void BatchNormLayer<Dtype>::Forward_cpu(const vector<Blob<Dtype>*>& bottom,
    const vector<Blob<Dtype>*>& top) {
  const Dtype* bottom_data = bottom[0]->cpu_data();
  Dtype* top_data = top[0]->mutable_cpu_data();
  int num = bottom[0]->shape(0);
  int spatial_dim = bottom[0]->count()/(bottom[0]->shape(0)*channels_);

  // 如果不是就地操作，首先将bottom的数据复制到top
  if (bottom[0] != top[0]) {
    caffe_copy(bottom[0]->count(), bottom_data, top_data);
  }

  // 如果使用全局统计量，我们需要先计算出真正的mean和var
  if (use_global_stats_) {
    // use the stored mean/variance estimates.
    const Dtype scale_factor = this->blobs_[2]->cpu_data()[0] == 0 ?
        0 : 1 / this->blobs_[2]->cpu_data()[0];
    // mean = blobs[0] / blobs[2]
    caffe_cpu_scale(variance_.count(), scale_factor,
        this->blobs_[0]->cpu_data(), mean_.mutable_cpu_data());
    // var = blobs[1] / blobs[2]
    caffe_cpu_scale(variance_.count(), scale_factor,
        this->blobs_[1]->cpu_data(), variance_.mutable_cpu_data());
  } else {
    // 不使用全局统计量时，我们要根据当前batch的mean和var做规范化
    // compute mean
    // spatial_sum_multiplier_是全1向量
    // batch_sum_multiplier_也是全1向量
    // gemv做矩阵与向量相乘 y = alpha*A*x + beta*y。
    // 下面式子是将bottom_data这个矩阵与一个全1向量相乘，
    // 相当于是在统计行和。
    // 注意第二个参数channels_ * num指矩阵的行数，第三个参数是矩阵的列数
    // 所以这是在计算每个channel的feature map的和
    // 结果out[n][c]是指输入第n个sample的第c个channel的和
    // 同时，传入了 1. / (num * spatial_dim) 作为因子乘到结果上面，作用见下面
    caffe_cpu_gemv<Dtype>(CblasNoTrans, channels_ * num, spatial_dim,
        1. / (num * spatial_dim), bottom_data,
        spatial_sum_multiplier_.cpu_data(), 0.,
        num_by_chans_.mutable_cpu_data());
    // 道理和上面相同，注意下面通过传入CblasTrans，指定了矩阵要转置。所以是在求列和
    // 这样，就求出了各个channel的和。
    // 上面不是已经除了 num * spatial_dim 吗？这就是求和元素的总数量
    // 到此，我们就完成了对当前batch的平均值的求解
    caffe_cpu_gemv<Dtype>(CblasTrans, num, channels_, 1.,
        num_by_chans_.cpu_data(), batch_sum_multiplier_.cpu_data(), 0.,
        mean_.mutable_cpu_data());
  }

  // subtract mean
  // gemm是在做矩阵与矩阵相乘 C = alpha*A*B + beta*C
  // 下面这个是在做broadcasting subtraction
  caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, num, channels_, 1, 1,
      batch_sum_multiplier_.cpu_data(), mean_.cpu_data(), 0.,
      num_by_chans_.mutable_cpu_data());
  caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, channels_ * num,
      spatial_dim, 1, -1, num_by_chans_.cpu_data(),
      spatial_sum_multiplier_.cpu_data(), 1., top_data);

  // 计算当前的var
  if (!use_global_stats_) {
    // compute variance using var(X) = E((X-EX)^2)
    caffe_sqr<Dtype>(top[0]->count(), top_data,
                     temp_.mutable_cpu_data());  // (X-EX)^2
    caffe_cpu_gemv<Dtype>(CblasNoTrans, channels_ * num, spatial_dim,
        1. / (num * spatial_dim), temp_.cpu_data(),
        spatial_sum_multiplier_.cpu_data(), 0.,
        num_by_chans_.mutable_cpu_data());
    caffe_cpu_gemv<Dtype>(CblasTrans, num, channels_, 1.,
        num_by_chans_.cpu_data(), batch_sum_multiplier_.cpu_data(), 0.,
        variance_.mutable_cpu_data());  // E((X_EX)^2)

    // compute and save moving average
    // 做滑动平均，更新全局统计量，这里可以参见上面的式子
    this->blobs_[2]->mutable_cpu_data()[0] *= moving_average_fraction_;
    this->blobs_[2]->mutable_cpu_data()[0] += 1;
    caffe_cpu_axpby(mean_.count(), Dtype(1), mean_.cpu_data(),
        moving_average_fraction_, this->blobs_[0]->mutable_cpu_data());
    int m = bottom[0]->count()/channels_;
    Dtype bias_correction_factor = m > 1 ? Dtype(m)/(m-1) : 1;
    caffe_cpu_axpby(variance_.count(), bias_correction_factor,
        variance_.cpu_data(), moving_average_fraction_,
        this->blobs_[1]->mutable_cpu_data());
  }

  // normalize variance
  caffe_add_scalar(variance_.count(), eps_, variance_.mutable_cpu_data());
  caffe_sqrt(variance_.count(), variance_.cpu_data(),
             variance_.mutable_cpu_data());

  // replicate variance to input size
  // 同样是在做broadcasting
  caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, num, channels_, 1, 1,
      batch_sum_multiplier_.cpu_data(), variance_.cpu_data(), 0.,
      num_by_chans_.mutable_cpu_data());
  caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, channels_ * num,
      spatial_dim, 1, 1., num_by_chans_.cpu_data(),
      spatial_sum_multiplier_.cpu_data(), 0., temp_.mutable_cpu_data());
  caffe_div(temp_.count(), top_data, temp_.cpu_data(), top_data);
  // TODO(cdoersch): The caching is only needed because later in-place layers
  //                 might clobber the data.  Can we skip this if they won't?
  caffe_copy(x_norm_.count(), top_data,
      x_norm_.mutable_cpu_data());
}

由上面的计算过程不难得出，当经过很多轮迭代之后，blobs_[2]的值会趋于稳定。下面我们使用$m_t$来表示第$t$轮迭代后的blobs_[2]的值，也就是$\text{WeightedCount}_n$，使用$\alpha$表示moving_average_fraction_，那么我们有：

$m_t = 1 + \alpha m_{t-1}$

可以求取$m_t$的通项后令$t=\infty$，可以得到，$m_{\infty}=\frac{1}{1-\alpha}$。

Backward

在做BP的时候，我们需要分情况讨论。

当use_global_stats == true的时候，BN所做的操作是一个线性变换 $BN(x) = \frac{x-\mu}{\sqrt{Var}}$ 所以 $\frac{\partial L}{\partial x} = \frac{1}{\sqrt{Var}}\frac{\partial L}{\partial y}$

对应的代码如下。其中，temp_是broadcasting之后的输入x的标准差（见上面Forward部分的代码最后），做逐元素的除法即可。

if (use_global_stats_) {
  caffe_div(temp_.count(), top_diff, temp_.cpu_data(), bottom_diff);
  return;
}

当use_global_stats == false的时候，BN所做操作虽然也是上述线性变换。但是注意，现在式子里面的$\mu$和$Var(x)$都是当前batch计算出来的，也就是它们都是输入x的函数。所以就麻烦了不少。这里我并没有推导，而是看了这篇博客，里面有详细的推导过程，写的很易懂。我将最后的结果贴在下面，对计算过程感兴趣的可以去原文章查看。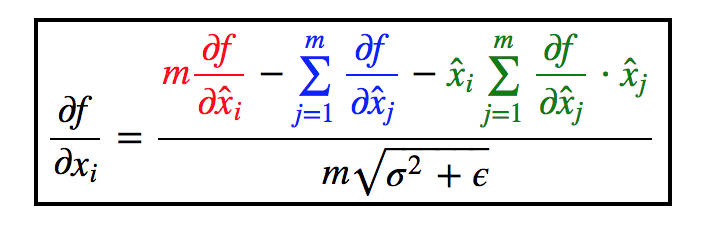

我们使用$y$来代替上面的$\hat{x_i}$，并且上下同时除以$m$，就可以得到Caffe BN代码中所给的BP式子：

$\frac{\partial f}{\partial x_i} = \frac{\frac{\partial f}{\partial y}-E[\frac{\partial f}{\partial y}]-yE[\frac{\partial f}{\partial y}y]}{\sqrt{\sigma^2+\epsilon}}$

// if Y = (X-mean(X))/(sqrt(var(X)+eps)), then
//
// dE(Y)/dX =
//   (dE/dY - mean(dE/dY) - mean(dE/dY \cdot Y) \cdot Y)
//     ./ sqrt(var(X) + eps)
//
// where \cdot and ./ are hadamard product and elementwise division,
// respectively, dE/dY is the top diff, and mean/var/sum are all computed
// along all dimensions except the channels dimension.  In the above
// equation, the operations allow for expansion (i.e. broadcast) along all
// dimensions except the channels dimension where required.

下面的代码部分就是实现上面这个式子的内容，注释很详细，要解决的一个比较棘手的问题就是broadcasting，这个有兴趣可以看一下。对Caffe中BN的介绍就到这里。下面介绍与BN经常成对出现的Scale层。

Scale层的实现

Caffe中将后续的线性变换使用单独的Scale层实现。Caffe中的Scale可以根据需要配置成不同的模式：

当输入blob为两个时，计算输入blob的逐元素乘的结果（维度不相同时，第二个blob可以做broadcasting）。
当输入blob为一个时，计算输入blob与一个可学习参数gamma的按元素相乘结果。
当设置bias_term: true时，添加一个偏置项。

用于BN的线性变换的计算方法很直接，这里不再多说了。