CS131-描述图像的特征(Harris 角点)

feature是对图像的描述。比如，图像整体灰度值的均值和方差就可以作为feature。如果我们想在一副图像中检测足球时，可以使用滑动窗方法，逐一检查窗口内的灰度值分布是否和一张给定的典型黑白格子足球相似。可想而知，这种方法的性能一定让人捉急。而在image matching问题中，常常需要将不同视角的同一目标物进行matching，进而计算相机转过的角度。这在SLAM问题中很有意义。如下图所示，同一处景观，在不同摄影师的镜头下，不仅视角不同，而且明暗变化也有很多差别，右侧的图暖色调更浓。这也告诉我们，上面提到的只使用全局图像灰度值来做feature的做法有多么不靠谱。

那么，让我们脱离全局特征，转而将注意力集中在局部特征上。这是因为使用局部特征能够更好地处理图像中的遮挡、变形等情况，而且我们的研究对象常常是图像中的部分区域而不是图像整体。更特殊地，在这一讲中，我们主要探究key point作为local feature的描述，并介绍Harris角点检测方法。在下一节中介绍SIFT特征。

Harris角点

角点，即corner，和edge类似，区别在于其在两个方向上都有较为剧烈的灰度变化（而edge只在某一个方向上灰度值变化剧烈）。如图所示。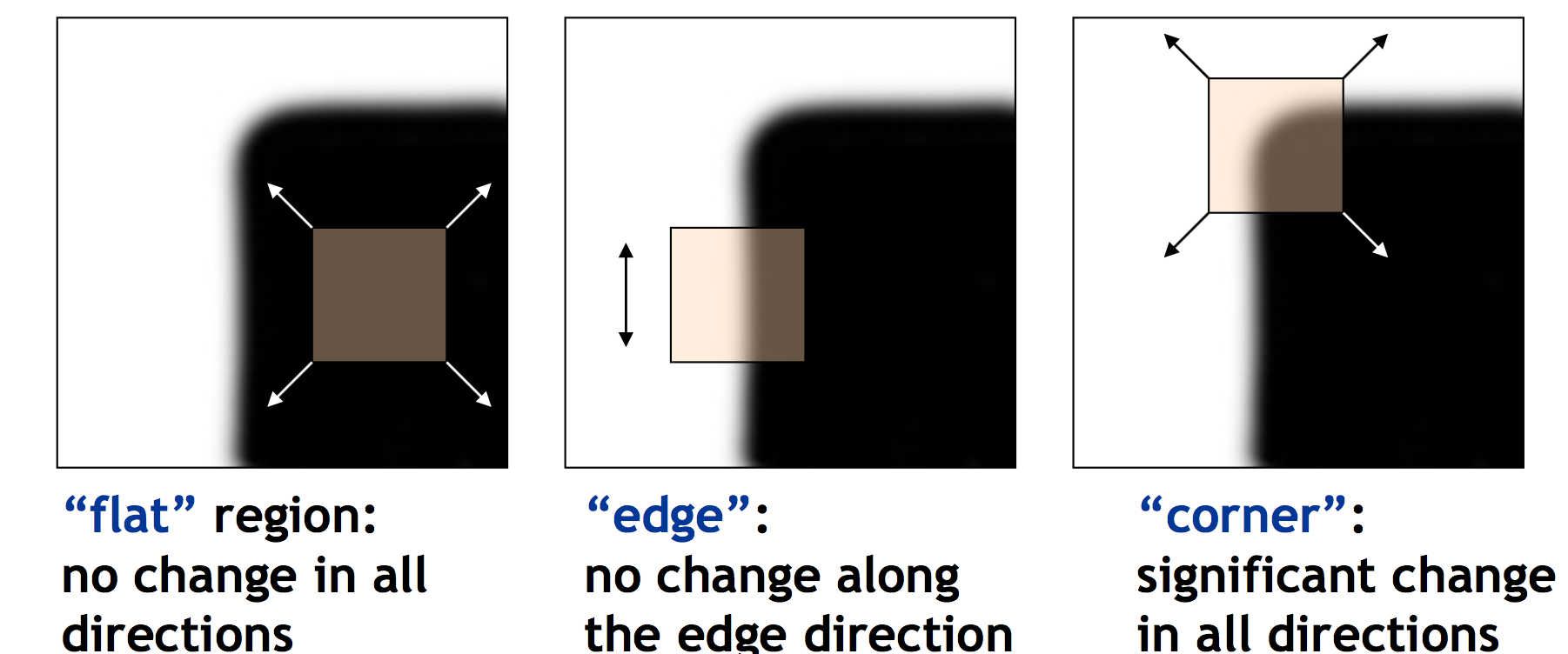

Harris角点得名于其发明者Harris，是一种常见的角点检测方法。
给定观察窗口大小，计算平移后窗口内各个像素差值的加权平方和，如下式。

$$E(u,v) = \sum_x\sum_yw(x,y)[I(x+u, y+v) - I(x,y)]^2$$

其中，窗口加权函数$w$可以取做门限函数或gaussian函数。如图所示。

使用泰勒级数展开，并忽略非线性项，我们有

$$I(x+u,y+v) = I(x,y) + I_x(x,y)u+I_y(x,y)v$$

所以上式可以写成（线性二次型写成了矩阵形式），

$$E(u,v) = \sum_{x,y}w(I_xu+I_yv)^2 = \begin{bmatrix}u&v\end{bmatrix}M\begin{bmatrix}u\\\\v\end{bmatrix}$$

其中，

$$M = w\begin{bmatrix}I_x^2& I_xI_y\\\\I_xI_y&I_y^2\end{bmatrix}$$

当使用门限函数时，权值$w_{i,j} = 1$，则，

$$M = \begin{bmatrix}\sum I_xI_x& \sum I_xI_y\\\\\sum I_xI_y&\sum I_yI_y\end{bmatrix} = \sum \begin{bmatrix}I_x \\\\I_y\end{bmatrix}\begin{bmatrix}I_x &I_y\end{bmatrix}$$

当corner与xy坐标轴对齐时候，如下图所示。由于在黑色观察窗口内，只有上侧和左侧存在边缘，且在上边缘，$I_y$很大，而$I_x=0$，在左侧边缘，$I_x$很大而$I_y = 0$，所以，矩阵

$$M = \begin{bmatrix}\lambda_1 & 0 \\\\ 0&\lambda_2 \end{bmatrix}$$

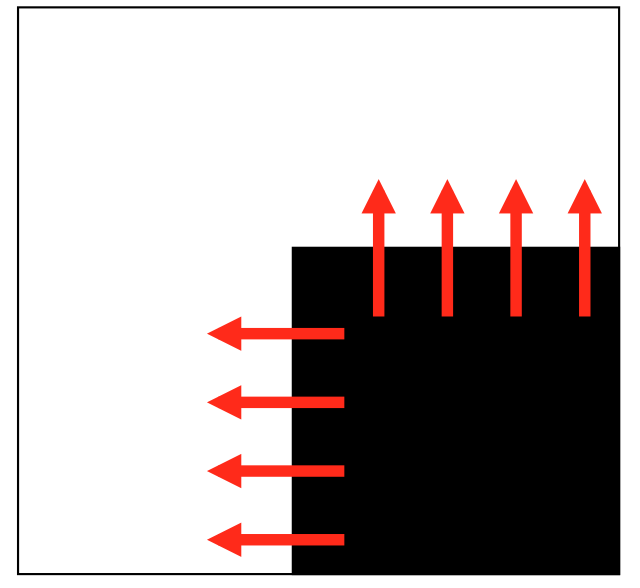
当corner与坐标轴没有对齐时，经过旋转变换就可以将其转换到与坐标轴对齐的角度，而这种旋转操作可以使用矩阵的相似化来表示（其实是二次型的化简，可以使用合同变换，而旋转变换的矩阵是酉矩阵，转置即为矩阵的逆，所以也是相似变换）。也就是说，矩阵$M$相似于某个对角阵。

$$M = R^{-1}\Sigma R, \text{其中}\Sigma = \begin{bmatrix}\lambda_1&0\\\\0&\lambda_2\end{bmatrix}$$

所以，可以根据下面这张图利用矩阵$M$的特征值来判定角点和边缘点。当两个特征值都较大时为角点；当某个分量近似为0而另一个分量较大时，可以判定为边缘点（因为某个方向的导数为0）；当两个特征值都近似为0时，说明是普通点（flat point）。（课件原图如此，空缺的问号处应分别为$\lambda_1$和$\lambda_2$）。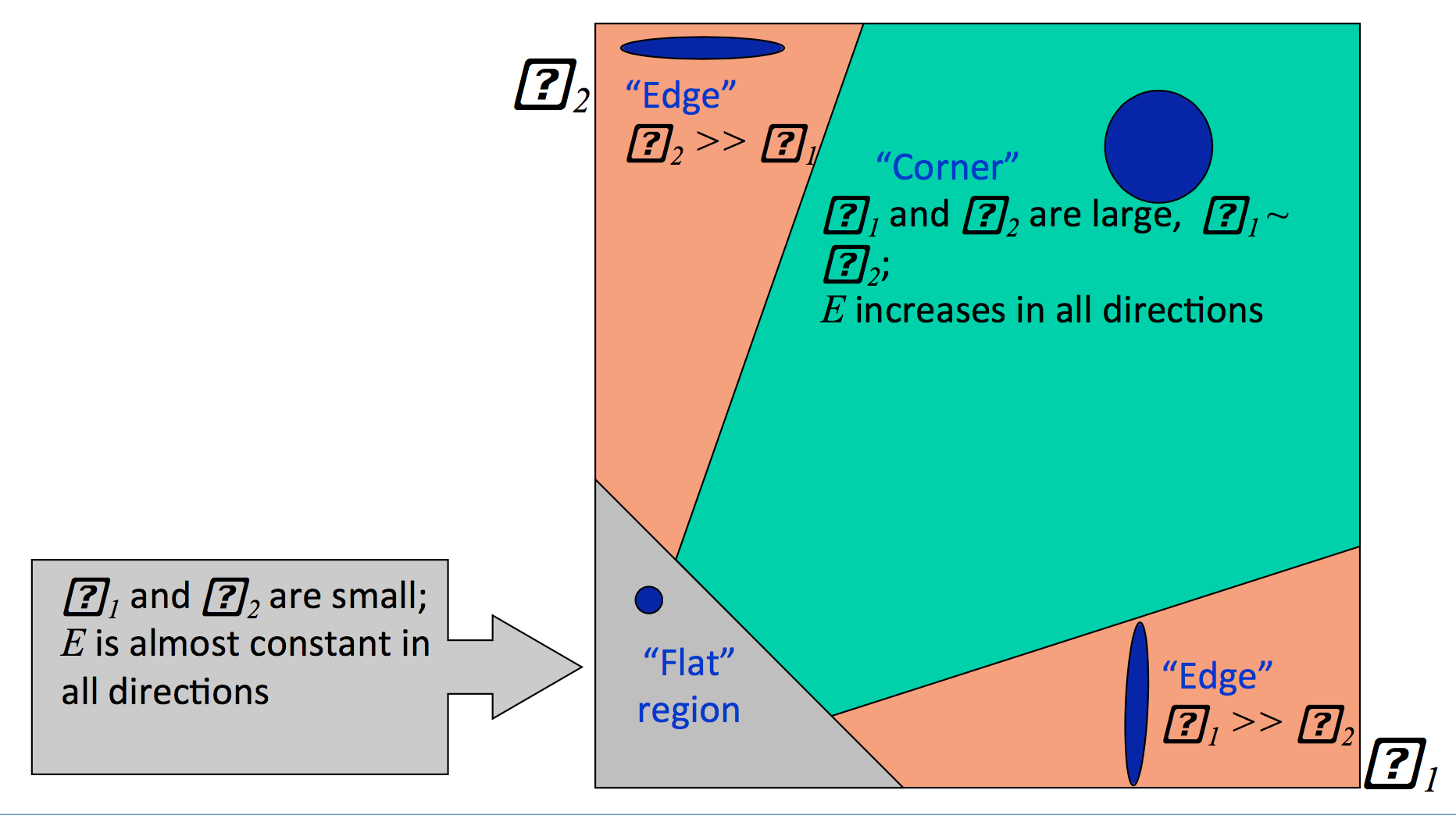

然而矩阵的特征值计算较为复杂，所以使用下面的方法进行近似计算。

$$\theta = \det(M)-\alpha\text{trace}(M)^2 = \lambda_1\lambda_2-\alpha(\lambda_1+\lambda_2)^2$$

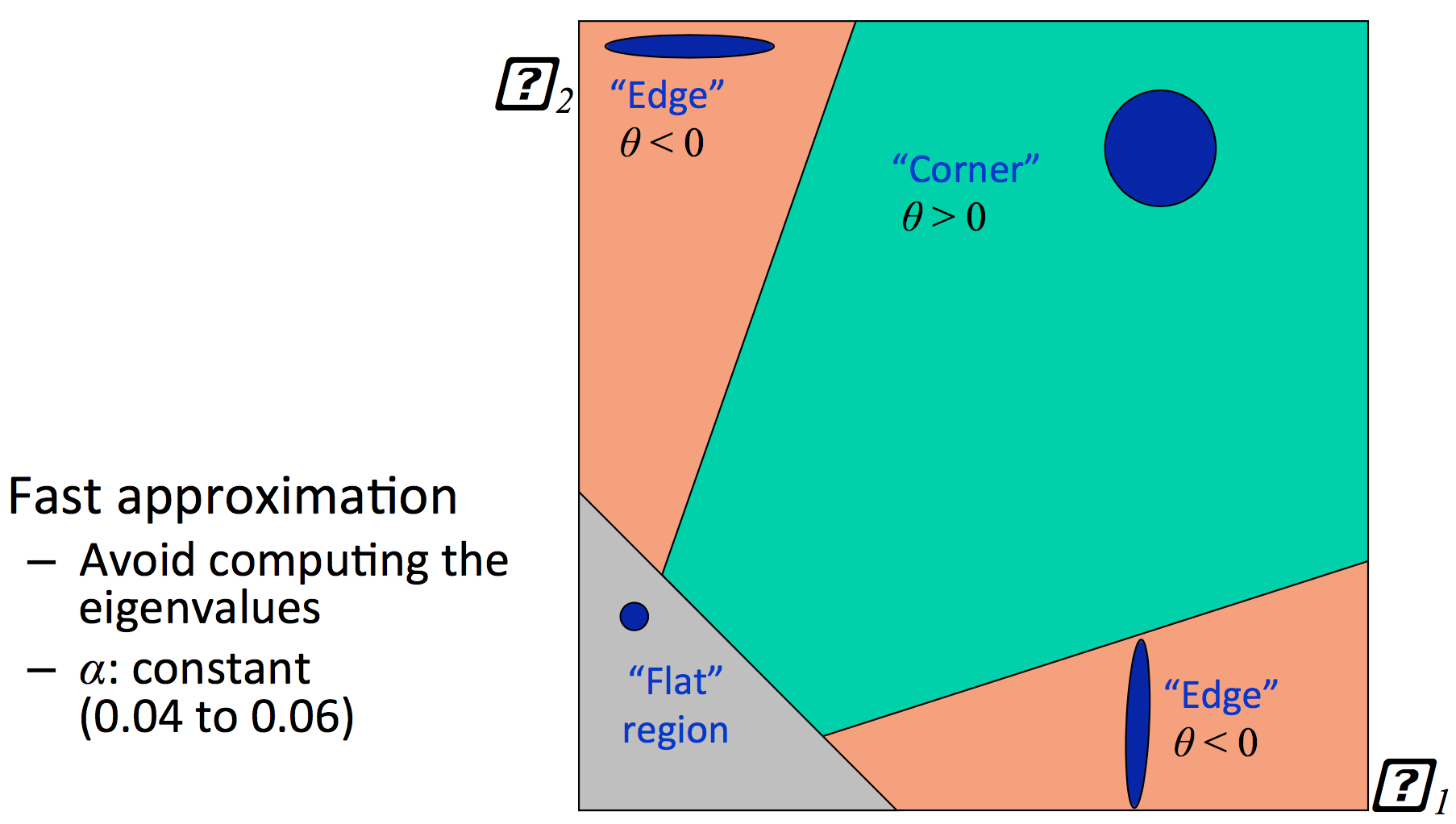
为了减弱噪声的影响，常常使用gaussian窗函数。如下式所示：

$$w(x,y) = \exp(-(x^2+y^2)/2\sigma^2)$$